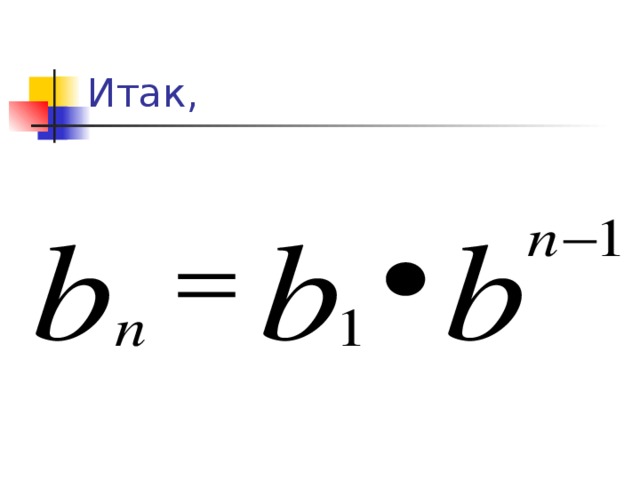Геометрическая прогрессия

Тип урока: усвоение новых знаний и первичное закрепление.

Цель урока: Формирование понятия геометрической прогрессии через понятие арифметической прогрессии, используя методы сопоставления и противопоставления. Познакомить со свойствами геометрической прогрессии и формулой n-го члена. Закрепить полученные знания на примерах решения задач.

Задачи урока:

Обучающие:

• ввести понятие геометрической прогрессии;

• развитие общеучебных умений и навыков;

  Развивающие:

• работа по овладению учебно-интеллектуальных умений (сравнение, обобщение, исследовательские);

• расширение эрудиции по предмету;

  Воспитательные:

• создание комфортной атмосферы на уроке;

• привитие навыков самооценки;

• привитие интереса к предмету.

  Содержание урока:

1. Организационный момент.
2. Самостоятельная работа с проверкой в классе. Её цель проверить домашнее задание и создать проблемную ситуацию (задание 4).
3. Организация изучения понятия геометрической прогрессии и введение формулы n-го члена геометрической прогрессии.
4. Первичное применение знаний и умений.
5. Подведение итогов работы на уроке и домашнее задание.

Средства обучения:

• < >

  мультимедийный проектор,

• < >

  раздаточный материал (2 карточки с заданиями самостоятельной работы и таблицы, количество которых равно количеству учеников в классе).

  Ход урока

  Перед уроком на экране слайд № 1. На перемене каждому ученику раздается чистый тетрадный лист.

  1. Организационный момент. Учитель сообщает классу тему урока, цель и план урока. На экране по очереди показываются слайды № 2,3,4

  2. Самостоятельная работа с проверкой в классе. В начале урока вы напишите самостоятельную работу. Я вызову двух учеников на решение самостоятельной работы к доске, а остальные будут решать на месте на листочках. В конце работы я попрошу вас перенести в тетрадь только ответы. Затем листочки сдаем и проверяем решения и ответы у учеников у доски. На решение самостоятельной работы отводится 8 минут, на 9-ой минуте переносим ответы в тетрадь.

  (Два ученика выходят к доске, им выдаются карточки с самостоятельной работой разного варианта. Они решают на “крыльях” доски, так чтобы ученики класса не видели решения). На экране слайд № 5 (На экран выводится текст самостоятельной работы. Учитель прочитывает задания.) Самостоятельная работа:

  1 вариант

1. Найдите тридцать второй член арифметической прогрессии, если первый член 65 и разность -2.
2. Найдите сумму десяти первых членов арифметической прогрессии, если а = 3n-1, n – натуральное число.
3. Найдите сумму семи первых членов арифметической прогрессии 8;4;0;…
4. Продолжите числовую последовательность, записав еще 2 члена: 1;2;4;… 2 вариант
5. Найдите двадцать третий член арифметической прогрессии, если первый член -9 и разность 4.
6. Найдите сумму десяти первых членов арифметической прогрессии, если а = 4n+2, n – натуральное число.
7. Найдите сумму семи первых членов арифметической прогрессии -5;-3;-1;…
8. Продолжите числовую последовательность, записав еще 2 члена: -2;6;-18;…

Время вышло переносим ответы в рабочую тетрадь и листочки сдаем. (Ученики переносят ответы в тетрадь и сдают листочки с решением. Ребята у доски открывают решения и на экране появляются ответы – слайд № 6.Ученики сверяют ответы и проверяют решения ребят у доски. Ученики, которые решали у доски получают оценки.) Поднимите руки,те ребята которые справились со всеми заданиями?Вы получате-5. Теперь те кто не справился с одним заданием? Вы получаете-4. Молодцы! На следующем уроке вам выдадут листочки с оценками и каждый узнает свою оценку.

3. Изучение нового материала. На экране слайд № 7. Обратите внимание на 4-ое задание самостоятельной работы. Каким образом вы продолжили последовательность? (Ученики отвечают.) Слайд № 8. То есть каждый следующий член равен произведению предыдущего на некоторое одно и то же число. Такая числовая последовательность в математике называется геометрической прогрессией. Слайд № 9.

С геометрической прогрессией, которую получили в первом веке, связана интересная легенда. Слайд№ 10. По преданию, шахматы были изобретены в пятом веке до нашей эры в Индии. Индусский царь был так восхищен игрой, что решил отблагодарить изобретателя шахмат. Который, в свою очередь,попросил следующую награду: выдать ему за первую клетку шахматной доски одно пшеничное зерно, за вторую клетку – 2 пшеничных зерна, за третью – 4,за четвертую – 8 зерен, за пятую – 16 зерен и т.д. до64-й клетки доски, т.е. за каждую следующую клетку доски следует выдавать в 2 раза больше, чем за предыдущую. Царь был не доволен просьбой, т.к.считал, что изобретатель, прося столь ничтожную награду, оскорбляет его. Слайд № 11.

И тогда придворный математик стал считать,сколько зерна должен получить изобретатель. Для того чтобы подсчитать величину награды, мы должны сложить зерна, лежащие на всех клеточках доски, т.е. найти сумму, которую видите на слайде.Слайд № 12.

Когда подсчитали сумму зерен, то количества оказалось очень большое число. Какое? Слайд № 13.Вы узнаете немного позже, когда познакомитесь с формулой суммы n первых членов геометрической прогрессии. Но такого количества зерен нет ни у какого царя, и просьбу изобретателя выполнить невозможно. А сегодня мы познакомимся с понятием геометрической прогрессии. Откройте тетради запишите число и тему урока. (В это время учитель раздает каждому заготовленную таблицу (см.приложение).) Теперь поработаем по таблице. Слайд№ 14.

Прочитайте определение арифметической прогрессии (появляется на слайде) и сформулируйте определение геометрической прогрессии. (Ученики отвечают и по щелчку на слайде появляется определение геометрической прогрессии.) А теперь запишем в таблицу определение геометрической прогрессии. Слайд №15.

Познакомимся с названием числа q. Смотрите слайд. Следующий пункт в таблице: обозначение,смотрим слайд и записываем. Слайд № 16.

Какие значения могут принимать первый член и знаменатель геометрической прогрессии? (Ученики отвечают.) Смотрим слайд. Слайд № 17.

Давайте выведем рекуррентную формулу? Слайд №18.

(На слайде сначала появляется рекуррентная формула арифметической прогрессии. Ученики называют рекуррентную формулу геометрической прогрессии. И по щелчку на слайде появляется эта формула. ) А как найти знаменатель геометрической прогрессии? (Ученики рассуждают.) Слайд № 19.

(На слайде сначала появляется как найди d.Ученики по аналогии догадываются, как найти q и на слайде появляется формула). Слайд № 20.

Используя рекуррентную формулу, можно получить формулу n-го члена. Рассмотрим геометрическую прогрессию со знаменателем q. (Ученики догадываются и появляются слайд.) Слайд № 21.

Запишем формулу в таблицу. Слайд № 22.

Записывают в тетрадь. Слайд № 23.

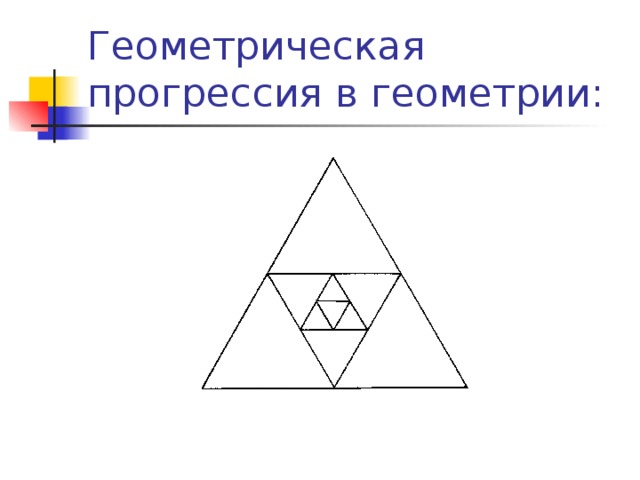
Ранее видели, что название арифметической прогрессии связано с особым свойством членов этой прогрессии. Название геометрической прогрессии также связано со свойством её членов.Итак, квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов, смотрим на слайд. Извлекая квадратный корень из обеих частей этого равенства, получим что для любых трех последовательных членов геометрической прогрессии выполняется равенство на слайде. А число, которое получилось в правой части равенства называется средним геометрическим двух чисел. Итак, запишем характеристическое свойство. В таблице остались формулы суммы nпервых членов геометрической прогрессии, вы их запишите на другом уроке. Геометрическая прогрессия применяется во многих областях.Например, в экономике (вычисление вклада,положенного под некоторый процент), в биологии(размножение микроорганизмов), в геометрии, в физике, в химии и т.д. Посмотрите, как применение геометрической прогрессии в геометрии. Слайд №24. В правильный треугольник, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Рассмотрим длины сторон этих треугольника. (Ученики рассуждают и отвечают.) Так как сторона каждого нового треугольника является средней линией предыдущего треугольника, то если сторона первого треугольника – а, второго - 1/2 а, третьего- 1/4 а, четвертого - 1/8 а и т.д. Таким образом, длины сторон образуют геометрическую прогрессию со знаменателем - 1/2.

Переходим к решению задач.

Слайд № 25.

4. Первичное применение знаний и умений.Слайд № 26.

Задача № 1. Найдите первые 5 членов геометрической прогрессии, если первый член -2, а знаменатель -0.5. (Решение пишется на доске. Если кто-то из учеников решит раньше, то на слайде выводится ответ и открывается слайд с новой задачей.)

Ответ: -2; 1; -0,5; 0,25; - 0,125

Переходим к следующей задаче, о которой сегодня уже говорили: Слайд № 27.

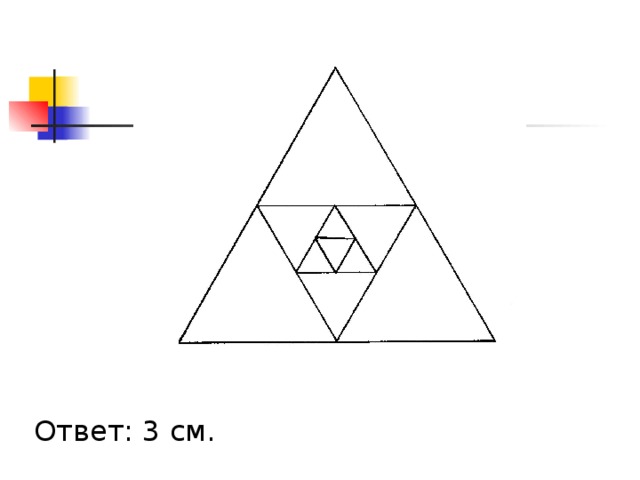
Задача № 2. В правильный треугольник,сторона которого равна 16 см, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр пятого треугольника. Слайд № 28. (Решение пишется на доске. Если кто-то из учеников решит раньше, то на слайде выводится ответ и открывается слайд с новой задачей.)

Ответ: 3 см Слайд № 29.

Задача № 3. Найдите знаменатель геометрической прогрессии, если ее четвертый член 25, а шестой член 16.(Решить двумя способами: 1)использовать характеристическое свойство;2)составить систему уравнений с двумя переменными). (Обсудить решения с учениками и двух человек вызвать к доске.)

Ответ:

Слайд № 30.

Задача № 4.Между числами и 27 вставьте четыре числа,чтобы получилась геометрическая прогрессия.Найдите эти числа. (Решение пишется на доске. Если кто-то из учеников решит раньше, то на слайде выводится ответ и открывается слайд с новой задачей.)

Ответ: ; 1; 3; 9.

Слайд № 31.

Задача № 5.Дана геометрическая прогрессия ( ),в которой и

Найти первый член геометрической прогрессии.

Ответ: 12 или

(Эту задачу можно дать на самостоятельное решение ученикам, которые решает быстрее класса.Количество может быть определено самим учителем.) (Когда ученики решат последнюю задачу,нужно подвести итог урока.)

5. Итог урока

Слайд № 32. Давайте посмотрим на таблицу,которую заполняли во время объяснения нового материала. Назовите общее и различное в определении и свойствах арифметической и геометрической прогрессии? Где применяется геометрическая прогрессия? (Ученики отвечают.Учитель оценивает работу учеников, кому-то ставит оценку за урок.)

Слайд № 33.

Домашнее задание: придумать задачу,где использовалась бы геометрическая прогрессия. Слайд № 34. На этом наш урок заканчивается. Всем спасибо! До свидания!

Приложения к уроку

Таблица

Прогрессия

Aарифметическая прогрессия

Геометрическая прогрессия

1. Определение.

Числовая последовательность, каждый член, которой, начиная со второго равен предшествующему члену сложенному с некоторым одним и тем же числом d, d – называется разностью арифметической прогрессии

2. Обозначение.

3. Допустимые значения.

- любые

4. Рекуррентная формула.

5. Нахождение

разности

знаменателя

6. Формула n-го члена.

7. Характеристическое свойство.

8. Формулы суммы n первых членов.