| №урока | Тема урока | Тип урока | Требования к уровню подготовки | Вид контроля | Д/з | ДАТА |
| план. | факт. |
|
| Повторение курса алгебры 7-9 классов |
|
|
| 1 | Нахождение процентов данного числа | Применение знаний и умений | Знать определение процента. Уметь: - записывать десятичные дроби в виде процентов и наоборот; - находить несколько процентов от величины. | Фронтальный и инди-видуальный опрос |
|
|
|
| 2 | Нахождение числа по его процентам | Применение знаний и умений | Знать определение процента. Уметь: - записывать десятичные дроби в виде процентов и наоборот; - находить величину по её проценту. | Фронтальный и инди-видуальный опрос |
|
|
|
| 3 | Нахождение процентного отношения чисел | Применение знаний и умений | Знать определение процента. Уметь: - записывать десятичные дроби в виде процентов и наоборот; - выражать часть величины в процентах. | Фронтальный и инди-видуальный опрос, само-стоятельная работа |
|
|
|
| 4 | Решение задач на части | Применение знаний и умений | Знать понятие части. Уметь решать задачи на части. | Фронтальный и инди-видуальный опрос |
|
|
|
| 5 | Практический расчёт, оценка и прикидка | Применение знаний и умений | Знать и уметь в ответе на эти задачи надо написать целое число, при этом нужно подумать, в большую или меньшую сторону округлять результат вычислений. | Фронтальный и инди-видуальный опрос |
|
|
|
| 6 | Практический расчёт, оценка и прикидка | Применение знаний и умений | Фронтальный и инди-видуальный опрос |
|
|
|
| 7 | Практический расчёт, оценка и прикидка | Применение знаний и умений | Фронтальный и инди-видуальный опрос |
|
|
|
| 8 | Практический расчёт, оценка и прикидка. Самостоятельная работа | Комбинированный | Фронтальный и индиви-дуальный опрос, само-стоятельная работа |
|
|
|
| 9 | Решение линейных уравнений | Применение знаний и умений | Знать определение линейного уравнения с одной переменной. Уметь: - решать уравнения с одной переменной; решать уравнения вида 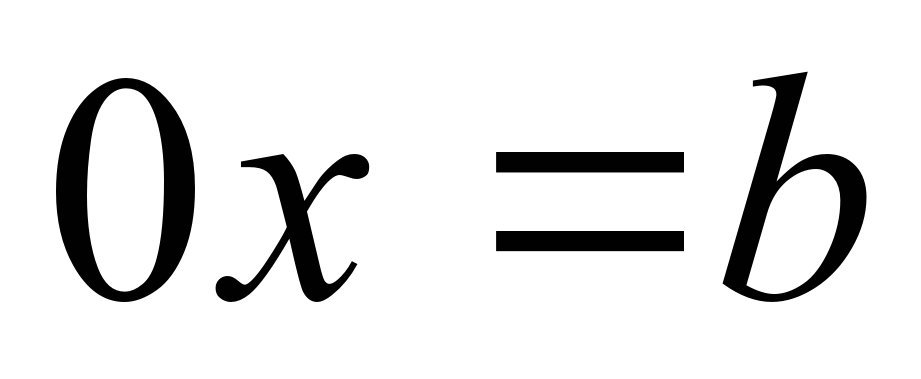 и и 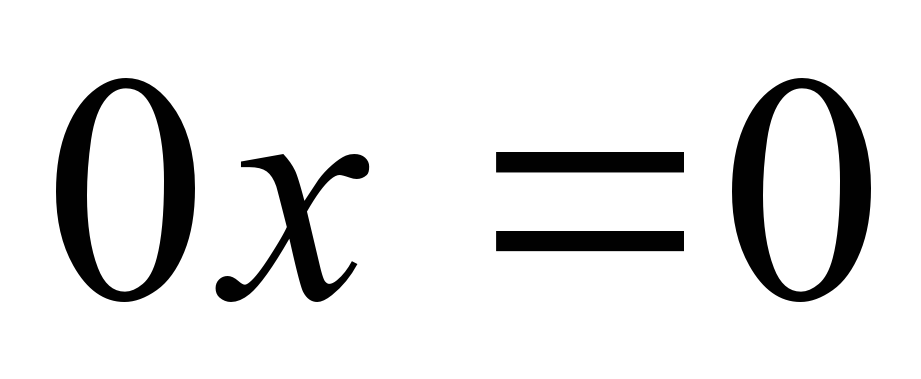 ; - выбирать способ решения уравнений. ; - выбирать способ решения уравнений. | Фронтальный и инди-видуальный опрос |
|
|
|
| 10 | Чтение графиков | Применение знаний и умений | Иметь представление о графиках. Уметь определять: - наибольшее или наименьшее зна-чение некоторой величины; - разность между наибо-льшим и наименьшим значениями; - момент времени, когда величина примет какое-то значение; - ответ на другой, подобный этим вопрос | Фронтальный и инди-видуальный опрос |
|
|
|
| 11 | Чтение диаграмм | Применение знаний и умений | Иметь представление о круговых и столбчатых диаграммах. Уметь строить столбчатые диаграммы по условиям текстовых задач. | Фронтальный и индиви-дуальный опрос |
|
|
|
| 12 | Чтение графиков и диаграмм | Применение знаний и умений | Уметь: - определять по графику значение одной величины по заданному значению другой; -анализировать изменение одной величины в зависимости от другой; - строить столб-чатые диаграммы по условиям текстовых задач. | Фронтальный и инди-видуальный опрос, само-стоятельная работа |
|
|
|
| 13 | Расчёты в повседневной жизни. Работа с таблицами | Применение знаний и умений | Уметь пользоваться таблицами. Знать: - если нужно выбрать наименьшее или наиболь-шее число, то при сравнении можно сначала сделать прикидку, а потом вычислять до конца только подходя-щий вариант; - если кто-то идёт быстрее, то его ско-рость больше; - если два объекта вышли одновременно, а именно, а один из них пришёл позже, то его время в пути больше. | Фронтальный и инди-видуальный опрос |
|
|
|
| 14 | Работа с таблицами. Расчёты в повседневной жизни | Применение знаний и умений | Фронтальный и инди-видуальный опрос |
|
|
|
| 15 | Работа с таблицами. Расчёты в повседневной жизни | Применение знаний и умений | Фронтальный и индиви-дуальный опрос |
|
|
|
| 16 | Самостоятельное решение заданий КИМов по теме «Расчёты в повседневной жизни. Работа с таблицами» | Комбинированный | Тест |
|
|
|
| 17 | Преобразование целого выражения в многочлен, используя формулы сокращённого умножения | Применение знаний и умений | Знать определение линейного уравнения с одной пере-менной. Уметь: - решать уравнения с одной переменной; решать уравнения вида 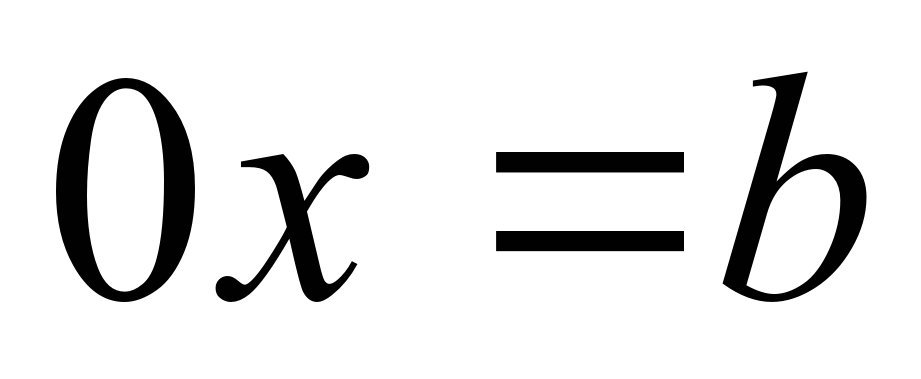 и и 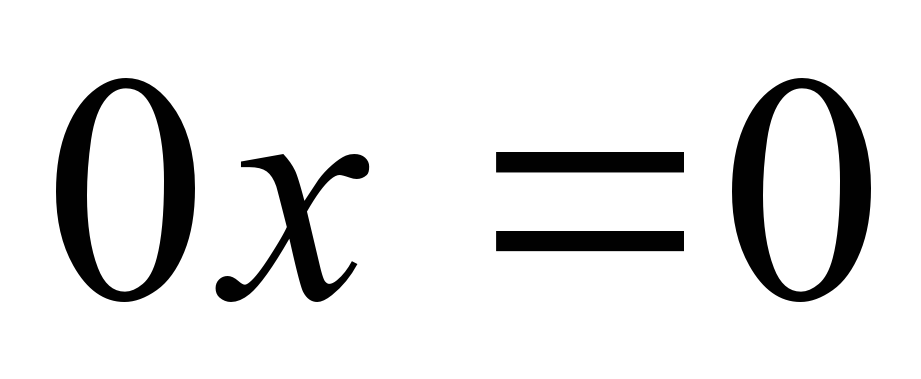 | Фронтальный и инди-видуальный опрос |
|
|
|
| 18 | Решение систем линейных уравнений | Применение знаний и умений | Уметь: - решать системы линейных уравнений способом подстановки и способом сложения; - графи-чески решать системы линейных уравнений и выяснять, сколько решений имеет система уравнений. | Фронтальный и инди-видуальный опрос |
|
|
|
| 19 | Решение квадратных уравнений | Применение знаний и умений | Уметь решать квадратные уравнения по формуле и с помощью теоремы Виета. | Фронтальный и инди-видуальный опрос |
|
|
|
| 20 | Решение систем квадратных уравнений | Применение знаний и умений | Знать системы двух уравнений второй степени с двумя переменными и методы их решения. Уметь решать системы, содержащие одно уравне-ние первой, а другое — второй степени, системы двух уравнений второй степени с двумя переменными. | Фронтальный и инди-видуальный опрос |
|
|
|
| 21 | Решение дробно-рациональных уравнений | Применение знаний и умений | Знать понятие дробно-рационального и уметь решать их. | Фронтальный и инди-видуальный опрос |
|
|
|
| 22 | Решение линейных и дробно-рациональных уравнений | Комбинированный | Уметь: - решать линейные уравнения с одной перемен-ной; - решать системы линейных уравнений способом подстановки и способом сложения; - решать квадрат-ные уравнения и неполные квадратные уравнения; - решать системы, содержащие одно уравнение первой, а другое — второй степени, системы двух уравнений второй степени с двумя переменными. | Фронтальный и инди-видуальный опрос, самостоятельная работа |
|
|
|
|
| Повторение планиметрии |
|
|
| 23 | Соотношения в прямоугольном треугольнике | Применение знаний и умений | Знать соотношения между сторонами и углами прямо-угольного треугольника. Уметь решать прямоугольные треугольники, используя определение синуса, косинуса, тангенса острого угла. | Фронтальный и инди-видуальный опрос |
|
|
|
| 24 | Соотношения в прямоугольном треугольнике | Комбинированный | Фронтальный и инди-видуальный опрос, само-стоятельная работа |
|
|
|
| 25 | Высоты в прямоугольном треугольнике | Применение знаний и умений | Знать о том, что: -в прямоугольном треугольнике две высоты совпадают с катетами; - третья высота, прове-дённая из вершины прямого угла, делит треугольник на два прямоугольных треугольника, углы которых равны соответственно углам исходного треугольника и уметь это применять при решении задач. | Фронтальный и инди-видуальный опрос |
|
|
|
| 26 | Тригонометрические функции тупого угла | Применение знаний и умений | Знать о том, что синусы смежных углов равны, косинусы противоположны, тангенсы также противоположны и уметь это применять при решении задач. | Фронтальный и инди-видуальный опрос |
|
|
|
| 27 | Равнобедренный треугольник | Применение знаний и умений | Знать: - определение равнобедренного и равностороннего треугольников; - формулировки теорем об углах при основании равнобедренного треугольника и медиане равнобедренного треугольника, проведённой к основанию. Уметь: - строить и распознавать медианы, высоты и биссектрисы треугольника; - решать задачи, используя изученные свойства равнобедренного треугольника. | Фронтальный и инди-видуальный опрос |
|
|
|
| 28 | Соотношения между сторонами и углами треугольника | Комбинированный | Знать формулировки теорем о соотношениях между сторонами и углами треугольника, признака равнобед-ренного треугольника, теоремы о неравенстве треуголь-ника. Уметь: - сравнивать углы, стороны треугольника, опираясь на соотношения между сторонами и углами треугольника;- решать задачи, используя признак равно-бедренного треугольника и теорему о неравенстве треугольника. | Фронтальный и индиви-дуальный опрос, самостоятельная работа |
|
|
|
| 29 | Решение задач на нахождение площади треугольника | Применение знаний и умений | Знать различные формулы для нахождения площади треугольника. Уметь находить площадь треугольника различными способами. | Фронтальный и инди-видуальный опрос |
|
|
|
| 30 | Решение задач на нахождение площадей прямоугольника и квадрата | Применение знаний и умений | Знать формулы площадей прямоугольника и квадрата. Уметь находить площади прямоугольника и квадрата, используя соответствующие формулы. | Фронтальный и инди-видуальный опрос |
|
|
|
| 31 | Решение задач на нахождение площадей параллелограмма и ромба | Применение знаний и умений | Знать формулы для вычисления площадей параллелограмма и ромба. Уметь находить площади параллелограмма и ромба, используя формулы. | Фронтальный и инди-видуальный опрос |
|
|
|
| 32 | Решение задач на нахождение площади трапеции | Применение знаний и умений | Знать формулировку теоремы о площади трапеции. Уметь находить площадь трапеции, используя формулу. | Фронтальный и инди-видуальный опрос |
|
|
|
| 33 | Решение задач на нахождение площади круга и площади сектора | Применение знаний и умений | Знать формулы площади круга и кругового сектора. Уметь находить площадь круга и кругового сектора. | Фронтальный и инди-видуальный опрос |
|
|
|
| 34 | Нахождение площадей треугольника, четырёхугольников, круга и сектора | Комбинированный | Знать и уметь применять формулы при решении задач. | Фронтальный и индиви-дуальный опрос, самостоятельная работа |
|
|
|
| 35 | Итоговое занятие | Комбинированный | Уметь: решать основные задачи. | Фронтальный и инди-видуальный опрос |
|
|
|
Требования к уровню подготовки установлены Государственным стандартом основного общего образования в соответствии с обязательным минимумом содержания. В результате изучения курса учащиеся должны: знать/понимать: – значение математической науки для решения задач, возникающих в теории и практике; – существо понятия алгоритма; – значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа, возникновения и развития геометрии. – как используются математические формулы и уравнения при решении математических и практических задач; – смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации. уметь: – выполнять арифметические действия, сочетая устные и письменные приёмы, применяя вычислительные устройства; – представлять проценты в виде дроби и дробь в виде процентов; – решать текстовые задачи арифметическим способом и с помощью уравнений, включая задачи, связанные с процентами; – проводить по известным формулам и правилам преобразования буквенных выражений, включающих тригонометрические функции; – вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; – выражать из формул одну переменную через другую; – решать линейные уравнения, системы двух линейных уравнений; – описывать свойства изученных функций, строить их графики; – находить по графику наибольшие и наименьшие значения; – пользоваться геометрическим языком для описания предметов окружающего мира; – распознавать, изображать геометрические фигуры; выполнять чертежи по условию задач; – проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая, возможности для их использования; – решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей); использовать приобретённые знания и умения в практической деятельности и повседневной жизни: – для решения несложных практических задач, в том числе с использованием справочных материалов, калькулятора, компьютера; – устной прикидки и оценки результатов вычислений; проверки результатов вычислений с использованием различных приёмов; – интерпретации результатов решения задач с учётом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений; – для расчётов по формулам, включая формулы содержащие тригонометрические функции, обращаясь при необходимости к справочным материалам и применяя простейшие вычислительные устройства; – для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков; – для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур; – для описания реальных ситуаций на языке геометрии; – для вычисления площадей фигур при решении практических задач, используя при необходимости справочники и вычислительные устройства. – для решения практических задач, связанных с нахождением геометрических величин; – для построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Квадратные уравнения. Формула корней квадратного уравнения. Теорема Виета.
Понятие площади многоугольника. Площади прямоугольника, ромба, квадрата, параллелограмма, трапеции, треугольника. Площадь круга, площадь кругового сектора..
Программа является авторской, разработана на основе: - «Программы общеобразовательных учреждений. Алгебра 10-11 классы. Составитель Т. А. Бурмистрова. – М.: Просвещение, 2009 г.»; - «Программы общеоб-разовательных учреждений. Геометрия 10-11 классы. Составитель Т. А. Бурмистрова. – М.: Просвещение, 2010 г.»; : - Программы общеобразовательных учреждений. Алгебра 7-9 классы. Составитель Т. А. Бурмист-рова – М.: Просвещение, 2009 г.; - Программы общеобразовательных учреждений. Геометрия 7-9 классы. Составитель Т. А. Бурмистрова – М.: Просвещение, 2009 г. Данный предмет предлагает учащимся знакомство с математикой как с общекультурной ценностью, выработкой понимания ими того, что математика является инструментом познания окружающего мира и самого себя. Данный предмет отражает обязательную для всех школьников инвариативную часть образования. Предлагаемый предмет является развитием системы ранее приобретенных программных знаний, предусматривает повторное рассмотрение теоретического материала по математике, а кроме этого, нацелен на более глубокое рассмотрение отдельных тем, поэтому имеет большое общеобразовательное значение, способствует развитию логического мышления; его цель - создать целостное представление о теме и значительно расширить спектр задач, посильных для учащихся. Программа рассчитана на 35 ч. Она предназначена для повышения эффективности подготовки учащихся к итоговой аттестации по математике за курс полной средней школы, посвящена ключевым темам курса математики 7-9 классов. Изучение данного предмета направлено на достижение следующих целей: - интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, способности к преодолению трудностей; - формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов; - совершенствование математической культуры и творческих способностей учащихся на основе коррекции базовых математических знаний учащихся; - систематизация математических знаний и умений, необходимых в практической деятельности и продолжения образования. Задачи для достижения поставленных целей: - формирование у учащихся устойчивого интереса к предмету;
- подготовка к государственной итоговой аттестации в форме ЕГЭ. Каждое занятие состоит из двух частей: задачи, решаемые с учителем, задания для самостоятельного или домашнего решения, тестирование, заполнение бланков ответов.
Особенности курса занятий по данному предмету: - краткость изучения материала математики 7-9 классов; - практическая значимость для учащихся.
















