| Тема урока: переместительное и сочетательное свойство умножения рациональных чисел | Школа: ОСШ.№16 им.Ш.Уалиханова |
|
| Дата:29.11.2016 | ФИО учителя. Тойчиева З.А |
|
| КЛАСС: 6 а.б | Количество присутствующих: | Количество отсутствующих: |
|
| Цели обучения, которые необходимо достичь на данном уроке | Способствовать развитию умения применять переместительный и сочетательный законы умножения к рациональным числам, используя прошлый опыт (натуральные, целые числа и десятичные дроби); Развитие интереса учащихся к предмету; математического и общего кругозора, мышления и речи, внимания и памяти; воспитание ответственности, аккуратности, самостоятельности. |
|
| Цели обучения | Все учащиеся смогут: |
|
| |
|
| Большинство учащихся будут уметь: |
|
| Умножать рациональные числа. умеют применять полученные знания на практике. |
|
| Некоторые учащиеся смогут: |
|
| Знают правило умножения рациональных чисел
|
|
| Языковая цель | Учащиеся могут: умеют анализировать и использовать информацию при актуализации знаний и при изучении новой темы. - работают коллективно, в парах. |
|
| Ключевые слова и фразы: |
|
| Умножение |
|
| Стиль языка, подходящий для диалога/письма в классе:
Discuss the chart that is created. Which is the most popular fruit choice? How do we know? Has every learner’s choice been recorded? How can we check? Ask learners if they can think of other questions that we might have investigated. If ideas are not forthcoming, ‘lead’ the discussion by suggesting – what else could we have put in the basket? What other things could we try, to see if people have favourites? What other questions could we have asked about our fruit basket? Take ideas and ask – What do you think the result might be? What would the pictogram look like?
|
|
| Вопросы для обсуждения: |
|
- Если перемножить четыре отрицательных числа, каков будет результат? - Если перемножить семь отрицательных чисел, каков будет результат? - Сформулируйте правило для умножения отрицательных чисел с помощью понятий «чётный» и «нечётный». - Запишите основные правила с помощью правило знаков при умножения
|
|
| Можете ли вы сказать, почему...? |
|
|
|
|
| Подсказки: |
|
| Правило знаков |
|
| Предыдущее обучение | Умножение рациональных чисел |
|
| План Организационный момент. 2. Погружение в проблемную ситуацию. Формулировка темы урока. Постановка цели урока.
3. Актуализация знаний.
4. Открытие новых знаний
5. Закрепление нового материала. Дифференцированная самостоятельная работа. 6. Рефлексия. Итог и домашнее задание(дифференцированное).
|
|
| Планируемые сроки | Модули | Планируемые действия (замените записи ниже запланированными действиями)
| Деятельность ученика | Ресурсы |
|
| Начало урока
|
Критическое мышление
Диалог | Орг.момент(10 мин) Психологический настрой на урок.
) – 8,4 + (– 8,4) = 0; (– 16,8) 2) (– 6,7) . (– 10) = – 67; (67) 3) (– 2,2) + 3,5 = 1,3; 4) – 13 – 8 = – 5; (– 21) 5) 15 – 18 = – 13; (– 3) 6) 7,4 – (– 3,2) = – 10,6; (10,6) 7) – 9 . 6 = – 54; 8) – 3,6 . 1 = –1; (– 3,6) 10) – 3,7 . 0 = – 3,7. (0) | Ученики демонстрируют свои знания | карточки |
|
| Середина урока | Управление и лидерство | Работа в группе;(15 мин) Изучение новой темы: А теперь давайте рассмотрим свойства умножения. Свойства умножения неотрицательных чисел также справедливы и для любых рациональных чисел. Умножение, как и сложение, обладает переместительным и сочетательным свойствами. 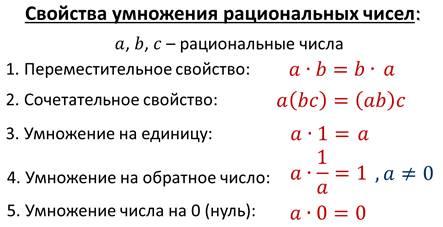 Переместительное и сочетательное свойства умножения позволяют переставлять и группировать множители, что дает возможность упрощать выражения. Задание Найдите произведение. 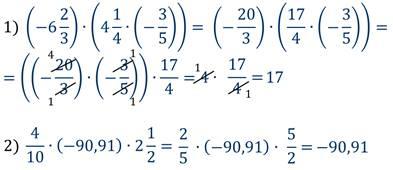 Умножение рациональных чисел обладает и распределительным свойством умножения относительно сложения. Для любых рациональных чисел а, b и с верно равенство: 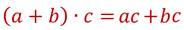 Для того чтобы умножить сумму на число можно сначала умножить первое слагаемое на это число, потом второе слагаемое на это число, а затем полученные результаты сложить. Пример 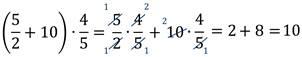 Распределительное свойство умножения справедливо и в обратную сторону.  Такое преобразование выражения называют вынесением общего множителя за скобки. Пример 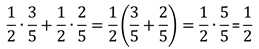 Решение в задачи в группах. Расположить результаты в порядке возрастания и расшифруй названия геометрических фигур: -0,5 · 40 Р -20 -0,1 · (-3) О 0,3 0,9 · (-0,6) С -0,566 -0,04 · (-10) К 0,4 -1 · 3,2 Д -3,2 3,6 · 2 И 7,2 -10 · 0,1 А -1 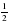 · (-4) Э -2 · (-4) Э -2 | Учащиеся самостоятельно изучают тему.
Учащиеся записывают все, что узнали по данной теме. Оценивают работу своих одноклассников. На стикерах записывают свое мнение по поводу урока. |
Учебник |
|
| Конец урока | оценивание |
Закрепление групп. (10 мин) 1 группа Найдите произведение -8·(-6). Вычислите: 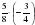 . . Найдите значение выражения х3 при х = - 4. Решите уравнение х: (-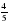 )= - 1,5 )= - 1,5 2 группа Найдите произведение -7·9 . Вычислите: -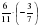 Найдите значение выражения х3 при х = -5. Решите уравнение: х: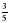 =-2,5 =-2,5
Итог урока. Этап рефлексии: - О чем говорили на уроке? - Что удалось без особых усилий? - Что было трудно? Домашняя работа:
| Учащиеся оценивают свою деятельность на уроке, выставляют себе оценку и записывают домашнее задание.
| стикеры |
|
| Дополнительная информация |
|
| Дифференциация. Как вы планируете поддерживать учащихся? Как вы планируете стимулировать способных учащихся? | Оценивание. Как вы планируете увидеть приобретенные знания учащихся? | Межпредметные связи
соблюдение СанПиН ИКТ компетентность
Связи с ценностями |
|
| | | |
|
| Рефлексия Были ли цели обучения реалистичными? Что учащиеся сегодня изучили? На что была направлено обучение? Хорошо ли сработала запланированная дифференциация? Выдерживалось ли время обучения? Какие изменения из данного плана я реализовал и почему?
| Используйте пространство ниже, чтобы подвести итоги урока. Ответьте на самые актуальные вопросы об уроке из блока слева. |
|
|
|
|
| Итоговая оценка
Какие два аспекта в обучении прошли очень хорошо (с учетом преподавания и учения)?
1:
2:
Какие два обстоятельства могли бы улучшить урок (с учетом преподавания и учения)?
1:
2:
Что узнал об учениках в целом или отдельных лицах?
|

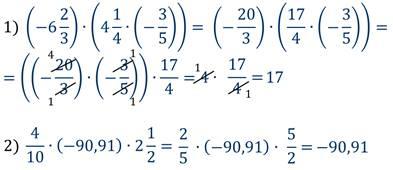
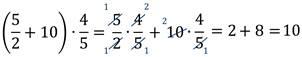
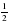 · (-4) Э -2
· (-4) Э -2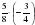 .
.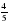 )= - 1,5
)= - 1,5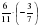
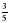 =-2,5
=-2,5















