Интеллектуальная игра
«Математическая абака»
для учащихся 5 класса.
Скубачева Марина Николаевна
учитель математики
МБОУ «СОШ № 9»
п. Октябрьский
Тбилисский район
2015 г.
Интеллектуальная игра
«Математическая абака»
для учащихся 5 класса.
Цели:
образовательные:
воспитательные:
воспитание у учащихся инициативности, смекалки;
развитие доброжелательного отношения друг к другу;
развитие умения управлять своим поведением, следовать требованиям коллектива;
развивающие:
нацелить на сотрудничество и творчество;
повысить познавательный интерес к математике;
научить умению логически мыслить, анализировать и обобщать;
Формируемые УУД:
регулятивные – умение организовать себя, настраиваться на работу, применять теоретические и практические знаний по предмету, выделять в условии задачи данные необходимые для решения задачи, строить логическую цепочку рассуждений;
познавательные – умение ориентироваться, понимать информацию представленную в виде текста; владеть общим приемом решения учебных задач, создавать и преобразовывать модели и схемы для решения задач, осуществлять выбор наиболее эффективных способов решения образовательных задач в зависимости от конкретных условий, осуществлять сравнение, классификацию по заданным критериям, строить рассуждения в форме связи простых суждений об объекте, его строении, свойствах и связях;
коммуникативные – умение вступать в диалог, участвовать в коллективном обсуждении учебной проблемы, оформлять свои мысли в устной и письменной форме, устанавливать и сравнивать разные точки зрения, прежде чем принимать решение и делать выбор.
Оборудование: мультимедийный проектор, компьютер, презентация, листы бумаги, ручка.
Правила
Математическая абака — это командная игра-соревнование по решению задач. Все задачи выдаются для решения всем командам одновременно. Основным зачётным показателем в математической абаке является общее количество набранных очков (включая бонусы). В случае равенства очков у нескольких команд более высокое место занимает команда, имеющая большую сумму бонусов. При равенстве и этого показателя команды считаются разделившими места.
Решение задач
Игроки разделяются на команды по 4-6 человек. Каждая команда сразу получает условия всех задач. Задачи разделяются по 6 темам, в каждой теме находится по одной задаче каждого из 6 уровней сложности
Задачи каждой темы сдаются по порядку, от 1-й до 6-й (например, у команды не примут ответ на задачу №4, пока она не сдала ответы на задачи №1, №2 и №3 по этой же теме). На каждую задачу дается одна попытка сдать ответ. Если команда предъявляет правильный ответ на задачу, она получает за это цену задачи, а если ответ неправильный или неполный, команда получает 0 очков.
Цена первой задачи каждой темы - 10 очков, второй - 20, третий-30, четвертый – 40, пятый - 50, шестой - 60 очков. Таким образом, не считая бонусов, команда может заработать за решение задач до 6·210 = 1260 очков.
Бонусы
Каждая команда дополнительно может заработать бонусы:
Бонус-горизонталь (за правильное решение всех задач одной темы) — 50 очков.
Бонус-вертикаль (за правильное решение задач с одним и тем же номером по всем темам) — цена задачи с этим номером.
Бонусы за первое решение: первая команда, получившая одну из шести возможных бонус-горизонталей или одну из шести бонус-вертикалей, получает соответствующий бонус в двойном размере.
Окончание игры
На решение задач отводится 40 минут. Команда заканчивает игру, если у нее кончились задачи или истекло общее время, отведенное для игры.
Ход игры.
I. Организационный момент
II. Актуализация. Вступительное слово учителя.
На сегодняшней “Математической абаке” вы посоревнуетесь в умении решать задачи, применяя смекалку и сообразительность. Как сказал Паскаль: “Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным”.
Быстрее и точнее – вот единственное требование в этой незамысловатой игре.
IV. Представление команд.
V. Игра команд.
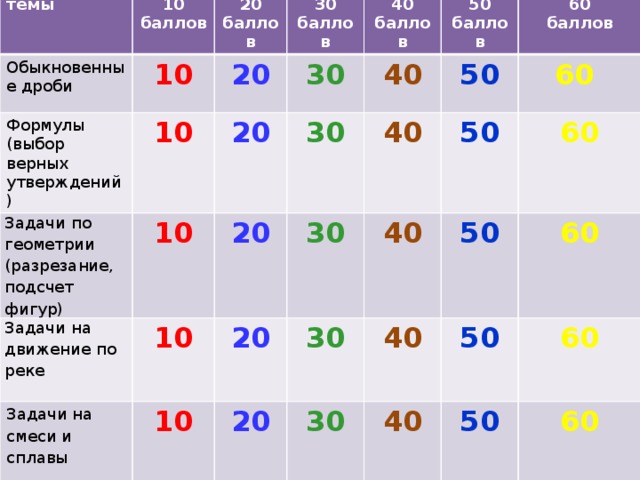
|
| 10 | 20 | 30 | 40 | 50 | 60 |
| Обыкновенные дроби | Какую долю составляют сутки от года? | В книге 328 страниц. Абат прочитал из них 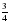 . Сколько страниц еще осталось прочитать? . Сколько страниц еще осталось прочитать? | Длина минутной стрелки Кремлевских курантов – 328 см. Высота цифр на циферблате составляет 9/41 от длины минутной стрелки. Вычисли высоту цифр на циферблате Кремлевских курантов. | Из 128 изделий прикладного искусства, выставленных на выставке, 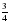 составляют изделия из глины, остальные – изделия из дерева. Сколько изделий из дерева было на выставке? составляют изделия из глины, остальные – изделия из дерева. Сколько изделий из дерева было на выставке? | В магазин завезли 320 компьютеров. Для учреждений купили 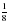 компьютеров, а для школ - компьютеров, а для школ - 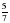 оставшегося количества. Сколько компьютеров купили для школ? оставшегося количества. Сколько компьютеров купили для школ? | Оборона занимает прямоугольный участок местности. Линия обороны имеет длину 90 км. Одна из наибольшей стороны прямоугольника является передним краем и равна 3/9 линии обороны, а ширина – 3/6 большей стороны. Определить площадь участка обороны. |
| Формулы (выбор верных утверждений) | Выберите неверное утверждение.
А) Если в конце десятичной дроби приписать нуль, то получится дробь, равная данной;
Б) если после разряда округления стоит цифра 5, то при округлении разряд округления не меняется;
В) приближённое значение с недостатком меньше приближённого значения с избытком;
Г) при вычитании десятичных дробей дроби записывают таким образом, чтобы запятая находилась под запятой. | Выберите верное утверждение.
А) Любую дробь со знаменателем 10 можно записать в виде десятичной дроби;
Б) равные десятичные дроби изображаются на координатном луче разными точками;
В) десятичные дроби нельзя сравнивать по разрядам;
Г) при сложении десятичных дробей в сумме отделяется столько цифр, сколько их стоит в обоих слагаемых вместе.
| Выберите верное неравенство.
А) 27,2 Б) 1680 1860; В) 11,68 1,68; Г) 19,99 | Если сторону квадрата увеличить на на 4 единицы, то его периметр… 1. увеличится на 4 единицы. 2. увеличится на 16 единиц. 3. увеличится. 4. увеличится, но не на 16 единиц. 5. увеличится на 8 единиц.
| Если автомобиль по грунтовой дороге пройдет в первую минуту 300 м, во вторую – 500 м, 11 минут по 800 м, одну минуту – 400 м и одну минуту – 200 метров, то средняя скорость автомобиля на этом участке пути может быть… 1. 680 м /мин. 2. более 40 км /ч. 3. (300+500+800х11+400+200): 15м/мин. | Мальчики заговорили о Сережиных марках. У него их не меньше 1000, - сказал Петя.
-Ты не прав,у него из меньше, - возразил Андрей. Но одна-то у него наверняка есть, - добавил Антон.
Известно,что из этих трёх утверждений только одно верное. Сколько марок у Сергея?
|
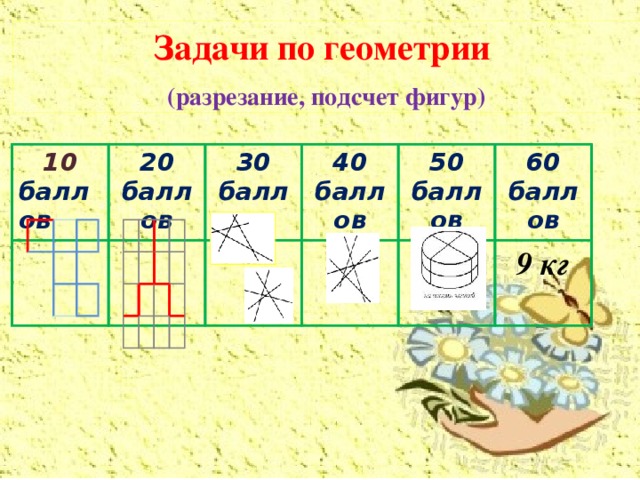
| Задачи по геометрии (разрезание, подсчет фигур) | На рисунке изображены пять квадратов, составленных из шестнадцати спичек. Переставьте три спички так, чтобы получилось четыре одинаковых квадрата | Разделите фигуру на три равные части так, чтобы линия разреза шла по сторонам квадратов
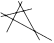
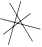
| Проведите через шесть точек четыре прямые так, чтобы на каждой прямой было по три точки.
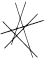
| Проведите через 10 точек пять прямых так, чтобы на каждой было по четыре точки.
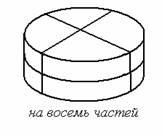
| Как тремя прямолинейными разрезами разделить круглый торт на:
восемь частей?
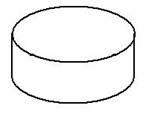
| Для того, чтобы покрасить кубик, изображенный на левом рисунке (Рисунок 14), понадобится 9 кг краски. Сколько краски потребуется, чтобы покрасить фигуру, изображенную на правом рисунке?
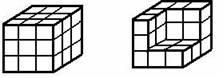
|
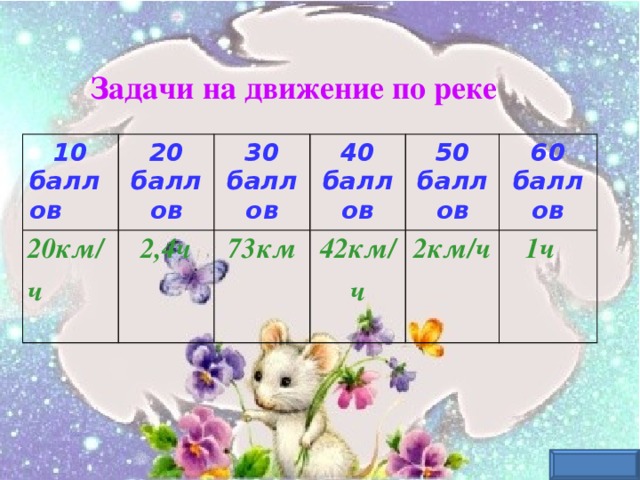
| Задачи на движение по реке
| Катер за 3 часа проплыл по озеру 60 км. Найдите собственную скорость катера. | Собственная скорость катера34 км/ч, скорость течения реки 2,5 км/ч. Сколько времени затратит катер на путь по течению реки между двумя селами, если расстояние между ними 87,6 км?
| Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению реки и 3часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
| Скорость катера по течению реки 44 км/ч, а против течения 40 км/ч. Какова скорость катера в стоячей воде. | За 9 часов лодка проходит такое же расстояние по течению, что за 18 часов против. Найти скорость течения, если скорость лодки 6 км/ч | Моторная лодка проплывает некоторое расстояние по озеру за 40 мин, а такое же расстояние против течения реки она проплывает за 60 мин. За сколько минут моторная лодка проплывает такое же расстояние по течению реки? |
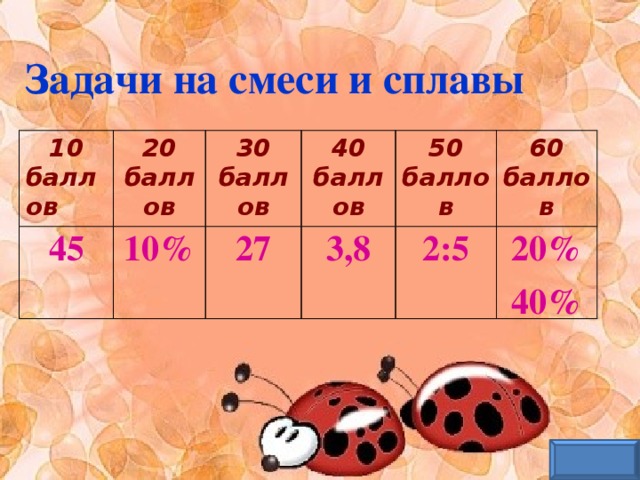
| Задачи на смеси и сплавы
| 9% от 500. | Килограмм соли растворили в 9 л воды. Какова концентрация раствора?
| Смешали 250 г, 300 г и 450 г азотной кислоты соответственно 20%, 30% и 40% концентрации. Какова концентрация смеси? | В 5% раствор кислоты массой 3,8 кг добавили 1,2 кг чистой воды. Чему стала равна концентрация раствора (в процентах)? | Смешивая 5% и 40% растворы кислот, необходимо получить 30% раствор. В каком соотношении их необходимо взять?
| Из двух сплавов, один из которых содержит 20% олово, а другой - 40% олова, необходимо получить сплав массой 4 кг, который содержал бы 25 % олова. Сколько килограммов каждого сплава необходимо для этого взять? |
|
Модуль числа
| Вычислите | (|4,75:0,5 -8,007)| |
Сравните 56-| -14+8| и|56-14|+8 |
Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5. |
Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5. |
Решите уравнение
6-|x|=2. |
Поставьте знаки модуля так, чтобы равенство 1-2-4-8-16=19 стало верным.
|
Ответы:
|
| 10 | 20 | 30 | 40 | 50 | 60 | Бонусы | Бонус за первое решение | Общая сумма
|
| Обыкновенные дроби | 1/365 или 1/366 | 82 страницы | 150: 5/7 = 210 (км)
| 32 | 200
| 450 км2
|
|
|
|
| Формулы (выбор верных утверждений) | Б | А | В | 2 | 3 | у Сережи было больше 1000 марок.
|
|
|
|
| Задачи по геометрии (разрезание, подсчет фигур) | 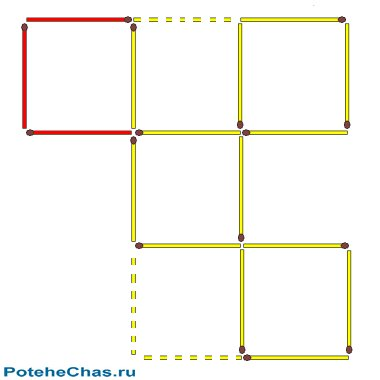
|
|  
|
|
| 9 кг |
|
|
|
| Задачи на движение по реке
| 20км/ч | 2,4ч | 73км | 42км/ч | 2км/ч | 1ч |
|
|
|
| Задачи на смеси и сплавы
| 45
| 10% | 27 | 3,8 | 2:5 | 20% и 40% |
|
|
|
| Модуль числа
| 1,493 | ˃ | -4;-3;-2; -1;0;1;2;3;4 | 1;2;3;4 | -4;+4 | 1) |1-2|-|4-8|-16=19
2) |1-2-|4-8|-16|=19
3) ||1-2|-|4-8|-16|=19
4) ||1-2|-4-8-16|=19 |
|
|
|
Презентация к игре.
VI. Подведение итогов игры:
- Наша игра подошла к концу. Всем большое спасибо за участие! Хочу закончить наше мероприятие словами:
Порой задача не решается,
Но это, в общем, не беда,
Ведь солнце все же улыбается,
Не унывая никогда.
Друзья всегда тебе помогут,
Поверь в себя –
И ты все сможешь,
Иди вперед – и победишь!
Литература
Математика. Предметные недели в школе. С.В.Виноградова, Н.Н.Деменева Волгоград «Учитель» 2007 г.
Задачи мудрецов. Л.М.Лихтарников Москва. Просвещение 1996 г.
Математические олимпиады в школе 5-11 классы А.В.Фарков
Учимся решать олимпиадные задачи. Геометрия. А.В.Фарков М. Айрис-пресс 2006 г.
Проверочные задания по математике. Л.М.Буланова Москва. Просвещение 1991 г.
Задачи по математике для 4-5 классов И.В.Баранова Москва. Просвещение 1988 г.
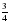 . Сколько страниц еще осталось прочитать?
. Сколько страниц еще осталось прочитать?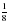 компьютеров, а для школ -
компьютеров, а для школ - 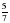 оставшегося количества. Сколько компьютеров купили для школ?
оставшегося количества. Сколько компьютеров купили для школ?