Исследовательская работа по математике "Флексоры и флексагоны"

^{XXV Ставропольская краевая открытая научная конференция школьников}

^{Секция: юниор (математика)}

^{Название работы: «Чудеса геометрии. Флегсагоны и Флексоры»}

^{Автор работы: Казаков Семен Михайлович}

Место выполнения работы: ст.Григорополисская

МОУ СОШ №2, 4 класс.

Научный руководитель :

Кузнецова Елена Ивановна

учитель математики МОУ СОШ № 2

^{Ставрополь, 2014}

Оглавление

Введение…………………………………………… ………… 3

Постановка проблемы ...… ………… …5

Построение и исследование флексагонов ……… ….. 6

Построение и исследование флексоров ……… ….… 11

Анкетирование ----------------------------------------------------------15

Применение флексагонов и флексоров ………… ….. 16

Заключение …………………………………………………… 17

Библиографический список………………………………….. 18

Приложения-----------------------------------------------------------------19

Введение

"Геометрия является самым могущественным

средством для изощрения наших умственных

способностей и дает нам возможность

правильно мыслить и рассуждать"

Галилео Галилей

Все мы любим занимательную математику. Занимательная математика пробуждает наблюдательность, умение логически мыслить, веру в свои силы. Элемент игры, который делает занимательную математику интересной, может иметь форму головоломки, состязания, фокуса, парадокса и т.д.

Не так уж велико различие между восторгом человека, сумевшего найти ключ к сложной головоломке, и радостью математика, преодолевшего еще одно препятствие на пути к решению сложной научной проблемы. И тот и другой заняты поисками истиной красоты – того ясного, четко определенного, загадочного и восхитительного порядка, что лежит в основе всех явлений. Неудивительно поэтому, что чистую математику порой трудно отличить от занимательной и мой проект «Флексагоны и флексоры» это подтверждает.

Интерес к головоломкам подтолкнул меня к более серьезному изучению и анализу, простых казалось бы вещей. Появилось желание не только повторить уже известные факты, но и додумать что-то самому. Стали понятны слова Д. Пойа: «Лучший способ изучить что-либо - это открыть самому». Так появилась желание изучить мир флексагонов и флексоров.

Проектный продукт: схемы сборки некоторых флексагонов, флексагоны, флексоры, рекомендации по изготовлению флексагонов.

Цель исследовательской работы: показать, что в основе таких геометрических игрушек, как флексагоны и флексоры, лежит математика.

Задачи: составление анкеты, выявляющей интерес учащихся к занимательной геометрии; изучение и анализ информации о флексагонах и флексорах; нахождение практического применения флексагонам и флексорам; изготовление брошюры «Геометрические игрушки: практическое пособие по изготовлению флексагонов и флексоров».

Методы исследования: изучение специальной литературы; изготовление и практическое применение флексагонов и флексоров; анкетирование и анализ анкет; фотографирование процесса.

Гипотеза: флексагоны способствуют развитию творчества, логического мышления.

.

Объектом исследования является математика.

Предмет исследования – геометрия гнущихся многогранников.

Актуальность выбранной темы:
На первый взгляд, флексагоны и им подобные фигуры (обладающие удивительной способностью изгибаться, показывая новые грани) ‒ всего лишь игрушки. Но они сумели привлечь внимание в различных отраслях. Вот несколько тому доказательств:

• 
  Шарнир двойного действия, соединение которого присутствует на всех тетрафлексагонах, повсеместно используется для петель дверей и окон, в креплениях на настенные телевизоры, в раскладных телефонах.

• 
  Флексагоны связаны со многими математическими понятиями: лентой Мёбиуса, Тором (тороидом). Помимо этого эти «игрушки» подчинены строгим правилам математики, которые изучает наука флексология. 

• 
  Необычный цикл изгибания фигур привлекает к ним внимание, из-за этого его используют в рекламных акциях (канал сайта http://rutube.ru/tracks/4188813.html). Помимо этого к любому флексагону можно прикрепить плоский предмет (то, на что изготовители хотят обратить внимание), и можно быть уверенным, что этим предметом заинтересуются (также используется в маркетинге).

• 
  Флексагоны связаны с различными науками и вещами: в форме флексагонов закручены молекулы веществ (журнал «Химия и жизнь»), в стиле флексагонов создаются интерьеры помещений и предметы меблировки (страница сайта http://www.osvetleni-daylight.cz/designova-stolni-lampa-flexagon-white-p-1466.html?zenid=f80a554ef57c674b587d29e31e443d52).

• 
  Наконец, флексагоноподобные фигуры используются как самодельные открытки, игрушки (к сожалению, массовое производство так и не налажено). Они служат темами как научных, так и ненаучных дискуссий, но до конца их тайны ещё не раскрыты.

Благодаря самостоятельному изготовлению моделей флексагонов и флексоров, проведенных над ними исследований, удалось лучше понять и изучить их мир, т.е. добиться поставленной цели.

Конечно, на это ушло достаточно времени (5-6 месяцев). Если выбор и название темы не вызвали затруднений, то поиск информации (интернет, библиотека), построение чертежей, разработка схем сборки, сама сборка моделей и исследования, проведенные над ними, а также конкретизация и оформление материала потребовали много усилий и времени.

Постановка проблемы

Всё начиналось очень просто. Блуждая по страницам интернета, я обнаружил видео мальчика, который, изгибая бумажку, выворачивал всё новые и новые картинки. Обожая головоломки, я тоже захотел такую игрушку. С этого момента всё и началось, но тогда я ещё не знал, что буду работать над проектом. Стал искать информацию. Оказалось, это игрушка – флексагон (англ. toflex - складываться, сгибаться, гнуться). Как построить? Где взять чертеж? Помог М. Гарднер! Именно из его книгия узнал и историю возникновения флексагонов, и как их построить, позаимствовал чертежи для дальнейшей работы над флексагонами.

Так что же это такое?!

Флексагоны - это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной, изогнутой формы, которые обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а раннее скрываемые поверхности неожиданно выходят наружу¹.

Интересный факт: придумать флексагоны помогло одно случайное обстоятельство - различие в формате английских и американских блокнотов. Флексагоны,не были бы открыты и по сей день, и многие выдающиеся математики лишились бы удовольствия изучать их замысловатую структуру. Если бы в конце 1939 года, Артур Х. Стоун, двадцатитрехлетний аспирант из Англии, изучавший математику в Пристоне, обрезая листы американского блокнота, не пожелал немного развлечься. Стоун принялся складывать из отрезанных полосок бумаги различные фигуры. Одна из сделанных им фигур оказалась особенно интересной. Перегнув полоску бумаги в трёх местах и соединив концы, он получил правильный шестиугольник (рис.1).Взяв, этот шестиугольник, за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Если бы обе стороны исходного шестиугольника были разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Был открыт самый первый флексагон! Он был назван тригексафлексагоном, так как у него три поверхности, (гексаот греческого «гекс», что означает шесть), флексагонами - из-за их способности складываться. Вторая не менее изящная модель получила название гексагексафлексагона (первое «гекса» - шесть - означает число поверхностей этой модели). Друзьями был создан «Флексагонный комитет», который обнаружилчто, удлиняя цепочку треугольников, можно делать флексагоны с 9, 12, 15 и даже большим числом поверхностей.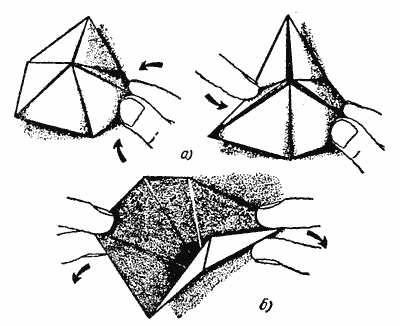

рис. 1

По предлагающимся выкройкам, с помощью подробного описания, я быстро изготовил флексагоны с тремя и шестью поверхностями. Наигравшись первым и не поняв все тайны второго, я захотел изготовить флексагоны с четырьмя и пятью поверхностями (тем более что выкройки прилагались). И тут возникла первая проблема: выкройки есть, а описания их складывания - нет! Опять обратился к поиску литературы: интернет-ресурсы, журналы «Квант», работы других участников фестиваля «Портфолио» … И везде один результат - только чертежи, без подробных инструкций. Обратился за помощью к учителю, а она предложила мне самому разработать инструкции для интересующих меня моделей. Так началась работа над практико-ориентированным проектом «Флексагоны и флексоры» (флексоры были добавлены в ходе работы).

Построение и исследования флексагонов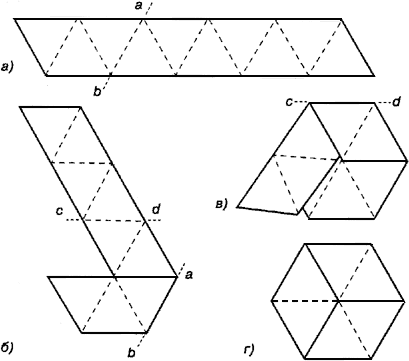

Приступая к разработке схем для сборки тетрагексафлексагона и пентагексафлексагона и имея опыт по сборке тригексафлексагона и гексагексафлексагона, я уже понимал, что: 1) нужно найти такой способ расстановки чисел на имеющихся чертежах, чтобы он привел меня к полоске из десяти треугольников (рис.2), схема сборки которой имеется в научной литературе.

2) Если каждый треугольник пометить числом или символом,то чередование символов на развернутой полоске будет обладать определенной периодичностью. Например, на лицевой и обратной сторонах развертки гексагексафлексагона, цифры будут располагаться в такой последовательности: 123123 123123 123123 (лицевая),

445566 445566 445566 (обратная).

Теперь, методом проб и ошибок, мне предстояло определить порядок расстановки чисел в имеющихся чертежах, так, чтобы флексагоны «заработали». Результатом моих трудов явились следующие схемы сборки:

1. Тетрагексафлексагон:

3

3

3

1

1

1

3

3

3

2

2

2

4

4

4

1

1

1

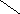
4

4

4

2

2

2

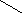
2. Пентагексафлексагон:

5

5

5

2

2

2

1

1

1

5

5

5

4

4

4

3

3

3

1

1

1

4

4

4

2

2

2

3

3

3

Построив флексагоны с 3-мя и 6-ю поверхностями (по Гарнеру), с 4-мя и 5-ю поверхностями по своим разработкам, понял, что хочется чего-то более сложного, так появились разработки для гексагексафлексагона (второго вида), гептагексафлексагона и додекагексафлексагона:

3. Гексагексафлексагон (второго типа):

2

6

5

4

3

2

1

1

4

6

5

3

4

6

6

5

4

3

2

1

3

6

5

5

4

3

2

1

6

5

4

3

2

2

1

1

4. Гептагексафлексагон:

1

1

3

3

3

2

2

2

2

1

1

7

7

6

4

4

6

6

6

5

5

7

7

3

1

3

3

2

2

1

7

5

4

4

4

4

6

6

6

5

5

5

7

5. Додекагексафлексагон (37 правильных треугольников):

6

6

6

6

5

5

5

5

5

4

4

4

4

4

3

3

3

3

3

2

2

2

2

2

1

1

1

1

1

7

8

9

11

10

8

11

7

8

10

9

7

12

12

7

8

12

11

9

11

10

9

8

10

8

12

7

7

В ходе работы были сделаны первые выводы:

Сборку флексагона нужно начинать с наибольшего числа и складывать так, чтобы треугольники, имеющие одинаковые числа, оказались наложенными друг на друга. Например, для изготовления гептагексафлексагона сначала собирают все 7 на 7, затем 6 на 6, 5 на 5, 4 на 4, после чего получаем полоску из 10 треугольников. При сборке любой модели всегда приходим к полоске из 10 треугольников!

Имея перед собой готовые модели шестиугольников, хотелось увидеть, как они работают. Если в моделях с 3-мя, 4-мя, 5-ю поверхностями отыскать каждую поверхность не составило большого труда, то начиная с гексагексафлексагона, появились трудности. Флексагон можно было вращать до бесконечности, но увидеть пятую, шестую и т.д. поверхности так и не удавалось! И снова на помощь пришли статьи из журналов.Разобраться помогла схема разработанная Таккерманом для гексагексафлексагона. Им был найден простейший способ выявления всех поверхностей любого флексагона: держа флексагон за какой-нибудь угол, следует открывать фигуру до тех пор, пока она «открывается», а затем переходить к следующему углу. Этот метод так и называется «путь Таккермана». Он позволяет увидеть все шесть разворотов гексагексафлексагона за один цикл из 12 сгибаний. Стрелки указывают, в каком порядке становятся видимыми поверхности флексагона. Если модель перевернуть, то путь Таккермана будет изображаться той же схемой, но направление её обхода будет противоположным.

И после нахождения всех поверхностей, работу над флексагонами нельзя было назвать законченной. Впереди предстоял большой творческий процесс. Чтобы вращение флексагона доставило ещё больше эмоций и удовольствия, каждую поверхность флексагона нужно было раскрасить. И для этого тоже существует правило! Существует множество способов раскраски флексагонов, которые приводят к интересным головоломкам и самым неожиданным зрительным эффектам. Так, каждая поверхность флексагона может появляться, по крайней мере, в двух различных видах в зависимости от того, как повернуты относительно друг друга образующие её треугольники. Например, если каждую поверхность разделить на части так, как показано на рисунке 4, и выкрасить области А, В и С в различные цвета, то в центре видимой поверхности могут появиться и области А, и области В, и области С.

Геометрический узор, который нарисован на одном развороте флексагона, появляется на двух других разворотах, каждый раз принимая иной вид.

рис.4

Работу, проделанную над флексагонами, нужно было систематизировать. Для этой цели, свою коллекцию флексагонов я дополнил уна - и дуогексафлексагонами (их сделать было несложно, описание есть в научной литературе). Исследовал и сфотографировалкаждую поверхность (первые шестьфлексагонов см. Проектный продукт).

Получены следующие результаты:

а) унагексафлексагон - этот простейший экземпляр представляет собой лист Мёбиуса² с треугольным краем. Он имеет одну поверхность и состоит из шести треугольников, поэтому его можно назвать гексафлексагоном, хотя у него нет шести сторон, и он не складывается. В связи с этим он интересен лишь как иллюстрация топологии³Мёбиуса, а не как представитель класса флексагонов.

б) дуогексафлексагон - представляет собой простой шестиугольник, вырезанный из бумаги. У него две стороны, и он также не складывается.

в) тригексафлексагон - шестиугольник, имеет три поверхности, сгибаем. Каждая поверхность имеет два варианта изображений. В результате имеем шесть различных изображений.

г) тетрагексафлексагон - шестиугольник, имеет четыре поверхности, сгибаем. Первая и вторая поверхности имеют по три варианта, третья и четвертая - по два. Всего различных изображений - десять.

д) пентагексафлексагон - шестиугольник, имеет пять поверхностей, сгибаем. Первая, вторая и третья поверхности имеют по три варианта, четвертая и пятая - по два. Всего различных изображений - тринадцать.

е) гексагексафлексагон - шестиугольник, имеет шесть поверхностей, сгибаем. В случае, когда флексагон изготовлен из прямой полоски бумаги, имеем пятнадцать различных изображений. Первая, вторая и третья поверхности имеют по три варианта, четвертая, пятая и шестая - по два.

Во втором случае, первая, вторая, третья и четвертая поверхности имеют по три варианта; пятая и шестая - по два. Всего шестнадцать изображений.

ж) гептагексафлексагон - шестиугольник, имеет семь поверхностей, сгибаем.

Первая, вторая, третья и четвертая поверхности имеют по три варианта; пятая, шестая и седьмая - по два. Всего восемнадцать изображений.

з) додекагексафлексагон - шестиугольник, сгибаем, имеет двенадцать поверхностей. Первая - шестая поверхности имеют по три варианта изображений; седьмая - двенадцатая имеют по два. Всего тридцать изображений.

Проверено утверждение, что слоев бумаги в двух соседних треугольных секциях всегда равно числу поверхностей данного флексагона.

В заключение все необходимые правила для сборки и изгибания были собраны вместе и оформлены, как «Рекомендации по изготовлению флексагонов»

Построение и исследования флексоров

Занимаясь изучением флексагонов, я узнал, что это изгибаемые многоугольники. А существуют ли изгибаемые многогранники (флексоры)? Оказалось, что этот вопрос занимал умы многих математиков. Как треугольник считается жёсткой геометрической фигурой, так пирамида – жёсткое геометрическое тело, его нельзя изменить, не сломав. Еще в 1766 году математик Эйлер высказал гипотезу: «Замкнутая пространственная фигура не допускает изменений, пока не рвется». В 1813 году французский математик Огюстен Луи Коши доказал, что выпуклый многогранник с данным набором граней и условиями их склейки единственен, то есть выпуклый многогранник изгибаемым не бывает. Н. П. Долбилин в своей статье «Жесткость выпуклых многогранников» писал: «Каждый, кто клеил или просто держал в руках картонную модель многогранника, замечал его жесткость и, возможно, задумывался над этим»⁴. Оказывается, эту версию можно опровергнуть. В статье В. Залгеллера «Непрерывно изгибаемый многогранник»⁵есть примеры изгибания замкнутого многогранника. Одним из таких примеров является построенный в 1977 году американским геометром Р. Коннели изгибаемый многогранник (рис.5), который и опроверг гипотезу Эйлера.

рис.5

Дж. М. Андреасом и Р. М. Сталкером независимо друг от друга было открыто семейство изгибаемых конечных многогранников с 2n вершинами, 6n ребрами (из которых 2n сдвоенные) и 4n треугольными гранями.Гранями многогранника являются грани определенного количества тетраэдров, соединенных между собой в циклическом порядке по определенным парам так, что получается фигура наподобие кольца. Число n может равняться 6, 8 и любому большему целому числу. При n = 6 эта фигура достаточно жесткая, но при n = 8 она уже может изгибаться и выворачиваться до бесконечности. Когда n четно, фигура стремиться принять симметричную форму. Когда n нечетно, из-за полного отсутствия симметрии картина становится еще более захватывающей. При n, большем или равном 22, кольцо может заузливаться.

Выкройка для построения таких колец оказалась несложной и чтобы построить для большего числа n, достаточно увеличить количество треугольников. В случае n = 6, нужно приготовить выкройку (рис.6), состоящую из 24 правильных треугольников и 9 клапанов. Вырезав её, нужно сделать сгибы по внутренним линиям (штриховые линии загнуть вверх, а пунктирные - вниз). Клапаны соединить и приклеить в соответствии с буквенными обозначениями⁶.

рис.6  

Единственный этап, на котором могут возникнуть трудности, приклеивание клапанов последнего тетраэдра (половина которого находится на одном конце развертки, а половина - на другом). Остальные тетраэдры складываются автоматически, если аккуратно согнуть развертку по всем линиям перед началом складывания. Так же модель флексора, состоящая из 6 тетраэдров достаточно жесткая, и не может изгибаться бесконечно. Этот недостаток можно исправить, если треугольники сделать не равносторонними, а равнобедренными. Таким образом, были построены кольца из 6, 8, 10, 11, 13 и 22 тетраэдров. Проверка показала, что:

n	количество вершин 2n	количество ребер всего 6n	количество сдвоенных ребер 2n	количество граней 4n
6	12	36	12	24
8	16	48	16	32
10	20	60	20	40
11	22	66	22	44
13	26	78	26	52
22	44	132	44	88

Внешне флексоры выглядят привлекательнее, чем флексагоны, но математический интерес вызывает только кольцо из 8 тетраэдров, которое по-другому называют магическим. Математик Ройал В. Хит на заготовке для кольца из 8 тетраэдров расставил числа от 1 до 32 следующим образом:

По этой заготовке изготавливается флексор. Он состоит из восьми тетраэдров. При вращении флексора, получаем четыре различные комбинации чисел с одним и тем же результатом:

1) 1+16+25+24+2+15+26+23=132; 2) 28+22+3+13+27+21+4+14=132;

3) 7+9+32+18+8+10+31+17=132; 4) 19+6+11+29+20+5+12+30=132;

Кроме этого, числа расположены так, что четыре грани каждого тетраэдра в сумме дают 66:

1) 1 + 30 + 7 + 28 = 66;

2) 12 + 17 + 14 + 23 = 66;

3) 31 + 4 + 26 + 5 = 66;

4) 21 + 15 + 20 + 10 = 66;

5) 2 + 29 + 8 + 27 = 66;

6) 11 + 18 + 13 + 24 = 66;

7) 32 + 3 + 25 + 6 = 66;

8) 22 + 16 + 19 + 9 = 66.

А также сумма граней при повороте по спирали равна132:

1) 1 + 22 + 32 + 11 + 2 + 21 + 31 + 12 = 132;

2) 25 + 13 + 8 + 20 + 26 + 14 + 7 + 19 = 132;

3) 24 + 6 + 9 + 28 + 23 + 5 + 10 + 27 = 132;

4) 16 + 30 + 17 + 4 + 15 + 29 + 18 +3 = 132;

5) 25 + 11 + 8 + 21 + 26 + 12 + 7 + 22 = 132;

6) 16 + 28 + 17 + 5 + 15 + 27 + 18 + 6 = 132;

7) 1 + 19 + 32 + 13 + 2 + 20 + 31 + 14 = 132;

8) 24 + 3 + 9 + 30 + 23 + 4 + 10 + 29 = 132.

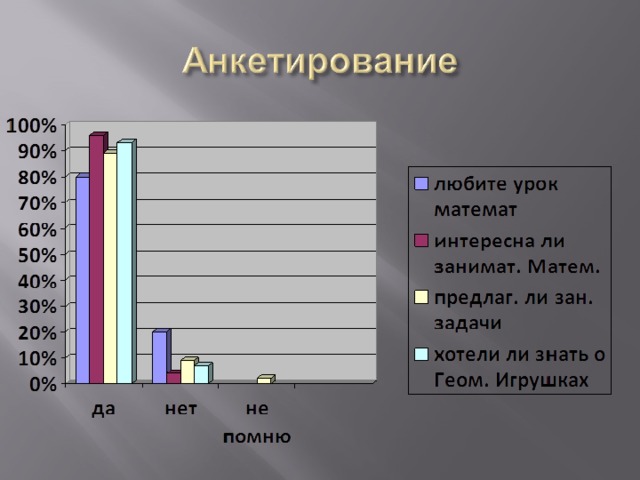
Анкетирование:

учащихся 4 «а» и 4 «б» классов МОУ СОШ №2

Всего в анкетировании приняли участие 46 человек.

Вопрос 1. Любите ли вы уроки математики?

«ДА» – 80%

«НЕТ» - 20%

Вопрос 2. Интересна ли вам занимательная математика?

«ДА» - 96%

«НЕТ» - 4%

Вопрос 3. В начальной школе на уроках математики учитель предлагал вам задания из занимательной математики?

«ДА» - 89%

«НЕТ» - 9%

«НЕ ПОМНЮ» - 2%

Вопрос 4. Хотели бы вы продолжить решать занимательные задачи?

«ДА» - 84%

Вопрос 5. Хотели бы что-нибудь узнать о геометрических игрушках?

«ДА» - 93%

«НЕТ» - 7%

Анализ анкет

На вопрос «Любите ли вы уроки математики?» ответ «да» дали 80%. Занимательная математика интересна 96 % школьников. 89 % пятиклассников помнят о том, что в начальной школе учителя предлагали им задания из занимательной математике, зато абсолютно все участники анкетирования хотели бы продолжить решать занимательные задачи в средней и старшей школе. Из всех анкетируемых 93 % пятиклассников хотели бы узнать, что такое геометрические игрушки.

Моя анкета была рассчитана на то, что ответом будет «да» или «нет», однако некоторые учащиеся поясняли свои ответы. Например: «Математика мне нравится, потому что она интересный предмет», «Математика – мой любимый предмет», «Занимательная математика расширяет кругозор», «Занимательные задачи лучше решать на каждом уроке», «В начальной школе нам предлагали магический квадрат», «Я никогда не слышал о геометрических игрушках, но очень хотел бы узнать» и др.

Таким образом, можно сделать вывод, что математика и занимательная математика интересны четвероклассникам МОУ СОШ №2, и в старшем и среднем звене стоит продолжать решать занимательные задачи и примеры. Ни один из учеников не написал, что знает что-нибудь о геометрических игрушках, но почти всем учащимся 4-х классов интересно узнать, что такое геометрические игрушки.

Результаты анкетирования доказывают, что наша исследовательская работа «Геометрические игрушки: флексагоны и флексоры» будет интересна школьникам.

Применение флексагонов и флексоров

В ходе выполнения проекта было ясно, что флексагоны и флексоры представляют собой занимательные головоломки и необычные игрушки. Но где ещё встречаются эти модели?

Оказалось, что флексагоныи флексоры могут быть основой творчества. Например, известно, что когда изобретатель флексагонов Артур Х. Стоун и его друзья создали и исследовали игрушку, они попутно придумали историю об одном джентльмене, у которого в флексагон попал кончик галстука. Порвать, любовно сделанную игрушку было жаль, и он продолжал играть, напрасно надеясь, что при очередном перегибании удастся освободиться. Эта сочиненная история легла в сюжет любительского фильма «Осторожно, математика!».

Изучив флексагоны и флексоры, мы смогли убедиться, что их можно использовать не только как интересные геометрические головоломки, но и найти им много других применений :

• Если каждый треугольник гексафлексагона раскрасить в свой цвет, то можно применять его для изучения цветов у детей дошкольного возраста. На каждом треугольнике можно поместить не только цвета, но и геометрические фигуры, рисунки животных, деревьев, цветов и др. На одном тригексафлексагоне разместятся 18 предметов одного вида, а на гексагексафлексагоне – 36. Таким образом, флексагон станет для ребенка не только забавной игрушкой, которую можно выворачивать, но и наглядным обучающим материалом.

• Флексагоны и флексоры можно применять на уроках математики, если на их сторонах написать числа и знаки «+», «-»,«×», «:». Выворачивая флексагон, можно числа складывать, вычитать, умножать и делить. Правда, при вычитании может получиться отрицательное число, а при делении – не всегда получится целое.

• Необычно применение флексагона в качестве шпаргалки. Написав на его сторонах формулы или правила, можно вывернуть флексагон обычными раскрашенными сторонами наружу. Такой полезный флексагон вешается на шею, как кулон, а в нужный момент разворачивается. Есть только опасность, что до нужной подсказки придется очень долго добираться, ведь известно, что 1, 2 и 3 стороны открываются в три раза чаще, чем 4, 5 и 6.

• Флексор можно использовать в качестве фоторамки. На все треугольники приклеиваются фотографии (например, учеников класса). Такой фоторамке не требуется специальная подставка.

• Флексагоны и флексоры можно подарить друзьям в качестве сувенира или во время проведения праздника научить их делать эти геометрические игрушки.

• Флексоры и простейшие флексагоны, раскрашенные в разные цвета или сделанные из фольги, можно использовать в качестве елочных украшений или обычного оформления праздника.

Заключение

Моя работа посвящена изучению свойств гнущихся многогранников, называемых флексагонами и флексорами, истории их возникновения и применению в обычной жизни.

Прочитав специальную литературу, изучив природу флексагонов и флексоров, изготовив их, можно сделать вывод: в их основе лежит чистая геометрия. Нельзя флексагоны и флексоры воспринимать как обычное оригами. Это выходит далеко за рамки привычного нам «бумаголомания» и является геометрией. Этим вопросом занимались несколько известных математиков, поэтому флексагоны и флексоры – это, с одной стороны, занимательная математика, а с другой, доказательство того, что существуют многогранники, обладающие способностью изгибаться и ломаться.

Мне было интересно заниматься этой работой, потому что, научившись практически изготавливать флексагоны и флексоры, я через геометрию занимательную погрузился в мир геометрии научной. Я познакомился с трудами известных математиков, изучил свойства треугольника и шестигранника, методику построения равностороннего треугольника и тетраэдра, изучил вопрос жесткости многогранников.

В работе изучен интерес к данной теме путем анкетирования четвероклассников, даны несколько советов практического применения флексагонов и флексоров, разработана брошюра «Практическое пособие по изготовлению флексагонов и флексоров». Моя работа предназначена тем, кто любит необычную и занимательную математику. Также работа может быть использована на уроках математики при изучении свойств треугольников, шестиугольников, тетраэдров.

«Несведущим в геометрии вход воспрещен», - гласила надпись над входом в помещение, где учил Платон. Для нашей работы эту надпись можно перефразировать: «Несведущим в геометрии вход разрешен».

Библиографический список:

1. Болл У., Коксетер Г. Математические эссе и развлечения. - М.: Мир, 1986, С. 471.

2. ВИКИПЕДИЯ. - URL:http://ru.wikipedia.org/wiki/Флексагон. Дата обращения: 1.11.2011.

3. ГарднерМ. Математические головоломки и развлечения. - М.: Мир, 1971, С. 235.

4. Дженкинс Д., Биар М. Математические головоломки. - М.: Центрполиграф, 2000, С. 32.

5. Долбинин Н. Жесткость выпуклых многогранников.// Квант. 1988. №5. С. 6 - 14.

6. Залгаллер В.Непрерывно изгибаемый многогранник. // Квант. 1978. № 9. С. 13 - 19.

7. Панов А. А. Флексагоны, флексоры, флексманы. //Квант. 1989. №1. С.10 -14.

8. Репина Г. Флексагоны как средство математического развития дошкольников. //Дошкольная педагогика. 2008. №3. С. 22-26.

9. Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. Учебное пособие для 5-6 классов.- М.: Мирос, 1995, С. 240.

10. Энциклопедия знаний. - URL: http://www.pandia.ru/96559/.Дата обращения: 1.11.2011.

Приложение №1

Опыты с равносторонними треугольниками

Два равносторонних треугольника = ромб

Три равносторонних треугольника = трапеция, у которой равны три стороны

Четыре равносторонних треугольника = параллелограмм, у которого каждая боковая сторона в два раза меньше основания

Шесть равносторонних треугольника = правильный шестиугольник

Приложение №2

Флексманы – существа, населяющие мир флексоров

Рисунок 1

Чтобы сделать флексман, вырежьте из плотной бумаги квадрат со сторонами 15 – 20 см. его нужно согнуть по диагоналям сгибом вверх и по штриховой линии (рисунок 1) сгибом вниз, а затем сложить, чтобы получился треугольник. Теперь надо проделать четыре одинаковые операции. Результат первой из них – сгиб по штриховой линии рисунка 2 – изображен на рисунке 3.

Рисунок 2

Рисунок 3

Остаются еще четыре завершающие операции – отгибание маленьких треугольников, и перед нами – флексман (рисунок 4).

Рисунок 4

1^ГарднерМ.Математические головоломки и развлечения. - М.: Мир, 1971, С. 11.

2^Август Фердинанд Мёбиус— немецкий математик и астроном-теоретик.

3^Топология— раздел математики, изучающий в самом общем виде явление непрерывности.

4^ Квант. 1988. № 5. С.6.

5^ Квант. 1978. № 9. С. 13-19.

6

Работу выполнил ученик 4А класса

Казаков Семен

Учитель математики : Кузнецова Е.И.

Задачи:

• изучить специальную литературу;
• изготовить и исследовать флексагоны и флексоры;
• представить в работе ряд математических игрушек, и показать, что в их основе лежит чистая математика;
• пробудить интерес школьников, продемонстрировав своей работой, что математика очень удивительный и необычный предмет для изучения.

Методы исследования:

Сбор информации, анализ периодической и научной литературы, точные расчеты при построении, создание наглядных моделей и конкретизация имеющегося материала.

Актуальность выбранной темы:

На первый взгляд, флексагоны и им подобные фигуры (обладающие удивительной способностью изгибаться, показывая новые грани) ‒ всего лишь игрушки. Но они сумели привлечь внимание в различных отраслях

Флексагон

многоугольник, сложенный из полоски бумаги прямоугольной или более сложной, изогнутой формы

Флексор

(от латинского flexor – сгибатель), представлен вращающимися кольцами тетраэдров

Рекомендации: сборку гексафлексагона нужно начинать с наибольшего числа и складывать так, чтобы треугольники, имеющие одинаковые числа, оказались наложенными друг на друга: все 7 на 7, затем 6 на 6, 5 на 5, 4 на 4, после чего получаем полоску из 10 треугольников и применяем схему сборки известную в научной литературе.

• 1. Построены: унагексафлексагон, дуогексафлексагон, тригексафлексагон, тетрагексафлексагон, пентагексафлексагон, гексагексафлексагон (двух видов), гептагексафлексагон, додекагексафлексагон и проведены исследования их поверхностей по схеме Таккермана.
• 2. Проверено: все перечисленные флексагоны являются шестиугольниками, и верно утверждение, что слоев бумаги в двух соседних треугольных секциях всегда равно числу поверхностей данного флексагона.
• 3. Разработана схема складывания для построения тетрагексафлексагон, пентагексафлексагона, гексагексафлексагона (второго вида), гептагексафлексагона и додекагексафлексагона.
• 4. Выпущена памятка: «Рекомендации по изготовлению флексагонов».

Только при правильной раскраске, можно увидеть все изображения одной и той же поверхности (до трёх видов у каждой поверхности). Для этого нужно разбить окрашиваемую поверхность на зоны А, В, С.

Сумма чисел на каждой

поверхности при вращении и при повороте по спирали равна числу 132.

• применяются как средство математического развития дошкольников и школьников младших классов
• выступают в роли игрушек и головоломок
• можно использовать в качестве фоторамки
• можно использовать флексагон в качестве шпаргалки.