По слайдам:Слайд 1. Тема моей работы- «Флексагоны, флексоры и флексманы».
Слайд 2: Цель моей работы: Создание своего изгибаемого многогранника ..
Для этого я решал следующие задачи:
-Подробно изучил мир многоугольников их свойства
- ознакомился с программой изготовления фигур
Слайд 3:Мир флексагонов очень разнообразен и доказывает ,что предмет математики очень серьёзен, но в то же время занимателен.
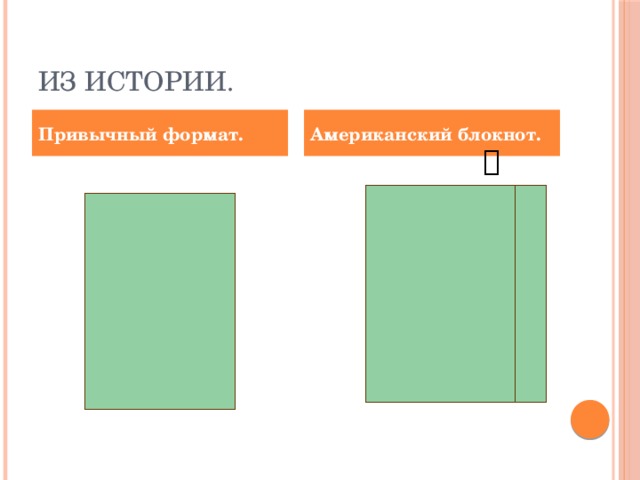
Слайд 4: придумать флексагоны помогло одно случайное обстоятельство - различие в формате английских и американских блокнотов.
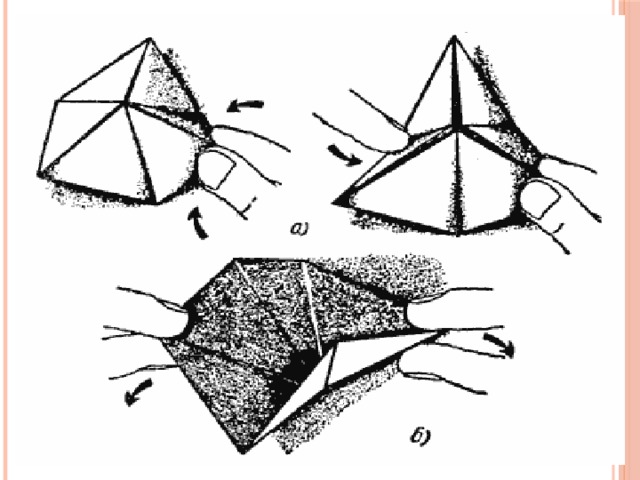
Однажды в конце 1939 года Артур Стоун,23-летний аспирант изучавшиц математику в Пристоне, обрезал листы американского блокнота под привычный формат.Из получившихся полосок он решил поскладывать разнообразные фигуры. Одна из сделанных им фигур оказалась особенно интересной. Перегнув полоску бумаги в трёх местах и соединив концы, он получил правильный шестиугольник.
Слайд 5: Взяв, этот шестиугольник, за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что когда шестиугольник раскрывался словно бутон, видимой становилась совсем другая поверхность. Был открыт самый первый флексагон!
Слайд 6:Существует 2 вида флексагонов гексафлексагоны(Шестиугольники) и тетрафлексагоны(четырехугольники).
Мной были начерчены развертки и выполнены следующие виды флексагонов.
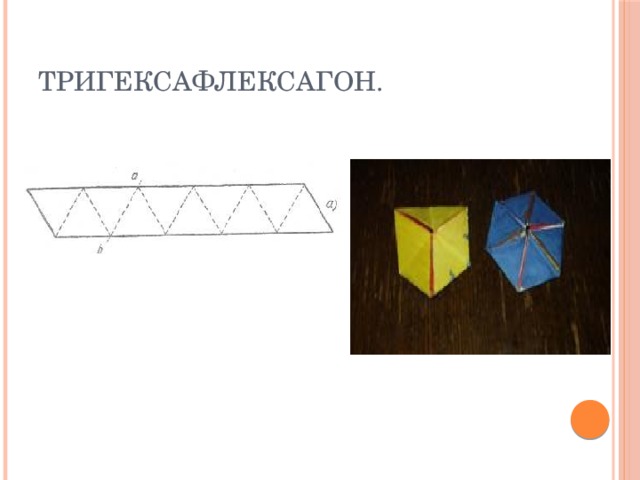
Слайд 7:Тригексафлексагон-имеет 3 поверхности. Наглядное изображение перед вами.
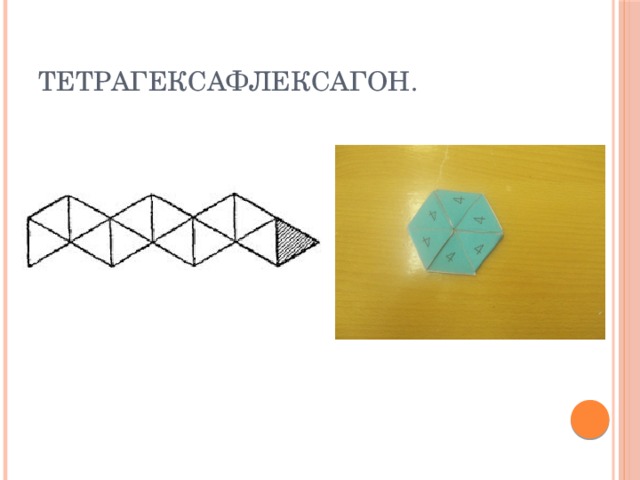
Слайд 8:Тетрагексафлексагон - имеет 4 поверхности. Вы можете увидеть его на слайде.
Слайд 9:Пентагексафлексагон - имеет 5 поверхностей.
Слайд 10: Гексагексафлексагон - имеет 6 поверхностей
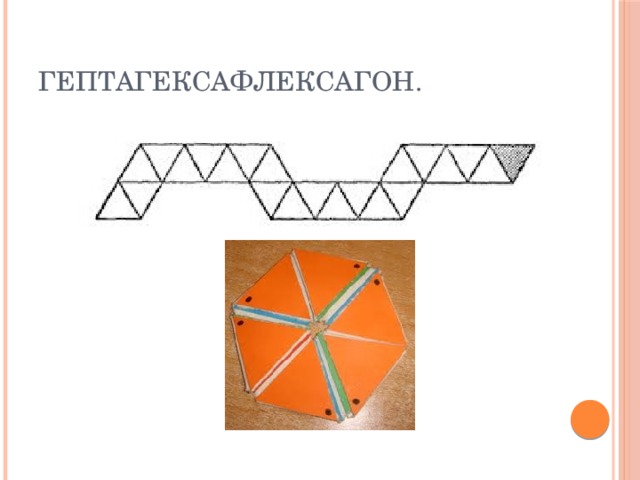
Слайд 11:Гептагексафлексагон - имеет 7 поверхностей
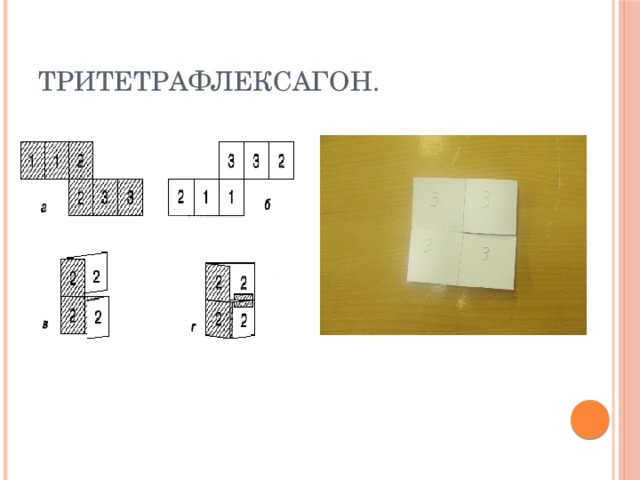
Слайд 12:Тритетрафлексагон - квадрат имеет 3 поверхности
Слайд13: Тетратетрафлексагон - прямоугольник имеет 4 поверхности
Слайд 14:Гексатетрафлексагон-квадрат имеет 6 поверхностей
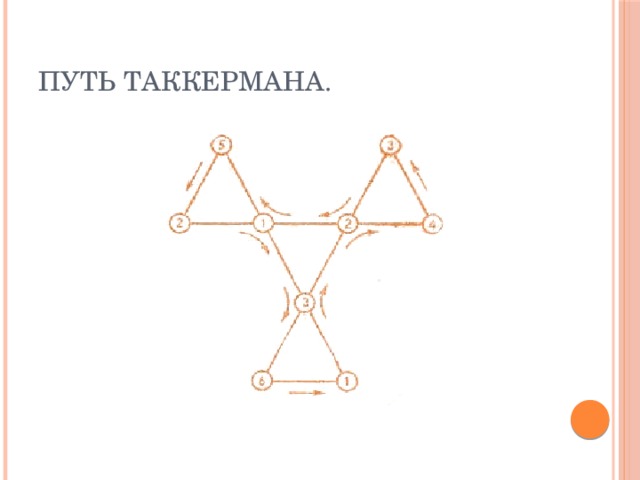
Слайд 15:На слайде вы видите схему разработанную Таккерманом для гексагексафлексагона. Им был найден простейший способ выявления всех поверхностей любого флексагона: держа флексагон за какой-нибудь угол, следует открывать фигуру до тех пор, пока она «открывается», а затем переходить к следующему углу. Этот метод так и называется «путь Таккермана». Он позволяет увидеть все шесть разворотов гексагексафлексагона за один цикл из 12 сгибаний. Стрелки указывают, в каком порядке становятся видимыми поверхности флексагона. Если модель перевернуть, то путь Таккермана будет изображаться той же схемой, но направление её обхода будет противоположным.
Исследуя флексагоны я узнал что существуют изгибаемые многоугольники, и тут я задался вопросом, а существуют ли изгибаемые многогранники.Оказалось существуют их называют флексорами.
Слайд 16:Флексоры - это вращающиеся кольца тетраэдров, имеющие 4 поверхности.
Мной было собрано два флексора
Слайд 17:Флексор с 6 ребрами
И …
Слайд18:флексор с 8ребрами
Слайд 19: Флексманы – это существа, населяющие мир флексагонов и флексоров.
Слайд 20: Самое примечательное свойство флексманов – это их умение ходить по наклонным плоскостям(под действием приложенной силы, он-флексман, совершает колебательные движения) Стоит поставить флексмана на достаточно пологую наклонную плоскость, и он тут же начинает мелкими шажками спускаться по ней. Каждый из флексманов обладает своеобразным характером или, уж во всяком случае, своеобразной походкой.
Слайд 21:Дальнейшее исследование темы, привели меня к изготовлению подобия куба йошимото. В кубе йошимото за основной элемент взят куб.
А я решил взять за главный элемент пирамиду.
Слайд 22:В процессе работы мне удалось создать свой непрерывно изгибаемый многогранник «СИМА»(собственный изгибаемый многогранник Абдыкулова).
Слайд 23:На этом слайде вы видите лишь часть Огромного мира Флексоров.
Слайд 24:.В основе работы тетрафлексагонов лежит двойное шарнирное соединение… которое повседневно встречаем в жизни….
Слайд 25: в декоративном творчестве…(открытки)
Слайд 26:В современном дизайне…
Слайд 27:Я предлагаю свои варианты …Как можно их еще использовать…(фоторамка ,люстра)
Слайд 28:(«Исследование создает новое знание»)
Я надеюсь, что многих заинтересует данная тема. И в процессе самостоятельной работы каждый может придти к открытию неизвестных до этого форм многогранников.Работа носит многоплановый развивающий характер, может быть использована в работе с детьми дошкольного и младшего школьного возраста.
Слайд 28: Спасибо за внимание!


 Блез Паскаль." width="640"
Блез Паскаль." width="640"