Тема: «Графы».
Цели урока:
изучение основных терминов теории графов
отработка навыков построения графов
1. Развивать навыки и умения применять математические методы для анализа, для работы с информацией в учебной деятельности и повседневной жизни
2. Способствовать развитию творческих навыков
1.Создание рабочей обстановки.
2.Воспитание активности и самостоятельности.
Оборудование: мультимедийный проектор, раздаточный материал, листы с домашним заданием.
План урока:
I. Орг. момент. (1 мин)
II. Актуализация знаний. (2 мин)
III. Теоретическая часть. (20 мин)
IV. Практическая часть. (15 мин)
V. Вопросы учеников. (3 мин)
VI. Д/з (2 мин)
VII. Итог урока. (2 мин)
Ход урока:
I. Организационный момент
Приветствие, проверка присутствующих, настрой на работу. Объяснение хода урока.
II. Актуализация знаний
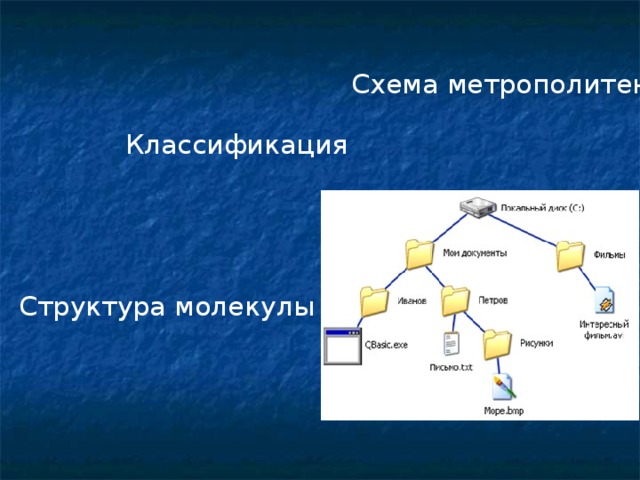
(1слайд) На доске записаны слова: классификация, молекулярная структура, схема метрополитена.
-Скажите, что, на ваш взгляд, общего между этими понятиями? (подвести к принципу изображения, к понятию графа).
III. Теоретическая часть
Изучение нового материала: Лекция с показом на проекторе.
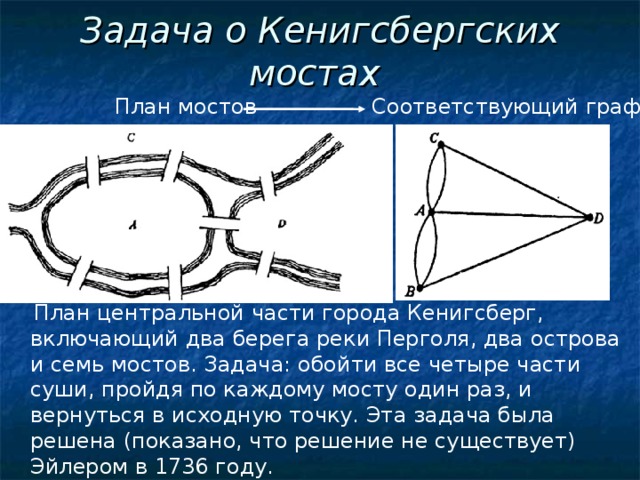
(2-5 слайд) Теория графов — одна из тех немногих математических теорий, для которых точно известен ее создатель, время и место создания: Леонард Эйлер, 1736 г.,
г. Петербург. Именно в этом году Л.Эйлером в “Записках Петербургской академии наук” была опубликована статья, в которой приводилось решение широко теперь известной задачи о Кёнигсбергских мостах. Разумеется, работа Л.Эйлера содержала не только отрицательный ответ на вопрос о возможности обойти все семь мостов г. Кёнигсберга так, чтобы по каждому из них пройти ровно один раз. В ней великий математик сформулировал и обосновал критерий, позволяющий отвечать на данный вопрос для любого графа.
Однако эта статья была единственной в течение почти столетия. Лишь в середине XIX века возродился интерес к теории графов. Исследование электрических сетей, структур молекул и строения кристаллов, применения к решению проблем в биологии и психологии послужили мощным катализатором в становлении данного раздела математики. Графы оказались удобным средством для описания самых разнообразных систем и явились эффективным инструментом структурного анализа. Графы успешно применяются для решения разнообразных задач планирования — выбор оптимального маршрута (транспортная задача), построение сетевого графика, исследование потоков в сетях и т.п. Одной из самых знаменитых задач, которая вызвала фейерверк остроумных работ в области теории графов, была предложенная де Морганом (около 1850 г.) проблема четырех красок: верно ли, что для раскраски любой карты так, чтобы граничащие между собой страны были раскрашены в разные цвета, достаточно четырех красок?
Теорема (о пяти красках)
Каждый планарный граф можно так раскрасить, используя пять цветов, что любые две смежные вершины будут окрашены в разные цвета.
А в 1850 году появились первые упоминания о гипотезе четырех красок, которая являлась улучшенной оценкой для планарных графов. Данная гипотеза была обоснована с помощью ЭВМ в 1976 году, а позже доказана аналитически и получила статус теоремы.
Теорема (о четырех красках)
Каждый планарный граф можно так раскрасить, используя четыре цвета, что любые две смежные вершины будут окрашены в разные цвета.
(6слайд) Применяется теория графов во многих науках. Многие физики, например, независимо друг от друга много раз открывали элементы теории графов заново.
Приведем ряд примеров приложений теории графов.
• «Транспортные» задачи, в которых вершинами графа являются пункты, а ребрами - дороги (автомобильные, железные и др.)
Другой пример - сети снабжения (энергоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, а ребрами - возможные маршруты перемещения (линии электропередач, газопроводы и т.д.).
• «Технологические задачи», в которых вершины отражают
производственные элементы (заводы, цеха, станки и т.д.), а дуги - потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков
• Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают участников обменной схемы (цепочки), а дуги - потоки материальных и финансовых ресурсов между ними. Задача заключается в
определении оптимальной цепочки обменов
• Управление проектами. С точки зрения теории графов проект - совокупность операций и зависимостей между ними.
• Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, а отношений между ними (например, отношений знакомства,доверия и т.д.) - в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия и др.
• Модели организационных структур, в которых вершинами являются элементы организационной системы, а ребрами или дугами - связи (информационные, управляющие, технологические и др.)
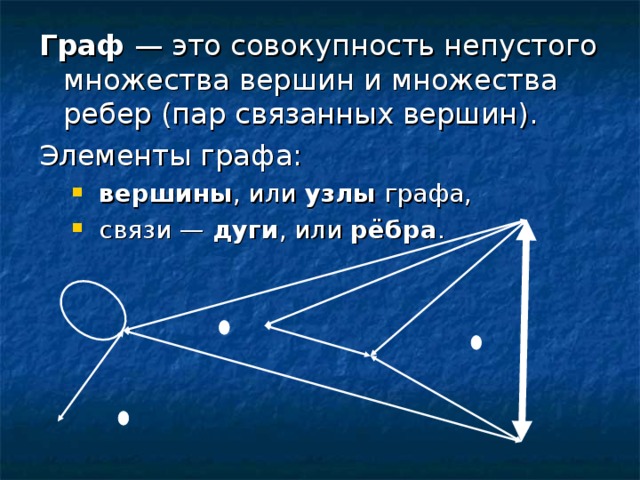
(7слайд) Итак, что же такое граф?
Граф — это конечная совокупность вершин, некоторые из которых соединены ребрами.. Если пара вершин соединена несколькими ребрами, — в этом случае говорят, что задан мультиграф, а такие ребра называют кратными.
Вершина называется изолированной, если она не является концом ни для одного ребра; висячей (или листом), если она является концом ровно одного ребра.
Петля – ребро, которое соединяет вершину саму с собой.
Если две различные вершины графа соединены ребром, то такие вершины называются смежными.
Количество ребер, выходящих из одной вершины, называется степенью этой вершины. Степень вершины а будем обозначать v(а).
Для петли будем считать, что это ребро выходит из вершины дважды.
Теорема 1. Сумма степеней всех вершин графа равна удвоенному числу его ребер.
Эта теорема доказывается совсем просто: легко видеть, что, когда подсчитывается сумма степеней всех вершин, каждое ребро в этой сумме фигурирует ровно два раза.
Теорема 2. Количество вершин нечетной степени любого графа всегда четно.
А “леммой о рукопожатиях” это утверждение называют из-за следующей интерпретации: в любой момент времени количество людей, сделавших нечетное число рукопожатий, четно. Действительно, если вершины графа — это люди, и вершины соединены ребром, если соответствующие два человека обменялись рукопожатием, то это одно и то же утверждение о получившемся графе.
Теорема 3. В любом графе есть по крайней мере две вершины, имеющие одинаковую степень.
Доказательство. Пусть в графе n вершин. Ясно, что степень каждой вершины может иметь значение от 0 до n – 1. Если степени всех вершин различны, то каждое из указанных значений должно реализоваться ровно для одной вершины. Рассмотрим вершины степени 0 и степени n – 1. Степень 0 означает, что эта вершина не соединена ни с какой другой; степень n – 1 означает, что эта вершина соединена со всеми другими вершинами. Но одновременно так быть не может.
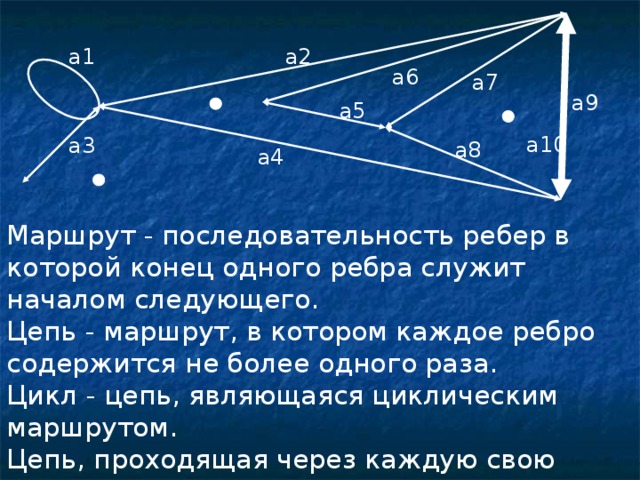
Маршрутом на графе называется последовательность ребер е1, е2, …, еk, в которой конец одного ребра служит началом следующего. Если при этом конец последнего ребра последовательности совпал с началом первого ребра, то маршрут называется циклическим.
Маршрут называется цепью, если каждое ребро содержится в нем не более одного раза. Цепь, являющаяся циклическим маршрутом, называется циклом.
Цепь, проходящая через каждую свою вершину ровно один раз, называется простой.
Если цикл является простой цепью, то он тоже называется простым.
Вершины А и В называют связанными, если существует цепь, начинающаяся в вершине А и заканчивающаяся в вершине В.
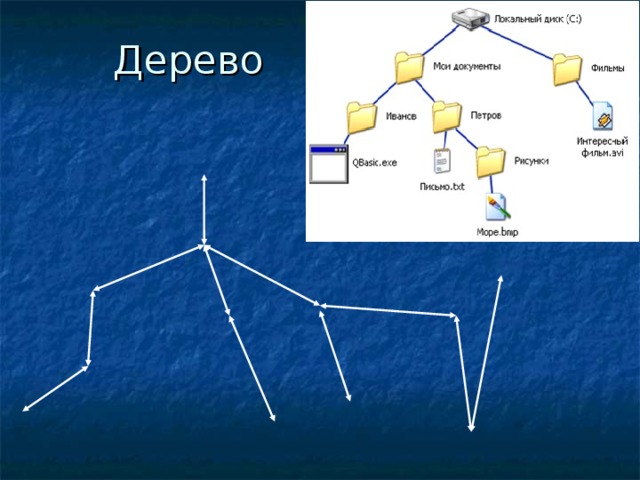
В теории графов деревом называется связный граф без циклов.
Дерево, как правило, изображают некоторым стандартным образом. Для этого фиксируют одну из вершин, ее называют корнем. Корень изображают внизу, а все остальные вершины распределяют по уровням. На первом уровне размещаются вершины, смежные с корнем, на втором — смежные с вершинами первого уровня, отличные от корня, на третьем — смежные с вершинами второго уровня, отличные от вершин первого уровня, и т.д.
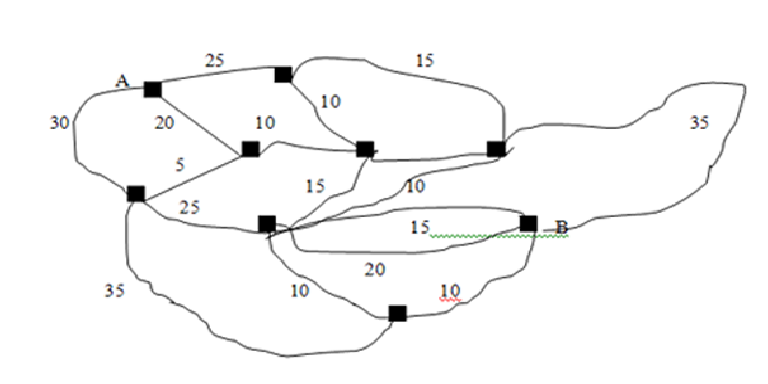
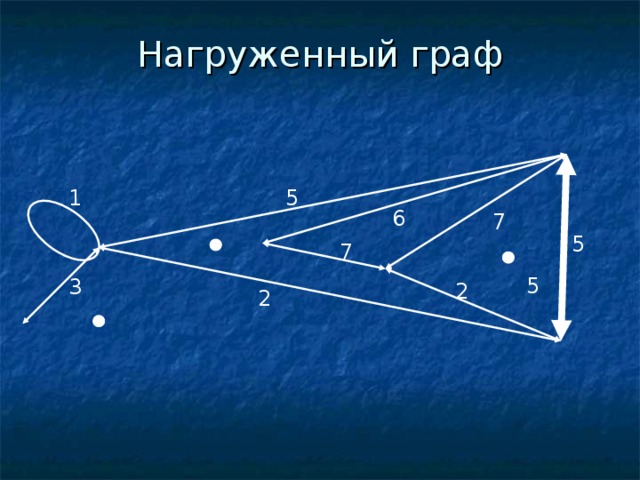
Нагруженным (взвешенным) графом называется такой граф, что его каждому ребру сопоставлено некоторое число (вес ребра).
Иногда бывает удобно рассматривать ненагруженный граф как нагруженный, у которого каждому ребру поставлено в соответствие число 1.
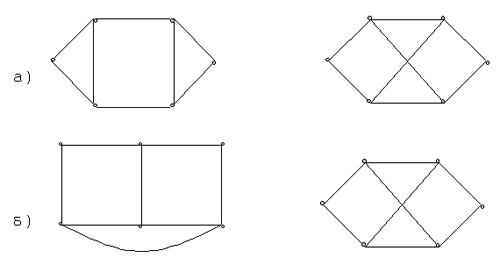
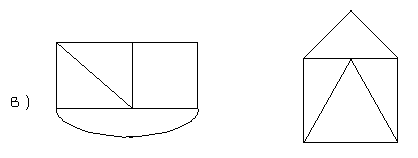
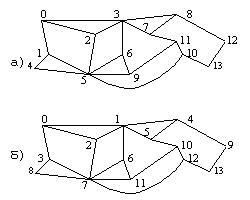
Практическая часть
У вас на столах материал для изучения. Ваша задача – распределить, кто какой способ задания графа(их описано несколько) изучает, после этого пояснить товарищам на примере. Далее - решение задач. Кто закончит - зовите, спрашиваю объяснение решения задачи у любого члена вашей группы.
Вопросы учеников
Ответы на вопросы учащихся.
Д/з Выучить определения по тетради(справочным материалам), решить задачи(на листе заданий).
Итоги урока
Подведение итогов урока. Выставление оценок.
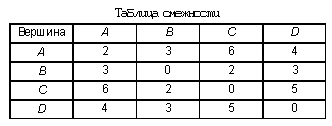
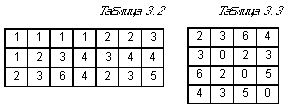
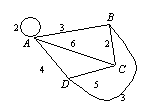 бычно граф задают одним из двух способов: перечислением всех его ребер или таблицей, где в клетке на пересечении строки и столбца, соответствующих данным вершинам, указано, соединены эти вершины ребром или нет. Такая таблица называется таблицей смежности. Если граф нагруженный, то для каждого ребра в соответствующей клетке указывается нагрузка.
бычно граф задают одним из двух способов: перечислением всех его ребер или таблицей, где в клетке на пересечении строки и столбца, соответствующих данным вершинам, указано, соединены эти вершины ребром или нет. Такая таблица называется таблицей смежности. Если граф нагруженный, то для каждого ребра в соответствующей клетке указывается нагрузка.