Основы логики

Основы логики

В пакет работ входят: презентация - теоретический материал по теме "Основы логики", практические задания на определение истинности составных высказываний и построение таблиц истинности, логические задачи, контрольная работа и тест на закрепление теоретических знаний по данной теме.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Алгебра логики 1 вариант»

Алгебра логики

1 вариант

1. Решите задачу

2. Выделите в сложных суждениях простые и обозначьте их буквами. Представьте эти сложные суждения в виде формул:

1.) После школы я поступлю или на экономический, или на юридический, или на факультет иностранных языков.

2.) Если завтра не будет дождя, то мы пойдем купаться на речку или пойдем собирать грибы в лес.

3. Составьте таблицы истинности для следующих формул:

1.) АВС

2.) А(АВ)

3.) (АВ)(ВА)

4.) (АВ)(АВ)(АВ)

4. Докажите с помощью таблиц истинности равносильность следующих логических выражений:

а) (А  В)  (А  );

б) (А  В)  (А&В)  ( & ).

Просмотр содержимого документа
«Алгебра логики 2 вариант»

Алгебра логики

2 вариант

Головы и ноги.

. Решите задачу

На лугу паслись лошади под присмотром пастухов. Если бы вы пожелали узнать, сколько всех ног на лугу, то насчитали бы 82 ноги. А если бы пересчитали головы, то оказалось бы, что всех голов – лошадиных человеческих – 26.

Сколько на лугу лошадей и сколько пастухов? Надо заметить, что ни безногих лошадей, ни калек-пастухов на лугу не было.

1.) Утром мы пойдем на рыбалку, позагораем, но уху варить не будем.

2.) Число 156 делится на 3 и 4, но не делится на 7.

3. Составьте таблицы истинности для следующих формул:

а) A  (B   )

б) A  (B   )

в) A  (B  )  A  (B  )

г) (А(ВС))(АВС)

4. Докажите с помощью таблиц истинности равносильность следующих логических выражений:

а) (А  В)  (А  );

б) (А  В)  (А&В)  ( & ).

Просмотр содержимого документа
«логические задачи»

Вариант № 1 лог/задачи

1. У Ивана машина красная, у Петра — не черная, не синяя, не голубая, у Михаила — черная и синяя, у Александра есть машины любого цвета (из всех выше перечисленных), у Бориса белого и синего цветов. У кого какого цвета машина, если все юноши были на машинах разного цвета?

2. На улице, встав в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя.

Девочка в зеленом платье — не Аня и не Валя — стоит между девочкой в голубом платье и Валей. Девочка в белом платье стоит между девочкой в розовом платье и Валей. Какого цвета платье у каждой из девочек?

Вариант № 2 лог/задачи

1. В бутылке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и молоко не в бутылке, сосуд с лимонадом находится между кувшином и сосудом с квасом, в банке — не лимонад и не вода. Стакан находится около банки и сосуда с молоком. Как распределены эти жидкости по сосудам?

2. В очереди за билетами в кино стоят: Юра, Миша, Володя, Саша и Олег. Известно, что: Юра купил билет раньше, чем Миша, но позже Олега. Володя и Олег не стояли рядом. Саша не находится рядом ни с Олегом, ни с Юрой, ни с Володей. Кто за кем стоит?

Вариант № 3 лог/задачи

1. На заводе работали три друга: слесарь, токарь и сварщик. Их фамилии Борисов, Иванов и Семенов. У слесаря нет ни братьев ни сестер. Он самый младший из друзей. Семенов, женатый на сестре Борисова, старше токаря. Назвать фамилии слесаря, токаря и сварщика.

2. Возле почты растут 6 деревьев: сосна, береза, липа, тополь, ель и клен. Какое из этих деревьев самое высокое и какое самое низкое, если известно, что береза ниже тополя, а липа выше клена, сосна ниже ели, липа ниже березы, сосна выше тополя?

Вариант № 4 лог/задачи

1. Три подруги вышли в белом, зеленом и синем платьях и туфлях. Известно, что только у Ани цвета платья и туфлей совпадали. Ни туфли, ни платье Вали не были белыми. Наташа была в зеленых туфлях. Определить цвета платья и туфель на каждой из подруг.

2. У меня три карандаша: желтый, коричневый и черный. Можно ли назвать самый короткий и самый длинный карандаш, если известно, что:

черный карандаш короче желтого, а желтый короче коричневого: желтый карандаш длиннее черного, а черный длиннее коричневого?

Вариант № 1 лог/задачи

2. На улице, встав в кружок, беседуют четыре девочки: Аня, Валя, Галя и Надя.

Вариант № 2 лог/задачи

Вариант № 3 лог/задачи

Вариант № 4 лог/задачи

черный карандаш короче желтого, а желтый короче коричневого: желтый карандаш длиннее черного, а черный длиннее коричневого?

Просмотр содержимого документа
«таблицы истинности»

Вариант № 1

Составьте таблицу истинности для формул:

(&) v (vB)&()

Проверьте равносильность таблиц истинности:

???

Вариант № 1

Составьте таблицу истинности для формул:

(&) v (vB)&()

Проверьте равносильность таблиц истинности:

Вариант №2

Составьте таблицу истинности для формул:

(AvB)&Bv(AvB)&C

Проверьте равносильность таблиц истинности:

???

Вариант №3

Составьте таблицу истинности для формул:

A&Bv(BvA)&Cv(B&C)

Проверьте равносильность таблиц истинности:

???

Вариант №2

Составьте таблицу истинности для формул:

(AvB)&Bv(AvB)&C

Проверьте равносильность таблиц истинности:

???

Вариант №4

Составьте таблицу истинности для формул:

(A&(B v C))&(A v B)

Проверьте равносильность таблиц истинности:

???

Вариант № 1

Составьте таблицу истинности для формул:

(&) v (vB)&()

Проверьте равносильность таблиц истинности:

???

Вариант №3

Составьте таблицу истинности для формул:

A&Bv(BvA)&Cv(B&C)

Проверьте равносильность таблиц истинности:

???

Вариант №2

Составьте таблицу истинности для формул:

(AvB)&Bv(AvB)&C

Проверьте равносильность таблиц истинности:

???

Вариант №3

Составьте таблицу истинности для формул:

A&Bv(BvA)&Cv(B&C)

Проверьте равносильность таблиц истинности:

???

Вариант №4

Составьте таблицу истинности для формул:

(A&(B v C))&(A v B)

Проверьте равносильность таблиц истинности:

???

Вариант №4

Составьте таблицу истинности для формул:

(A&(B v C))&(A v B)

Проверьте равносильность таблиц истинности:

???

Просмотр содержимого документа
«практические задания»

Определите истинность составных высказываний:

1. Найдите значения логических выражений:

а) (11)(10);

б) ((10)1)1;

в) (01)(10);

г) (0&1)&1;

д) 1&(1&1)&1;

е) ((10)&(1&1))&(01);

ж) ((1&0)(1&0))1;

з) ((1&1)0)&(01);

и) ((0&0)0)&(11).

2. Даны два простых высказывания:

А = {2  2 = 4}, В = {2  2 = 5}.

Какие из составных высказываний истинны:

а) ; б) ;

в) А & В; г) A  В;

д) А  В; е) А  В.

3. Даны простые высказывания:

А = {53}, В = {2=3} и С = {4

Определите истинность составных высказываний:

а) (A  B) & C  (A&C) (B&C);

б) (A&B)  C  (A  C) & (A  B).

4.. Даны простые высказывания:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Определите истинность составных высказываний:

а) (А&В)  (C  D); б) (А&В)  (C  D);

в) (А  В)  (C  D); г)  .

Постройте таблицы истинности алгебраически и с использованием электронных таблиц.

1: Построить таблицы истинности для следующих формул:

а) A  (B   )

б) A  (B   )

в) A  (B  )  A  (B  )

2: Докажите с помощью таблиц истинности равносильность следующих логических выражений:

а) (А  В)  (А  );

б) (А  В)  (А&В)  (&).

Просмотр содержимого презентации
«Элементы алгебры логики 9 класс»

ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ

МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИ

Турист шел к озеру. У перекрестка сидели двое парней, каждый из которых знал, какая дорога ведет к озеру. На вопросы они отвечали только «да» или «нет». Один из них всегда говорил правду, другой всегда лгал. Все это знал турист, но не знал, какая из двух дорог ведет к озеру.

Турист задал один вопрос одному из парней и узнал какая дорога ведет к озеру. Какой вопрос мог задать турист парню?

Турист задал два вопроса одному из парней и узнал какая дорога ведет к озеру. Какие вопросы мог задать турист парню?

Л огик а

Аристотель (384-322 до н.э.). Основоположник формальной логики (понятие, суждение, умозаключение).

Вильгельм Лейбниц (1646-1716). Основоположник математической логики (пытался построить первые логические исчисления: арифметические и буквенно-алгебраические).

Джордж Буль (1815-1864). Создал новую область науки - Алгебру логики (Булеву алгебру или Алгебру высказываний).

Высказывание

Высказывание - это предложение на любом языке, содержание которого можно однозначно определить как истинное или ложное .

В русском языке высказывания выражаются повествовательными предложениями:

Земля вращается вокруг Солнца .

Москва - столица.

Но не всякое повествовательное предложение является высказыванием:

Это высказывание ложное.

Побудительные и вопросительные предложения высказываниями не являются.

Без стука не входить!

Откройте учебники.

Ты выучил стихотворение?

Высказывание или нет?

На улице жарко.

Информатика – это наука.

Ура, снег пошел!

У треугольника 3 стороны и 3 угла.

Верно ли, что П=3,14 ?

Переведите число в десятичную систему.

Запишите домашнее задание

Простые и сложные высказывания

Высказывания бывают простые и сложные.

Высказывание называется простым , если никакая его часть сама не является высказыванием.

Пример: Завтра пойдет дождь. Я буду смотреть дома телевизор.

Сложные (составные) высказывания строятся из простых с помощью логических операций .

Пример: Если завтра пойдет дождь, то я буду смотреть дома телевизор.

Простые или сложные высказывания?

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Луна – спутник земли.

Студент запланировал выполнить следующие дела: подготовиться к зачету, побывать на тренировке, почитать интересную книгу, поиграть в шахматы.

Алгебра логики

Алгебра логики определяет правила записи, вычисления значений, упрощения и преобразования высказываний.

В алгебре логики высказывания обозначают буквами и называют логическими переменными .

Если высказывание истинно, то значение соответствующей ему логической переменной обозначают единицей ( А = 1 ), а если ложно - нулём ( В = 0 ).

0 и 1 называются логическими значениями .

Логические

операции

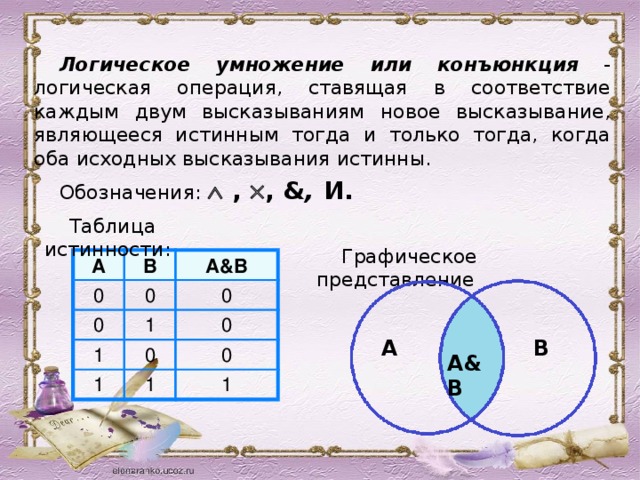
Логическое умножение или конъюнкция - логическая операция, ставящая в соответствие каждым двум высказываниям новое высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

Обозначения:  ,  , & , И.

Таблица истинности:

Графическое представление

А&В

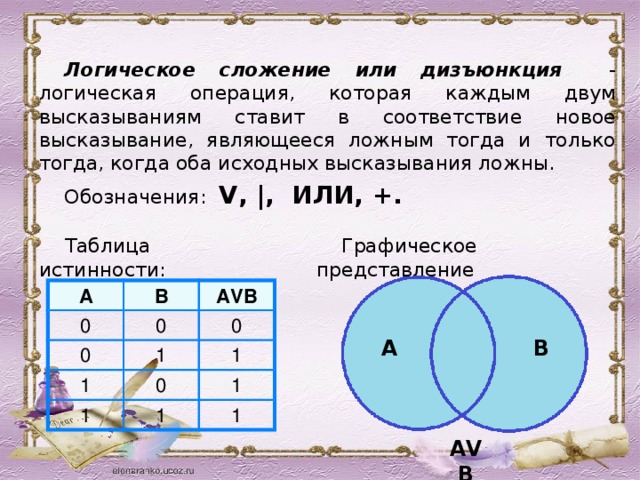
Логическое сложение или дизъюнкция - логическая операция, которая каждым двум высказываниям ставит в соответствие новое высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны.

Обозначения: V, |, ИЛИ, +.

Графическое представление

Таблица истинности:

АVВ

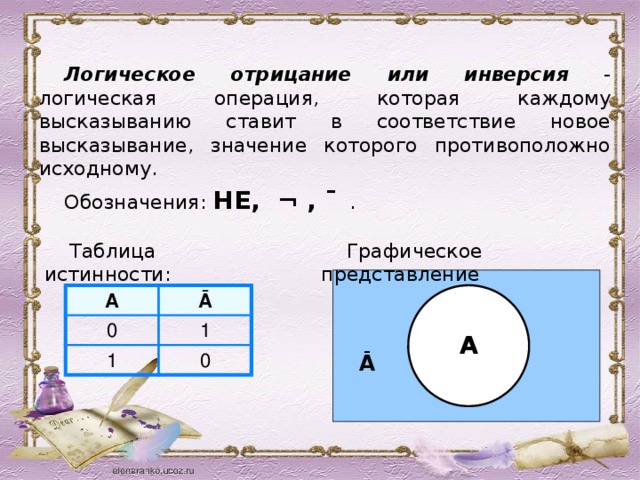
Логическое отрицание или инверсия - логическая операция, которая каждому высказыванию ставит в соответствие новое высказывание, значение которого противоположно исходному.

Обозначения: НЕ, ¬ , ¯ .

Таблица истинности:

Графическое представление

. Таблица истинности: А 0 В А - В 0 0 1 1 1 1 1 0 0 1 1" width="640"

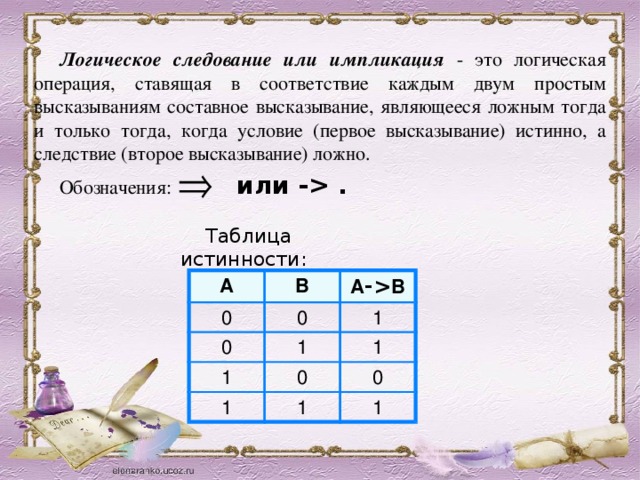
Логическое следование или импликация - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Обозначения: или - .

Таблица истинности:

А - В

В 0 0 1 1 1 1 0 0 0 1 1" width="640"

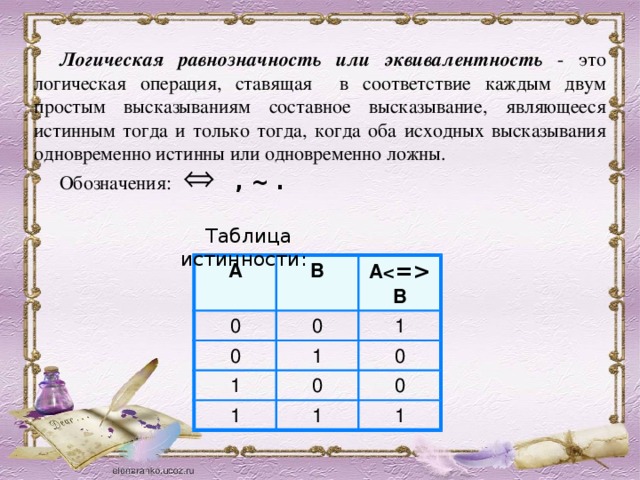
Логическая равнозначность или эквивалентность - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

Обозначения: , ~ .

Таблица истинности:

А = В

ЭЛЕМЕНТЫ АЛГЕБРЫ ЛОГИКИ

Повторение
Объясните, почему следующие предложения не являются высказываниями:
Какого цвета этот дом?
Число Х не превосходит единицы.
Пейте томатный сок!
Эта тема скучна.
Приведите примеры истинных и ложных высказываний из биологии, истории, литературы.

Повторение
В следующих высказываниях выделите простые высказывания, обозначив каждое из них буквой; запишите с помощью букв и знаков логических операций каждое составное высказывание.

Число 376 четное и трехзначное.
Зимой дети катаются на коньках или на санках или на лыжах.
Неверно, что Солнце движется вокруг Земли.

Порядок выполнения логических операций в сложном логическом выражении
1.Инверсия; 2. Конъюнкция; 3. Дизъюнкция; 4. Импликация; 5. Эквивалентность.

Повторение
Пусть
А=«Ане нравятся уроки математики», а
В=«Ане нравятся уроки химии». Выразите следующие формулы на обычном языке.

А&В АvB (А&В)
А&В АvB (АvB)
А&В АvB (А&В)
$Определите истинность составного высказывания: (А&В) & ( C \/ D ), состоящего из простых высказываний: А = {Принтер – устройство вывода информации}, В = {Процессор – устройство хранения информации}, С = {Монитор – устройство вывода информации}, D = {Клавиатура – устройство обработки информации}. Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С = 1, D = 0. Определим теперь истинность составного высказывания, используя таблицы истинности логических операций: ( 1 & 0 ) &(1 \/ 0) = (0 & 1) & (1 \/ 0) = 0 Составное высказывание ложно.$
Определите истинность составного высказывания:

(А&В) & ( C \/ D ), состоящего из простых высказываний:
А = {Принтер – устройство вывода информации},
В = {Процессор – устройство хранения информации},
С = {Монитор – устройство вывода информации},
D = {Клавиатура – устройство обработки информации}.

Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний:
А = 1, В = 0, С = 1, D = 0.
Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:
( 1 & 0 ) &(1 \/ 0) = (0 & 1) & (1 \/ 0) = 0
Составное высказывание ложно.
( C v D ); в) ( А v В )  ( C & D ); г) А  B ." width="640"
Даны простые высказывания:
А = {Принтер – устройство ввода информации},
В = {Процессор – устройство обработки информации},
С = {Монитор – устройство хранения информации},
D = {Клавиатура – устройство ввода информации}.

Определите истинность составных высказываний:

а) ( А & В ) & ( C v D );
б) ( А & В ) = ( C v D );
в) ( А v В )  ( C & D );
г) А  B .
$Определите истинность составных высказываний:         а) (1 \/ 1) \/ (1 \/ 0);         б) ((1 \/ 0) \/ 1) \/ 1;         в) (0&1)&1;         г) 1&(1&1)&1;         д) ((1 \/ 0)&(1&1))&(0 \/ 1);         е) ((1&1) \/ 0)&(0 \/ 1); .        ж) ((1&0) \/ (1&0)) \/ 1;         з) ((0&0) \/ 0)&(1 \/ 1)$

Определите истинность составных высказываний:

        а) (1 \/ 1) \/ (1 \/ 0);
        б) ((1 \/ 0) \/ 1) \/ 1;
        в) (0&1)&1;
        г) 1&(1&1)&1;
        д) ((1 \/ 0)&(1&1))&(0 \/ 1);
        е) ((1&1) \/ 0)&(0 \/ 1); .
       ж) ((1&0) \/ (1&0)) \/ 1;
        з) ((0&0) \/ 0)&(1 \/ 1)


Построение таблиц истинности

Построение таблиц истинности
для логических выражений
подсчитать n - число переменных в выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2 n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью

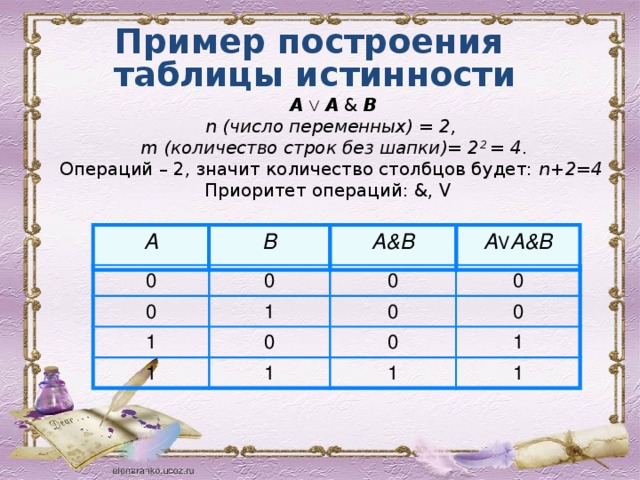
Пример построения
таблицы истинности
А V A & B
n (число переменных) = 2,
m (количество строк без шапки)= 2 2 = 4 .
Операций – 2, значит количество столбцов будет: n+2=4
Приоритет операций: &, V
A
B
A&B
A V A&B
0
0
0
1
0
1
0
1
0
0
0
0
1
1
1
1

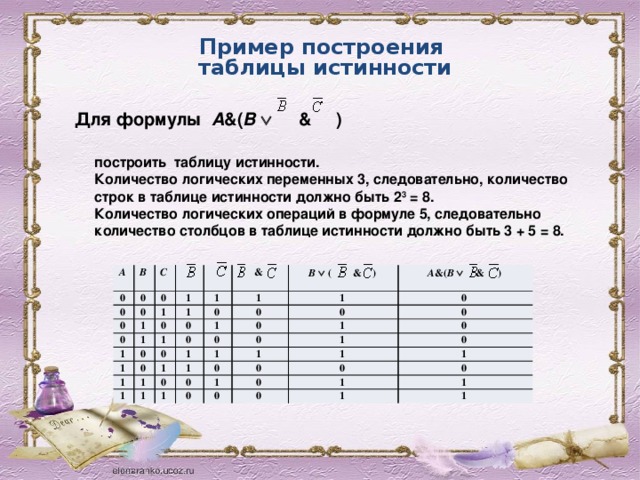
Пример построения
таблицы истинности
Для формулы A &( B Ú & )
построить таблицу истинности.
Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2 3 = 8.
Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.
A
0
B
0
C
0
0
0
0
0
1
1
1
0
1
&
1
1
1
1
1
B Ú ( & )
0
0
0
1
A &( B Ú & )
1
0
1
0
0
0
1
1
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
0
1
0
1
0
1
0
0
1
0
0
0
1
0
0
1
1
1
1
2)&(X5) Х 2 А (X2) 3 0 A 4 1 1 B ( X5) A&B 0 1 0 5 0 0 0 1 0 0 0 0 0 0" width="640"
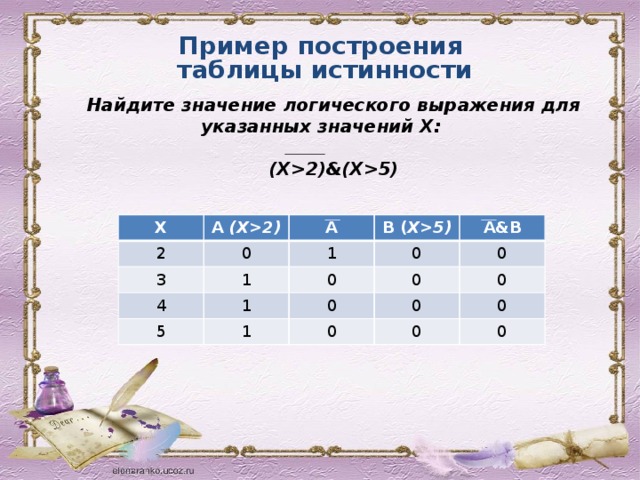
Пример построения
таблицы истинности
Найдите значение логического выражения для указанных значений Х:

(X2)&(X5)
Х
2
А (X2)
3
0
A
4
1
1
B ( X5)
A&B
0
1
0
5
0
0
0
1
0
0
0
0
0
0

Построить таблицы истинности
В & (А V В) А & (В V В)
А & В & С
F=(AVB) & (AVB)
Постройте таблицы истинности:
А) (А В) V В
В) (А & В) (А V (А & В))
С) (А (В С)) (А & В & С)