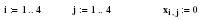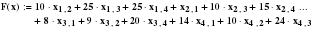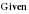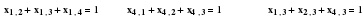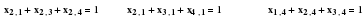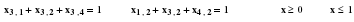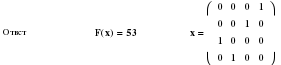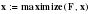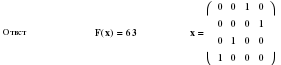Анализ сложных технических и организационных систем

Сложность систем

Различают три типа систем по сложности. К первому относятся системы с четко выраженной иерархией (соподчиненностью). Их будем называть не очень сложные системы. Например. Телефонная сеть какого-либо города. Эти системы поддаются математическому описанию. Ко второму типу относятся системы, которые не поддаются математическому описанию, либо те системы, для которых математический аппарат еще не разработан. Это очень сложные системы. В третьем типе систем отчетливо просматривается присутствие «человеческого фактора», обладающего своими скрытыми, целями. Каждый человек имеет свои личные цели, которые не всегда совпадают с целями системы, в которую они входят. Часто эти цели не ясны другим людям, и, прежде всего руководителям системы. Поэтому часто такие системы оказываются не эффективными и их цель не бывает достигнута вообще или в полной мере. Чтобы такие системы были эффективными, необходимо учитывать и интересы входящих в эту систему людей. Если руководитель некоторого предприятия не будет учитывать интересы своих работников, не будет заботиться о них, то такое предприятие не сможет работать достаточно эффективно. Системы этого типа называют сверхсложными системами.

Заметим, что система, включающая не большое количество людей, имеет немного связей, но она будет сверхсложной системой. Поэтому следует сделать уточнение: простыми будем называть те системы, в которых количество связей относительно не велико и нет ярко выраженного человеческого фактора.

Важно отметить, что простые и сложные системы подвергаются научному исследованию, а для сверхсложных систем соответствующий исследовательский аппарат еще не разработан. Заметим также, предложенная классификация систем по степени сложности не является достаточно полной и строгой.

Графы

Вы узнаете:

• что такое граф, вершина, ребро, дуга;

• что такое сеть, структура, параметры дуг;

• как решаются такие задачи.

Геометрия, занимающаяся графическим представлением объектов, благодаря своей наглядности, получила широкое распространение еще в древности. Наглядность геометрии используется при анализе сложных технических и организационных систем. Граф - совокупность вершин и ребер. Каждую вершину обозначают порядковым номером. Если ребро графа имеет направление, то его называют дугой. Сеть – это граф, в котором вершины соединены дугами. Сеть характеризуется структурой и параметрами дуг.

1 2 1 2

i Д _i,j j

граф дуга сеть

4 3

4 3

Структура сети (топология) показывает, какие вершины связаны между собой и каково направление связывающих дуг. Дугу обозначают двойной индексацией:

• i - номер вершины, из которой выходит дуга.

• j - номер вершины, в которую входит дуга.

Каждая дуга может иметь свою характеристику.

Например. Tij – продолжительность движения по дуге i-j.

Например. Cij - стоимость перемещения по дуге i-j.

Например. Dij - пропускная способность по дуге i-j.

Зная структуру сети и характеристики её дуг, можно решать различные задачи оптимизации, достаточно часто встречающиеся на практике.

Задача о коммивояжере.

Есть 4 пункта соединенных дорогами между собой каждый с каждым, т.е. из любого пункта можно проехать в любой другой пункт. Время, необходимое для переезда из одного пункта в другой см. в таблице.

Требуется найти такой маршрут, начинающийся в данном пункте, проходящий через все пункты и заканчивающийся в точке выезда, чтобы его продолжительность была наименьшей.

Таблица

Экономико-математическая модель задачи:

Из пункта 1 можно выехать в любой пункт 2-3-4 х₁₄ 1 х₁₂

x₁₂+x₁₃+x₁₄=1 Условие выезда из пункта 1

x₂₁+x₂₃+x₂₄=1 Условие выезда из пункта 2

x₃₁+x₃₂+x₃₄=1 Условие выезда из пункта 3 х₁₃

x₄₁+x₄₂+x₄₃=1 Условие выезда из пункта 4

В пункт 1 можно въехать в любой пункт 2-3-4 х₄₁ 1 х₂₁

x₂₁+x₃₁+x₄₁=1 Условие въезда в пункт 1

x₁₂+x₃₂+x₄₂=1 Условие въезда в пункт 2

x₁₃+x₂₃+x₄₃=1 Условие въезда в пункт 3 х₃₁

x₁₄+x₂₄+x₃₄=1 Условие въезда в пункт 4

х_ij =0; Условие не отрицательности решения i=1…4; j=1…4

Требование минимальной продолжительности маршрута запишем в виде ЦФ, где коэффициенты при переменных – это время в пути между пунктами.

F=10x₁₂+25x₁₃+25x₁₄+x₂₁+10x₂₃+15x₂₄+8x₃₁+9x₃₂+20x₃₄+14x₄₁+10x₄₂+24x₄₃

Результаты решения на компьютере:

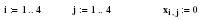
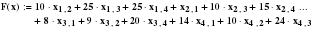
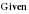
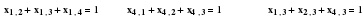
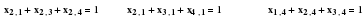
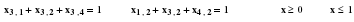
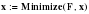
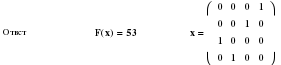
х₁ х₄ х₂ х₃ х₁ маршрут движения

25 10 10 8 время в пути = 53

Максимальной продолжительности путь.

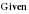
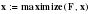
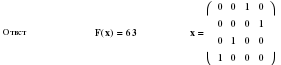
х₁ х₃ х₂ х₄ х₁ маршрут движения

25 9 15 14 время в пути = 63

К задачам коммивояжера можно свести значительное число различных практических задач:

• выбор маршрута при развозке грузов;

• последовательность обработки различных деталей на одном станке;

• проектирование технологических процессов и т.д.

Вы узнали:

• что такое сеть, структура сети и параметры дуг;

• как решать такого класса задачи