Представление числовой информации в различных системах счисления.
Цель: научить учащихся выполнять арифметические действиями в двоичной системе счисления.
Задачи:
образовательные:
- повторение и закрепление знаний учащихся о системах счисления;
- формировать у школьников умение выполнять правильно арифметические действия в двоичной системе счисления;
развивающие:
- развивать логическое мышление учащихся;
- развивать познавательный интерес учеников.
Содержание нового материала: правила сложения, умножения, вычитания и деления в двоичной системе счисления.Правила перевода чисел из одной системы счисления в другую.
Как только люди стали общаться, т.е. передавать информацию, они стали считать. Первыми инструментами счета были пальцы рук и простые предметы, например, камешки. Слово "камешки" по латыни CALCULI, а их перебрасывание при счете - CALCULARE, что и означает "считать". Отсюда - "калькулятор".
Затем расчеты стали фиксировать, что привело к появлению систем счисления.
Система счисления - это свод приемов обозначения и записи чисел при помощи специальных символов - цифр.
Системы счисления можно разделить:
- непозиционные системы счисления;
- позиционные системы счисления.
Сначала люди придумали непозиционные или кодовые системы счисления (IV тысячелетие до н.э.), в которых расположение цифр в числе не имеет значения и для обозначения каждого числа существует свой символ.
Пример 1. У многих народов использовалась система, алфавит которой состоял из одного символа — палочки. Для изображения какого-то числа в этой системе нужно записать определенное множество палочек, равное данному числу: ||||| — число пять.
Но в непозиционных системах трудно записывать большие числа и выполнять арифметические действия. Более совершенной системой (переходной от непозиционных систем к позиционным) стала - римская (500 лет до н.э.), которая применяется и в наше время. Алфавитом (цифрами) этой системы служат символы:
I (1)
V (5)
X (10)
L (50)
C (100)
D (500)
M (1000)
Здесь уже положение цифры в числе меняет ее значение. Например, в числе IV I отнимается от V, а в числе VI - прибавляется к V. Число 1995 в этой системе запишется так: MCMXCV.
Но и этой системе присущи все недостатки непозиционных систем. Чтобы от них избавиться понадобились позиционные системы.
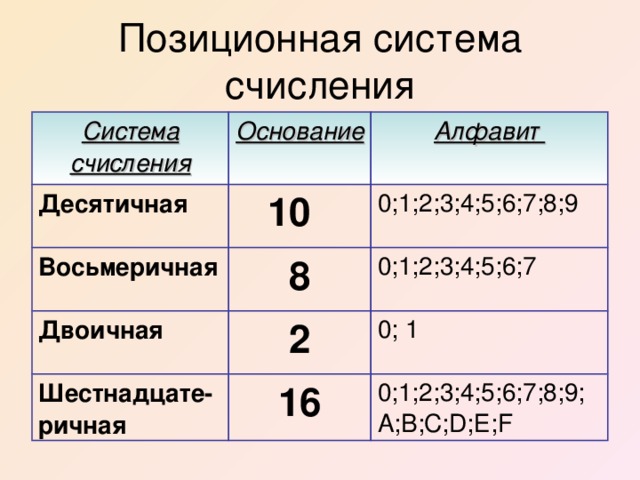
Если место, занимаемое символом в записи числа, придает этому символу определенное значение, то такая система счисления называется позиционной.
Количество цифр системы (символов алфавита) называется ее основанием, место цифры в числе - разрядом, а количество цифр в числе - его разрядностью.
Самой древней известной позиционной системой счисления считают вавилонскую шестидесятеричную. Следы ее сохранились до наших дней в единицах измерения времени и угловых величин. Но наибольшее распространение получила и имеет до сих пор индо-арабская ДЕСЯТИЧНАЯ СИСТЕМА (VI в). Возможно, она наиболее естественна для человека, т.к. считать мы учимся на пальцах, а их на двух руках как раз 10. В этой системе 10 цифр: от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз.
Любое число может быть представлено в виде суммы, где каждое слагаемое представляет собой произведение коэффициента (цифры числа) на основание системы (10) в степени, равной разряду этой цифры.
Позиция цифры в числе называется разрядом.
Aq = an-1´qn-1 + … + a1´q1 + a0´q0 + a-1´q-1 + … + a-m´q-m, где
q — основание системы счисления (количество используемых цифр)
Aq — число в системе счисления с основанием q
a — цифры многоразрядного числа Aq
n (m) — количество целых (дробных) разрядов числа Aq
Пример: 239,4510 = 2´102 + 3´101 + 9´100 + 4´10-1 + 5´10-2.
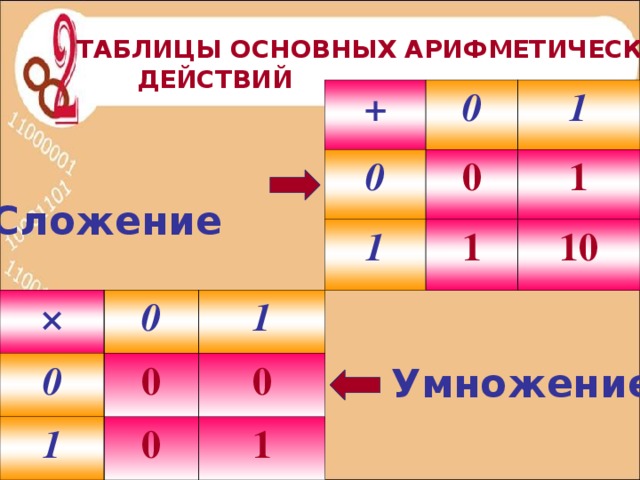
Правила сложения:
0+0=0
0+1=1
1+0=1
1+1=10
Обратить внимание учащихся на то, что при сложении двух единиц в двоичной системе счисления в записи получается 0, а единица переносится в следующий разряд. При сложении трех единиц получается в записи 1, и единица переносится в следующий разряд. (1+1+1=11).
Пример 1.
101+10=111
Учащиеся самостоятельно решают следующие примеры:
1001+11=1100
110+110=1100
Правила умножения:
0*0=0
0*1=0
1*0=0
1*1=1
Пример 1.
101*11=1111
Объяснение:
Каждую цифру второго множителя умножаем на каждую цифру первого множителя, результаты произведений складывают между собой по правилам сложения в двоичной системе счисления. (Математика - 3 класс).
Учащиеся самостоятельно решают следующие примеры:
1001*101=101101
1001*11=11011
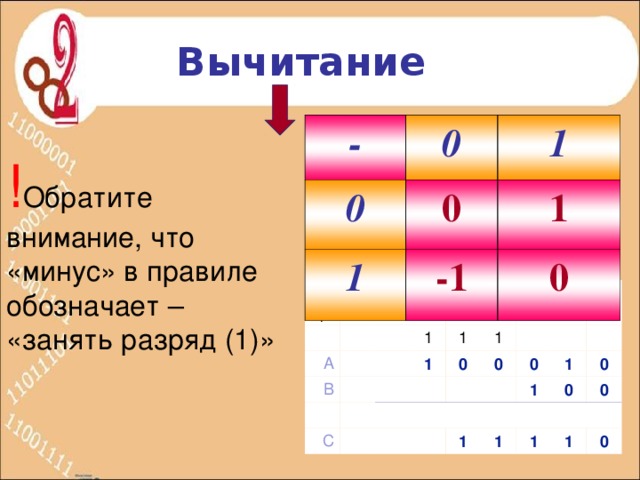
Правила вычитания:
0-0=0
1-0=1
1-1=0
0-1=-1
Обратить внимание учащихся на то, что «минус» в последнем правиле обозначает – «занять разряд (1)».
Пример 1.
10110-111=1111
Объяснение:
Вычитание выполняется так же, как в математике. Если цифра в уменьшаемом меньше цифры вычитаемого, то для данного вычитания необходимо занять разряд (1), т.к. 10-1=1. Если слева от такого вычитания стоит 0, то мы не можем занять разряд. В этом случае разряд занимаем в уменьшаемом у близстоящей слева от данного вычитания единицы. При этом все нули, у которых мы не могли занять разряд, необходимо поменять на единицу, т.к. 0-1=-1. Желательно все изменения в цифрах записывать сверху данного вычитания. Дальнейшее вычитание выполнять с получившимися сверху цифрами.
Пример 2.
100000-11=11101
Учащиеся самостоятельно решают следующие примеры:
100010-100=
101011-10111=
Правило деления:
Деление выполняется по правилам математики, не забывая, что мы выполняем действия в двоичной системе счисления.
Пример 1.
101101:1001=101
Объяснение:
В частном смело пишем первую 1, т.к. число в двоичной системе не может начинаться с 0. Умножаем эту 1 на делитель, результат правильно записываем под делимом, соблюдая разрядность. Выполняем вычитание по правилам вычитания в двоичной системе счисления. Сносим следующую цифру делимого, и полученное число сравниваем с делителем. В данном случае – полученное число меньше делителя, в частном записываем 0 (в противном случае – 1). Сносим следующую цифру делимого. Получили число равное делителю, в частном записываем 1, и т.д.
Примеры для самостоятельного решения:
1001000:1000=1001
111100:1010=110
Число 555 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой записи, что уже не замечаем, как в уме умножаем цифры числа на разные степени числа 10. Это число в развернутой форме будет выглядеть так:
55510 = 5 · 102 + 5 · 101 + 5 · 100 , откуда видно, что число в позиционной системе записывается в виде суммы числового ряда степеней основания ( в нашем случае это 10), в качестве коэффициентов которых выступают цифры данного числа.
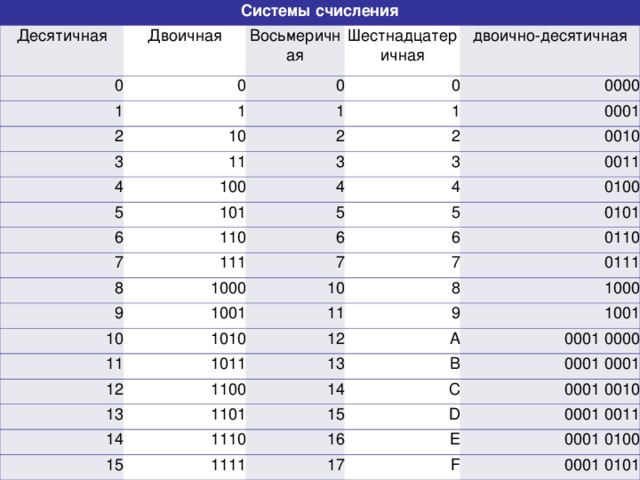
Теперь запишем двоичное число, которое может состоять только из нулей и единиц, например, 11112 в развернутом виде:
11112 = 1 · 23 + 1 · 22 + 1 · 21 + 1 · 20 .
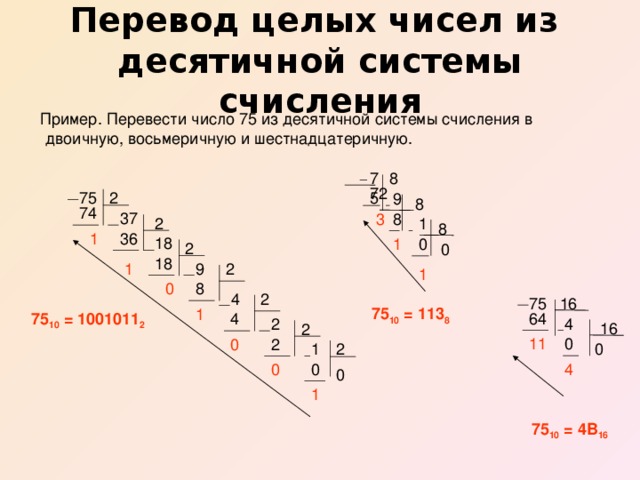
Перевод числа из десятичной системы в систему счисления c другим основанием:
- Последовательно выполнять деление исходного целого числа на основание той системы, в которую переводим, пока не получится частное меньшее делителя.
- Записать полученные остатки в обратном порядке, начиная с последнего частного.
ПЕРЕВОД чисел в десятичную систему счисления выполнить довольно легко. Для этого необходимо записать число в развернутой форме и вычислить его значение в десятичном виде.
Самостоятельная работа
1 вариант
1)Заданы двоичные числа X и Y.
Вычислите X+Y и X–Y, если: X=1000111, Y=11010
2) Заданы двоичные числа X и Y.
Вычислите X+Y–1001101, если: X=1010100, Y=110101
3) Заданы двоичные числа X и Y.
Вычислите X*Y и X:Y, если: X=11001, Y=101
2 вариант
1)Заданы двоичные числа X и Y.
Вычислите X+Y и X–Y, если: X=100111, Y=1101
2) Заданы двоичные числа X и Y.
Вычислите X+Y–1001101, если: X=100111, Y=1101
3) Заданы двоичные числа X и Y.
Вычислите X*Y и X:Y, если: X=100111, Y=1101