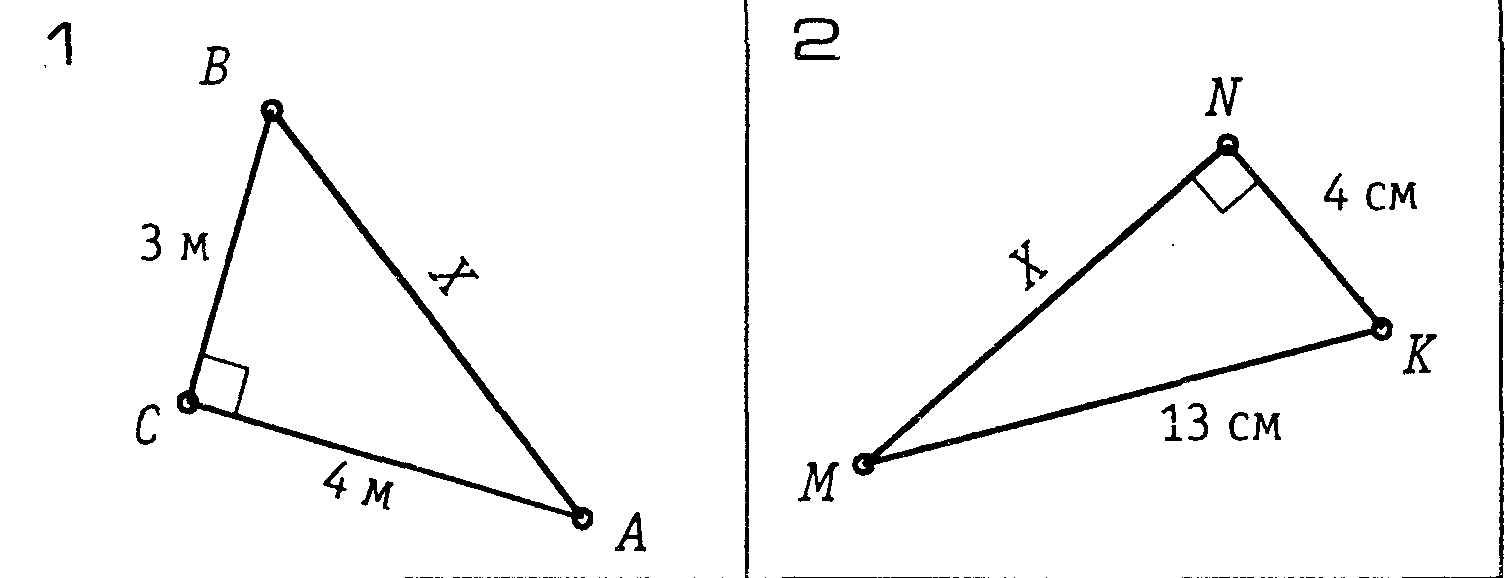
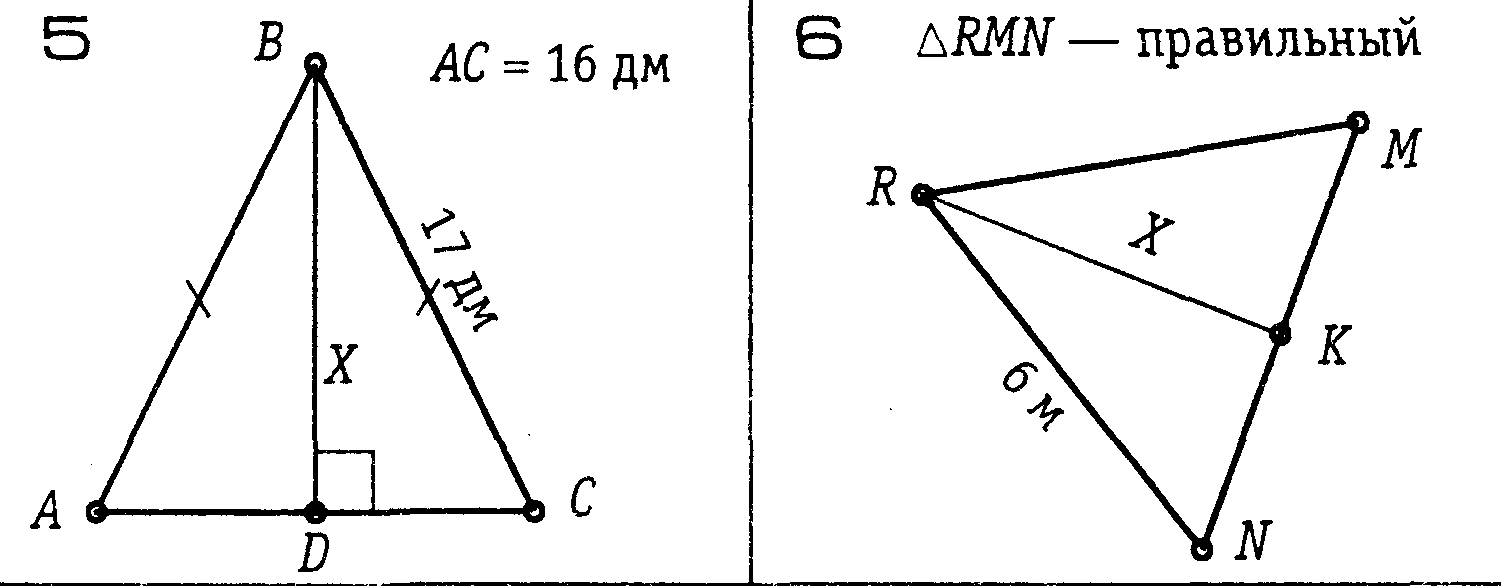
| Класс: 9 | Геометрия | Дата: | Урок: № 1 |
| Тема урока: Повторение изученного в 8 классе |
| Учитель: | Количество присутствующих: | Количество отсутствующих: |
| Цели обучения урока в рамках учебной программы по предмету | Закрепление знаний и умений по нахождению неизвестных элементов геометрических фигур с помощью их свойств и теоремы Пифагора. Развитие умения анализировать, синтезировать. Оценивать себя и других. Умение работать в команде. |
| Цели урока | Все учащиеся будут уметь: определять вид параллелограмма, трапеции и треугольника, знать их свойства Большинство учащихся будут уметь: определять вид параллелограмма, знать их свойства, составлять кластеры и таблицы свойств фигур, находить неизвестные элементы фигур Некоторые учащихся будут уметь: определять вид параллелограмма, знать их свойства, составлять кластеры и таблицы свойств фигур, находить неизвестные элементы фигур и их площади |
| Предыдущее обучение | Учащиеся умеют: Знают названия плоских фигур, их свойства, умеют применять теорему Пифагора, знают формулы площадей фигур |
| Дифференциация | Оценивание | Межпредметные связи |
| Дифференцируем задания | Взаимооценивание, самооценивание, критериальное оценивание | Развитие функциональной грамотности Алгебра |
| Ключевые слова: | Предметная лексика и терминология по теме: параллелограмм, ромб, квадрат, прямоугольник, трапеция, треугольник, высота, медиана, биссектриса, диагонали |
| ПЛАН урока |
| Вид деятельности | Деятельность учителя | Деятельность учащихся |
| Начало 3 мин
| Учитель приветствует учеников. Создает доброжелательную комфортную атмосферу. Стратегия «Круг радости». Послание добрых пожеланий друг другу. Учитель делит учеников на группы по фигурам: «Ромб, квадрат, треугольник, прямоугольник, трапеция, параллелограмм».
| Встают в круг и по очереди говорят комплименты, передавая друг другу солнышко. Учащиеся получают карточки с названиями фигур. Ученики, разработавшие правила, набирают в свои группы учащихся по фигурам. Находят членов своей группы. Ученики садятся на свои места. Оценивают свое эмоциональное состояние. Отмечают смайлики в карте оценивания.
|
| 2. Введение 4 мин
13 мин
5 мин
12 мин
| Задание №1 Учитель задает наводящие вопросы, для того, чтобы вывести цель урока нескольким ученикам. Учитель организовывает фронтальную беседу о геометрических фигурах и их свойствах.
Учитель предлагает сформулировать правила работы в группах. Учитель выбирает ученика, которому предлагает презентовать свою работу в группе.
Задание №2. Учитель организовывает работу для повторения учебного материала с помощью теста
Учитель предлагает оценить проделанную работу в группах с помощью стратегии «Светофор».
Задание №3.
Учитель предлагает приступить к выполнению следующего задания по ИАД и составлению решения задачи в тетради. Координирует работу групп (Приложение 2)
|
Ученики отвечают на вопросы учителя: Какие геометрические фигуры вы знаете? Какими свойствами они обладают? Какие существуют формулы для вычисления площади данной фигуры? Как вы думаете, какая сегодня тема урока?
Ученики отвечают на вопросы, затем работают с кластерами, в которых они должны изобразить геометрическую фигуру и указать необходимые свойства и формулы. Можно привести простейшие примеры. Спикер из одной группы зачитывает свои результаты. Выполняют самооценку своей работы. Стратегия «Большой палец». Если согласен полностью с ответом - палец вверх, не совсем согласен - палец в сторону, не согласен – палец вниз.
Ученики отвечают на вопросы теста (Приложение 1) |
| 1 | 2 | 3 | 4 | 5 | 6 | | 1 вар | 3 | 1 | 2 | 3 | 1 | 3 | | 2 вар | 3 | 3 | 1 | 2 | 1 | 2 | Красный – плохо 1-3 Желтый – хорошо -4-5 Зеленый – отлично -6
 
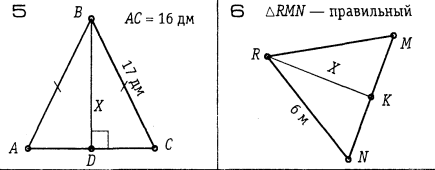
5 м 4. 3 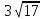 см 5. 15 дм см 5. 15 дм
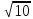 6. 6. 
Ученики меняются тетрадями, оценивают свои работы в парах по готовому образцу. Выставляют оценки в карту оценивания. 6 правильно – «5» 4-5 правильно – «4» 3 правильно – «3» 0-2 – плохо |
| 5. Рефлексия 6 мин | Учитель подводит итоги урока и предлагает оценить свою работу на уроке. Прием «Корзина» идей, понятий, терминов
Стратегия «Дерево успеха»
Стратегия «Облако тегов» |
Ученики пишут на листе с корзиной все термины, которые встречались на уроке. У кого полнее корзина?
На листе бумаги изображено дерево. Ученики прикрепляют свои листочки соответствующего цвета: зеленый – ответил правильно, желтый – есть небольшие затруднения, красный – много ошибок
Ученики выбирают по 1-2 высказывания и завершают их: Сегодня я узнал… Было трудно… Я понял, что… Я научился… Я смог… Было интересно узнать, что… Меня удивило… Меня удивило… |
| Домашнее задание 1 мин | Учитель предлагает домашнее задание Ученики записывают домашнее задание в дневник: Ш., ответить на вопросы, с.3.
|
| Итоговая оценка 1 мин | Учитель выставляет оценки в дневники учащимся |
| Тест. 1 вариант | Тест. 2 вариант |
| Ф. И. | Ф. И. |
Диагонали параллелограмма Являются биссектрисами его углов Равны В точке пересечения делятся пополам | Диагонали параллелограмма Равны Перпендикулярны В точке пересечения делятся пополам |
Биссектриса угла параллелограмма отсекает от него Равнобедренный треугольник Равносторонний треугольник Прямоугольный треугольник | Биссектрисы соседних углов параллелограмма образуют угол 30° 60° 90°
|
В ромбе Все углы равны Все стороны равны Диагонали равны | В ромбе Все высоты равны Все углы равны Диагонали равны |
Если в четырехугольнике противоположные стороны попарно равны, то он не может быть Прямоугольником Ромбом Трапецией | Если в четырехугольнике диагонали точкой пересечения делятся пополам, то он не может быть Прямоугольником Трапецией Ромбом |
Квадратом называется Ромб с равными диагоналями Прямоугольник с равными диагоналями Параллелограмм с равными диагоналями | Если в параллелограмме диагонали равны, то он не может быть Ромбом Квадратом Прямоугольником |
Если в параллелограмме диагонали перпендикулярны, то он не может быть Ромбом Квадратом Прямоугольником | Квадратом называется прямоугольник с равными диагоналями ромб с равными диагоналями параллелограмм с равными диагоналями |



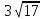 см 5. 15 дм
см 5. 15 дм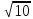 6.
6.