| I. Оргмомент, постановка целей урока.
|
| Учитель знакомит учащихся с темой целями и задачами урока. Сегодня на занятии мы с вами не раз будем цитировать слова великого математика, поэта, философа Омара Хайяма. Он призывает быть хозяевами своей судьбы. «Ты скажешь, эта жизнь – одно мгновенье. Её цени, в ней черпай вдохновенье. Как проведёшь её, так и пройдёт. Не забывай: она – твоё творенье». | Записывают в тетрадях число, тему урока. Формулируют задачи на урок, | 3 мин. |
| II.Актуализация знаний | 1. Игровой момент перед занятием: разгадывание двух кроссвордов “Тела и фигуры вращения” по группам. 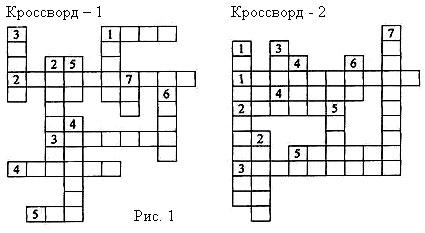
Вопросы к кроссворду – 1 По горизонтали. 1. Фигура на плоскости, все точки которой расположены не далее данного расстояния от одной точки. 2. Прямая, при вращении которой вокруг оси образуется боковая поверхность цилиндра, конуса. 3. Тело, полученное вращением прямоугольника вокруг одной из его сторон. 4. Угол между высотой и плоскостью основания конуса. 5. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его. По вертикали. 1. Тело, полученное вращением прямоугольного треугольника вокруг одного из его катетов. 2. Плоская фигура, при вращении которой образуется усечённый конус. 3. Тело вращения, являющееся верхней частью архитектурного сооружения. 4. Отрезок, соединяющий две точки сферы и проходящий через центр шара. 5. Тело, полученное вращением полукруга вокруг его диаметра. 6. Фигура, полученная вращением полуокружности вокруг её диаметра. 7. Тело вращения, об устойчивости движения которого написана известная работа великой русской женщины – математика. Вопросы к кроссворду – 2 По горизонтали. 1. Фигура, полученная вращением параболы вокруг её оси. 2. Отрезок, соединяющий центр сферы с любой её точкой. 3. Круг, являющийся элементом конуса, плоскость которого перпендикулярна оси конуса. 4. Музыкальный инструмент, часть которого напоминает Псевдосферу Лобачевского. 5. Отрезок, соединяющий две точки окружности. По вертикали. 1. Фигура, полученная вращением гиперболы вокруг её оси. 2. Перпендикуляр, опущенный из вершины конуса на плоскость основания. 3. Тело, полученное вращением круга вокруг оси, лежащей в плоскости круга и не пересекающей его. 4. Тело, полученное вращением полукруга вокруг его диаметра. 5. Фигура, полученная вращением полуокружности вокруг её диаметра. 6. Тело вращения, принцип движения которого описала великая русская женщина-математик. 7. Фигура, полученная вращением эллипса вокруг её оси. Ответы к кроссворду - 1. По горизонтали. 1. Круг. 2. Образующая. 3. Цилиндр. 4. Прямой. 5. тор. По вертикали. 1. Конус. 2. Трапеция. 3. Купол. 4. Диаметр. 5. Шар. 6. Сфера. 7. Юла. Ответы к кроссворду - 2. По горизонтали. 1. Параболоид. 2. Радиус. 3. Основание. 4. Труба. 5. Хорда. По вертикали. 1. Гиперболоид. 2. Высота. 3. Тор. 4. Шар. 5. Сфера. 6. Юла. 7. Эллипсоид. | На все ли вопросы вы ответили? Завершим разгадывание кроссворда в конце нашего занятия, используя новые знания.
| Обучающиеся отгадывают кроссворды, вписывают те ответы, которые знают. |
|
| III. Повторение теории по теме: «Цилиндр и конус. Площадь боковой и полной поверхности цилиндра и конуса»
| | 1 | Тело, ограниченное конической поверхностью и кругом с границей L, называется | R | конусом | | 2 | Боковой поверхностью цилиндра называется | A | цилиндрическая поверхность | | 3 | Осевым сечение конуса является | F | равнобедренный треу | | 4ольник
| Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L и L , называется , называется | T | цилиндром | | 5 | Осевым сечением цилиндра называется | S | сечение, содержащее ось цилиндра | | 6 | Боковой поверхн | стью называется конуса C | коническая поверхность | | 7 | Осевым сечение цилиндра является | V | прямоугольник | | 8 | Сечением цилиндра, плоскостью перпендикулярной оси цилиндра, является | B | прямоугольник | | 9 | Площадь полной поверхности конуса равна | E | S=  r(l+r) r(l+r) | | 10 | Площадь боковой поверхности цилиндра Равна | O | S= 2 rh rh | | 11 | За площадь боковой поверхности конуса принимается | P | площадь развертки конуса | | 12 | Площадь полной поверхности цилиндра равна | Y | S= 2 | | 13(r+h)
| За площадь боковой поверхности цилиндра принимается | H | площадь развертки цилиндра | | 14 | Площадь боковой поверхности цилиндра равна | L | S=  rl rl |
| Настраивает учащихся на выполнения работы. Работа по группам. Класс делится на 3 групп. | Выполняют задания. Учитель проверяет, выполненные задания, указывает ошибки. | 10 мин. |
| IV. Практическое значение математики | Обзор “Математика и история” (полная информация – на плакате).
Сообщение о проекции Г. Меркатора, о его атласе. Поверхность шара и карта мира Загадка карты Меркатора. Он никогда не совершал морских путешествий, все открытия сделал в своем кабинете, но его труды достойно венчают эпоху Великих географических открытий. Он собрал воедино все накопленные в Европе географические знания, создал наиболее точные карты. С Герарда Меркатора берет свое начало наука, получившая название картографии.
Эта удивительная карта была нарисована в 1538 году Герхардом Меркатором – чрезвычайно уважаемым картографом, жившим в 16 веке. Его работы весьма знамениты, и вы до сих пор можете купить атлас Меркатора в магазине. Он первым использовал слово «Атлас» для коллекции карт. И его работы в географии были столь же важны для развития науки, как и Коперника в астрономии. Кстати, он дружил и сотрудничал с известным алхимиком, магом и астрологом Джоном Ди. Был хорошим знатоком математики и в свое время даже преподавал ее. Разработал способ массового производства глобусов. Показать рисунок и модель “Седла” (пример криволинейной поверхности), рисунок Псевдосферы Лобачевского.
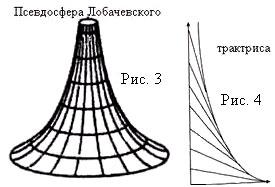
Псевдосфера Лобачевского – пример поверхности постоянной отрицательной кривизны, фигура вращения трактрисы вокруг оси. Геометрически трактриса характеризуется тем, что отрезок касательной к ней, заключённый между точкой касания и осью ординат, сохраняет постоянную длину/
Работа с плакатом “Тела и фигуры вращения”, с моделями (цилиндр, конус, усечённый конус, шар). 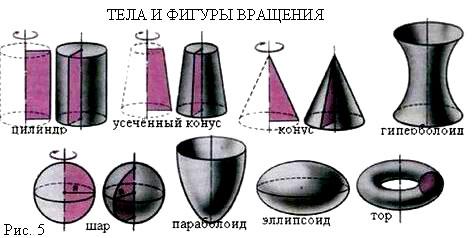
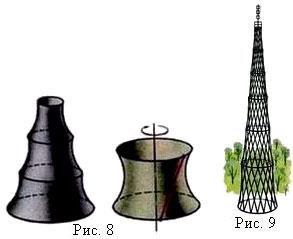
Сообщение о башне для радиостанции в Москве на Шаболовке, построенной по проекту замечательного русского инженера, почётного академика В. Г. Шухова. Она состоит из частей - гиперболоидов вращения. Причём, каждый из них изготовлен из прямолинейных металлических стержней, соединяющих соседние окружности.
О какой фигуре вращения говорится в загадке Один мы есть предпочитаем,
Другим – мы талию спасаем,
Третьим же мышцы подкачаем.
Четвёртым – транспорт подкуём,
И пятый – на воду бросаем.
А их геометрическую форму
Одним лишь, словом называем
Что это за слово? Ответ: это тор. Ещё вопрос: Предмет имеет два названья,
Он близок вам, почти родной.
И вместе с ним пришло признанье
Прекрасной женщине одной. Устойчивость его движенья
Хорошо все с детства знают.
Но та нашла ей объясненье,
Чьё имя мудрость означает. - О чём идёт речь? Ответ: юла или волчок.
Купол – тело вращения “Луковичная” форма купола – не случайна, она напоминает горящую свечу.
Конечно, такая форма купола практична. Но красота и духовность в сочетании с целесообразностью рождают гармонию. | Учитель показывает Таблицу 1 «Период элементарной математики» (времена, события - имена, открытия) Таблица 2 «Создание математики переменных величин». Таблица 3 «Современная математика» Знания о сфере пришли из астрономии. Омар Хайям писал: От земной глубины до далёких планет Мирозданья загадкам нашёл я ответ. От зенита Сатурна до чрева Земли Тайны мира своё толкованье нашли. 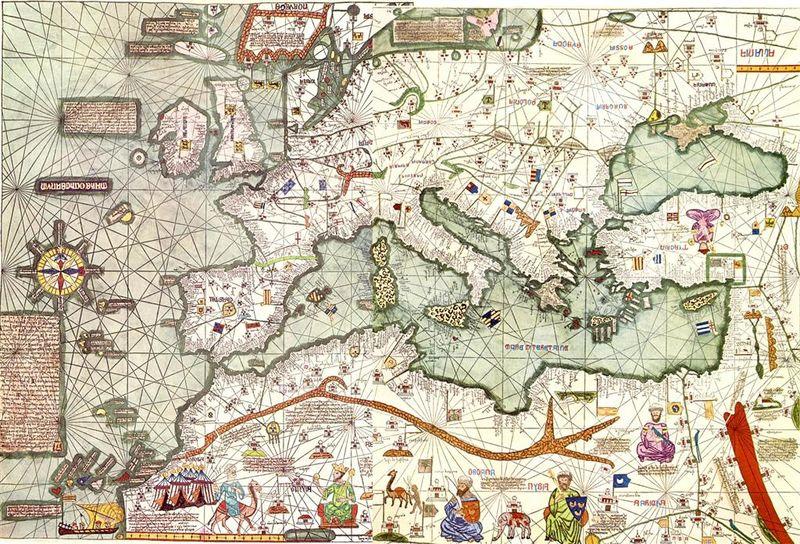
На уроках геометрии в школе мы изучаем прямолинейные поверхности, но в геометрии существуют и криволинейные поверхности. Познакомимся с некоторыми из них. 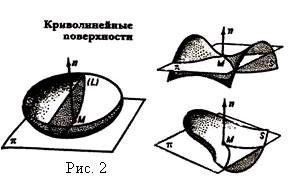
Загадывает загадку Есть, предпочитаем бублик, спасаем талию обручем, мышцы подкачаем резиновым эспандером, транспорт подкуём камерами колёс, на воду бросаем спасательный круг. Это – тело вращения (показать игрушку и рис. 10). 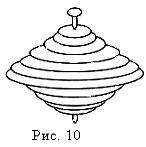 Великая русская женщина-математик Софья Ковалевская решила вопрос “О движении твёрдого тела вокруг неподвижной точки”. Речь шла о гироскопе, устроенном по принципу детского волчка, способного сохранять устойчивость движения.  В русском церковном искусстве проявилось стремление эстетику
чувств сочетать с эстетикой чисел, красоту свободно льющегося ритма
с красотой правильного геометрического тела. М. В. Алпатов | Ученики слушают, делают дополнения
Выполняют задание устно |
|
| VII. Подведение итогов занятия. Домашнее задание | Доработать задания кроссворда.
Решить задачу. «….Читал я где – то, Что царь однажды воинам своим Велел снести земли по горсти в кучу, И гордый холм возвысился, -и царь Мог с вышины с весельем озирать И дол, покрытый белыми шатрами, И море, где бежали корабли.» (А.С. Пушкин «Скупой рыцарь») 1. Предположив, что численность войска составляет 100 000 человек, объем горсти равен 0,2дм3,а угол при основании холма 450, найдите объем и высоту конуса.
|  | Учащиеся сравнивают свои знания в начале и конце урока |
|








 ано:
ано: