Соотношения между сторонами и углами прямоугольного треугольника

Этапы урока

Задачи этапа

Деятельность учителя

Деятельность учащихся

УУД

1. Организационный момент

Создать благоприятный психологический настрой на работу

Приветствие, проверка подготовленности к учебному занятию, организация внимания детей.

Включаются в деловой ритм урока.

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2.Целеполагание и мотивация

Обеспечение мотивации учения детьми, принятие ими целей урока.

Учебная ситуация: Предлагает учащимся 4 задачи.

Формулируют тему и цель и примерный план урока

Регулятивные: целеполагание.

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические – формулирование проблемы.

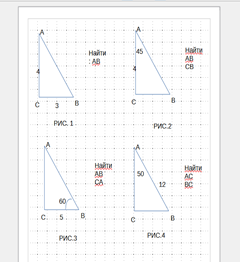
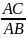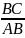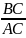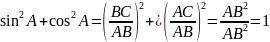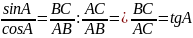3. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.

Актуализация опорных знаний и способов действий.

Задача 4 Посмотрим, позволят ли наши знания найти катет АС, если известна гипотенуза и острый угол В. Поможет ли нам в этом теорема Пифагора? (Нет)

Почему? (Нам известна только гипотенуза)

Сумма острых углов? (Нет)

Почему? (Не найдём сторону)

Есть ли у нас острый угол в 30 градусов? (Нет)

Осталось ли что-нибудь, что может связать гипотенузу, катет и острый угол? (Нет)

А оказывается, с прямоугольными треугольниками связаны интересные соотношения, которые могут это сделать. Только вы их пока не знаете. Давайте познакомимся с ними.

Запишите в тетрадях число, сегодня «29 января », «Классная работа» и тему сегодняшнего урока: «Соотношения между сторонами и углами прямоугольного треугольника».

Отвечают на поставленные вопросы

Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.

Познавательные: логические- анализ объектов с целью выделения признаков.

4. Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы: площади прямоугольника

Ещё во 2 веке до нашей эры древние математики заметили интересное свойство прямоугольного треугольника. Возьмём несколько прямоугольных треугольников с разными длинами сторон, но одним и тем же острым углом. Например, углом А. Каждый ряд считает свой треугольник.

Слайд 2.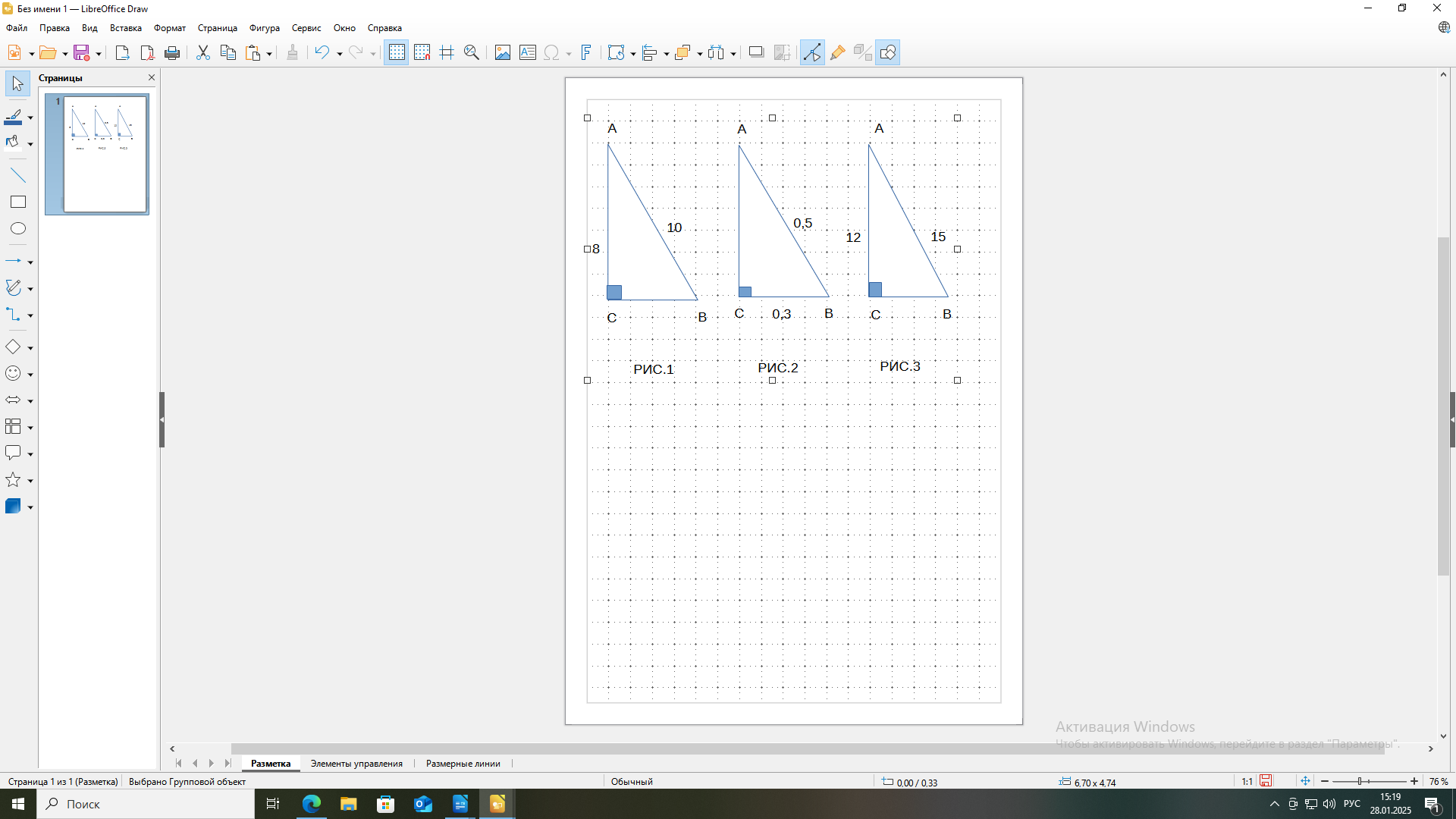

Чему равно отношение противолежащего катета к гипотенузе? (0,6)Отношение прилежащего катета к гипотенузе? (0,8)

Отношение противолежащего катета к прилежащему? (0,75)

Какая же закономерность очевидна? (Одинаковые ответы)

Верно, вы работали с разными числами, но получили одинаковые результаты, и эти результаты уже на протяжении сотен лет называют специальными терминами.

Отношение противолежащего катета к гипотенузе получило название «синуса угла».

Отношение прилежащего катета к гипотенузе – «косинуса угла».

Отношение противолежащего катета к прилежащему – «тангенсом угла».

Так что же мы будем называть синусом острого угла? (Отношение противолежащего катета к гипотенузе)

Косинусом острого угла? (Отношение прилежащего катета к гипотенузе)

Тангенсом острого угла? (Отношение противолежащего катета к прилежащему)

С помощью этих соотношений в дальнейшем будут заданы тригонометрических функций, которые вы очень подробно изучите на уроках алгебры в старших классах, а пока что вам достаточно знать, что слово «тригонометрия» переводится как «измерение треугольников», а синус, косинус и тангенс обозначаются следующим образом: «sin», «cos», «tg» и для острого угла A в прямоугольном треугольнике записываются в виде формул. Запишем их в тетрадь.

Впервые зависимости между сторонами и углами прямоугольного треугольника, были найдены древнегреческим астрономом Гиппархом во 2 веке до н.э.

В 4 веке появился уже специальный термин в трудах по астрономии индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Поскольку вычисления синуса тогда были связаны с полухордами в окружности, очень похожими на тетиву натянутого лука, то Ариабхата так и назвал это отношение «полутетива» или «ардхаджива» на санскрите. Затем термин сократился до просто «джива».

В 9 веке арабские учёные при переводе трудов Ариабхаты не стали оставлять буквальный смысл этого слова, а заменили созвучным арабским «джайб» - «впадина», тем самым потеряв первоначальное значение термина.

Европейские же учёные добросовестно перевели «впадину» на латынь, получив слово «синус», которым мы и пользуемся до сих пор.

История возникновения термина «косинус» не так интересна – это просто «дополнительный синус».

«Тангенс» был известен ещё в 10 веке учёным Востока, а в Европе его открыли заново только в 14 веке, а в 16 он получил современное звучание, которое означает «касающийся», что так же связано с окружностью.

Современные короткие обозначения были введены в 17 веке.

Отвечают на поставленные вопросы, пользуясь изученным материалом,

вычисляют в уме

Записывают результаты десятичной дробью.

Формулируют новые понятия, записывают их в тетрадь

cosA=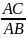

sinA=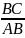

tgB=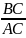

Коммуникативные: постановка вопросов, инициативное сотрудничество.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.

Регулятивные: планирование, прогнозирование.

5.Первичное закрепление и контроль

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

Решение задачи, определивших мотивацию к уроку

Ещё древними учёными были найдены соотношения, связывающие синус, косинус и тангенс друг с другом простыми формулами. И вам сейчас предстоит получить одну из них. Обсудите в течении минуты в группах, как найти:

1.Сумму квадратов синуса и косинуса угла А, используя определения синуса и косинуса и другие ваши знания из математики, показанные на слайде.

2. Отношение синуса угла А к косинусу угла А.

Давайте обсудим, к какому результату вы пришли.

Как записать синус угла А? Косинус угла А?

Как возвести обыкновенную дробь в квадрат? (Возвести числитель и возвести знаменатель

Что можно сделать дальше? (Сложить числители)

Дальше? (В числителе по теореме Пифагора получилась гипотенуза в квадрате)

Что осталось сделать? (Сократить)

Что получается? (Единица)

Как вы думаете, получили бы вы единицу, если работали не с углом А, а с углом В? (Да)

Выпишем начало и конец преобразования. Какое правило можно сформулировать по этой формуле? (Сумма квадратов синуса и косинуса одного и того же угла равна единице)

Данная формула получили название основного тригонометрического тождества.

2. Что запишем вместо синуса угла А?

Что вместо косинуса угла А?

Что получим в результате деления?

Это отношение равно тангенсу угла А.

Кроме него есть ещё много других тригонометрических тождеств, которые используются при расчётах в различных областях современной науки от спутниковой навигации до экономики. Вы их будете изучать в старших классах на уроках алгебры. С их помощью, зная синус, можно найти косинус и тангенс и наоборот. Этому вы научитесь уже на следующем уроке.

Последним шагом к достижению цели нашего урока станет ответ на вопрос – а можно ли найти значение синуса, косинуса и тангенса, зная только градусную меру угла?

Ответ прост – можно, и это можно было сделать ещё более двух тысяч лет назад, во времена греческого астронома Гиппарха, который первым составил таблицы значений синуса, косинуса и тангенса. Сегодня все эти значения собраны в специальном сборнике Владимира Модестовича Брадиса «Четырёхзначные математические таблицы», пользоваться которыми мы научимся на уроках математики, хотя в этом можно разобраться и самостоятельно, а потом приятно удивить учителя.

Слайд 1 Вспомним, какую цель мы поставили перед собой в начале урока? (Найти стороны треугольника)

Итак, нам известны гипотенуза и острый угол В в прямоугольном треугольнике, а так же определения синуса, косинуса и тангенса острого угла. Поможет ли какое-нибудь из новых определений решить нашу проблему? (Синус)

Почему именно синус? (Он связывает вместе гипотенузу, угол и искомый катет)

Как? (Гипотенузу умножим на синус 50 градусов)

Значение синуса возьмём из таблицы.

Вам остаётся только выполнить умножение (9,192)

Округлим ответ до целых (9 м)

Как найти ВС?( Гипотенузу умножить на косинус 50 градусов)

Что позволило нам решить проблему? (Синус и косинус)

Что такое синус? (Отношение противолежащего катета к гипотенузе)

Что такое косинус? (Отношение прилежащего катета к гипотенузе)

Производят расчеты.

Выводят формулы

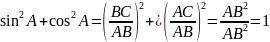
основное тригонометрическое тождество

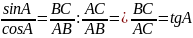
Отвечают на вопросы, опираясь на знания

Планируют дальнейшие действия, опираясь на ранее изученный материал.

Знакомятся с четырехзначными таблицами и смотрят как ими можно пользоваться

Вычисляют стороны треугольника, достигая цели урока

АС=12*sin50=12*0?766=9,192=9

ВС=12*COS50=12*0,6428=7,7136=8

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.

6.Динамическая пауза

Зрительная гимнастика

Смена вида деятельности

Так как мы с вами уже долгое время работаем, то нашим глазам необходим отдых, Вы согласны? Давайте выпрямим свои спинки, закроем глаза, повернем голову направо, а затем налево и представим с вами картинку, что сейчас лето, прекрасная погода, у вас отличное настроение, и вы полны к дальнейшим свершениям. Откройте глаза, как ваше самочувствие, готовы работать дальше? Тогда продолжим.

Выполняют релаксационные упражнения, расслабляются

Самоконтроль, осознание собственных ощущений, состояния

7. Подведение итогов урока.

Дать качественную оценку работы класса и отдельных обучаемых

-Что изучили сегодня на уроке?

-Кто желает сформулировать определение синуса?

-Кто желает сформулировать определение косинуса?

-Кто желает сформулировать определение тангенса?

Оценить отдельных учащихся

Самостоятельно, без помощи учителя формулируют новые понятия и проговаривают как можно решать подобные задачи

Регулятивные: оценка-осознание уровня и качества усвоения; контроль

8. Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

Давайте запишем домашнее задание.

Выучить определение синуса, косинуса и тангенса острого угла прямоугольного треугольника; выучить основное тригонометрическое тождество из учебника п. 74 и выполнить № 697, похожий на задания сегодняшнего урока.

Получают домашнее задание

9. Рефлексия

Учебная Инициировать рефлексию знаний детей ,

полученных на уроке Эмоциональная

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Что вы узнали на уроке нового?

Чему вы научились на уроке?

Понравилось ли вам на уроке

определяются что нового узнали, чему научились, и что благодаря этому можно делать

Коммуникативные:

умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.