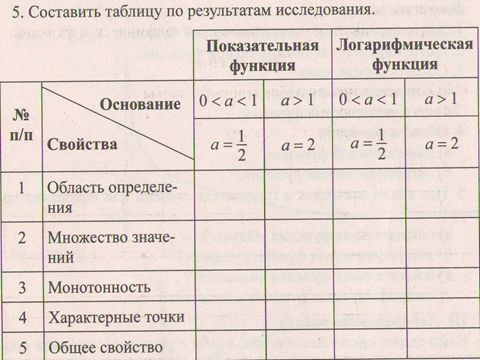
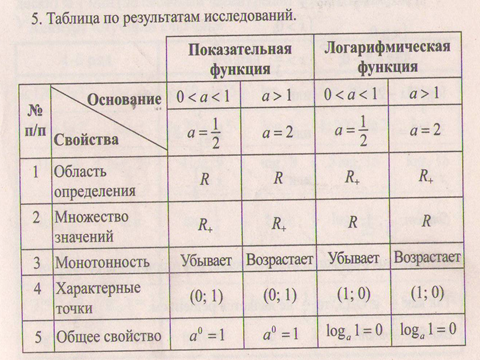
Данный урок позволяет организовать исследовательскую лабораторную работу, в результате которой устанавливаем взаимосвязь показательной и логарифмической функций и их свойств, выполняем построение графика функции, сводим результаты исследований в таблицу.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок по теме: «Показательная и логарифмическая функции, их свойства и графики»
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Урок по теме: «Показательная и логарифмическая функции, их свойства и графики»»
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
2200 руб.
3140 руб.
2440 руб.
3480 руб.
2560 руб.
3650 руб.
2220 руб.
3170 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
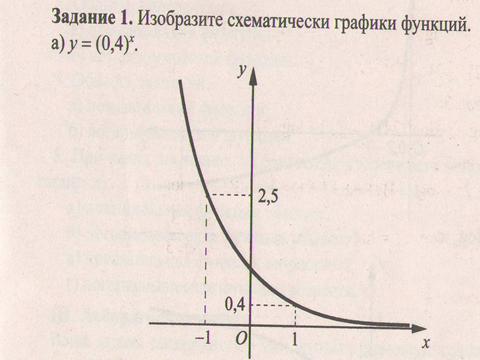
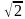 )х
)х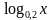
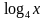
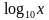
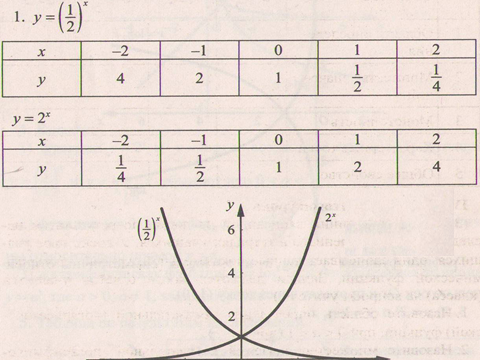
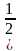 )х и у= 2х .Сделать вывод об области определения , множестве значений и монотонности функций у = ах в зависимости от а .
)х и у= 2х .Сделать вывод об области определения , множестве значений и монотонности функций у = ах в зависимости от а .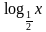 и у =
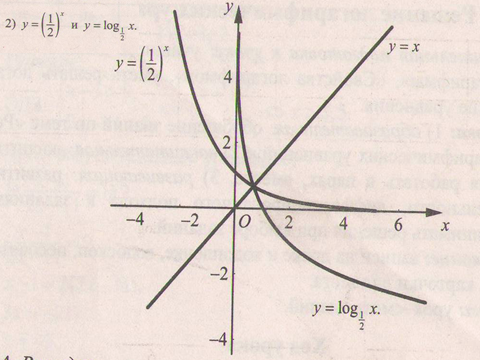
и у = 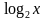 . Сделать вывод о симметричности графиков функций. Указать характерные точки.
. Сделать вывод о симметричности графиков функций. Указать характерные точки.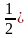 х и у =
х и у = 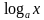 при 0
при 0 1 и при а
1 и при а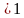 ;
; 0
0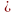 а
а 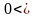 а
а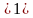 .
.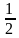 )х и у = 2х ;
)х и у = 2х ;