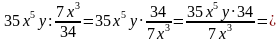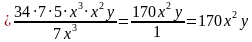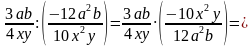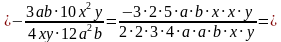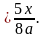Вы знаете, что при умножении обыкновенных дробей перемножают отдельно их числители и их знаменатели, первое произведение записывают в числителе, а второе – в знаменателе дроби.
Свойство 1. Равенство ab∙cd=ac/bd верно при любых значениях переменных, т.е. при b≠0 и d≠0.
Правило умножения рациональных дробей:
Чтобы умножить рациональную дробь на рациональную дробь, нужно перемножить числители и записать в числителе, перемножить знаменатели и записать в знаменатель.
Пример:
1) 92a∙5a3=9∙5a2a∙3=3∙3∙5∙a3∙2∙a=152=7,5 ;
2) b210∙5b=5∙b210∙b=5∙b∙b5∙2∙b=b2 ;
Свойство 1. Равенство ab∙cd=ac/bd верно при любых значениях переменных, т.е. при b≠0 и d≠0 .
Правило умножения рациональных дробей:
Чтобы умножить рациональную дробь на рациональную дробь, нужно перемножить числители и записать в числителе, перемножить знаменатели и записать в знаменатель.
Примеры:
1) 92a∙5a3=9∙5a2a∙3=3∙3∙5∙a3∙2∙a=152=7,5 ;
2) b210∙5b=5∙b210∙b=5∙b∙b5∙2∙b=b2 ;
Свойство 2. Равенство abn=anbn , n – целое число, верно при любых допустимых значениях переменных, т.е. при b≠0 .
Правило возведения рациональной дроби в степень:
Чтобы возвести рациональную дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй – в знаменателе дроби.
Пример: Возведем рациональную дробь 5m46n7 в квадрат.
5m46n72=5m426n72=25m836n14 ;
Свойство 3. Равенство a/b:c/d=a/b∙d/c верно при любых значениях переменных, т.е. при b≠0, c≠0 и d≠0 .
Правило деления рациональных дробей:
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
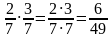
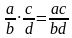верно при любых значениях переменных, т.е. при 
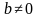и 
. 
;
;
, 
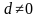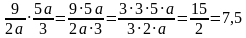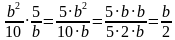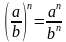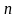– целое число, верно при любых допустимых значениях переменных, т.е. при 
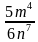в квадрат. 
; 
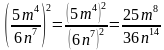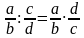верно при любых значениях переменных, т.е. пр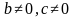и 
и 
