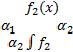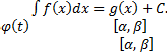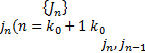| Сабақтың тақырыбы:Анықталғанинтеграл. Ньютон-Лейбницформуласы | Мектеп:№19 М.Мәметова ЖОМ | ||||
| Күні: 24.09.2017жыл | Мұғалімнің аты-жөні: Қолдасова Айсапар | ||||
| Сынып: 11 | Қатысқаноқушысаны: | Қатыспағаноқушысаны: | |||
| Осысабақтақолжеткізілетіноқумақсаттары | Оқушылар: осытақырыпбойыншабілу, түсіну, талдау, қолдану, анализ, синтезойлаудағдыларынқалыптастырады. | ||||
| Сабақтыңмақсаты | Тақырыпаясындаберілгенесептердішығараалады, яғнитеориялықалғанбілімінпрактикадақолданаалады. | ||||
| Жетістіккритерийлері | Оқушыларосытақырыпбойыншабілу, түсіну, талдау, қолдану, анализ, синтезойлаудағдыларынқалыптастыруытиіс. | ||||
| Тілдікмақсат | Осытақырыпқақатыстытерминдердіүштілдемеңгереді, қазақ, орыс, ағылшынтіліндегіәдебиеттердегіматериалдардымеңгереалады. Олүшінмынадайсөздіктерқолданамын. | ||||
| Құндылықтардыдамыту | Болашаққабағдар: Руханижаңғырудың 6 негізгібағыты - бәсекегеқабілеттілік, прагматизм, білімніңсалтанатқұруы, сананыңашықтығы, Туғанжербағдарламасы, латынәліпбиінекөшу, «100 жаңаоқулық» аясындапатриоттыққатәрбиелеу | ||||
| Пәнаралықбайланыс | Геометрия, тұрмыстақолданаалу | ||||
| АКТ қолданудағдылары | Интерактивтітақста, интернет ресурстары (сайттар, видеолар, есептер), таратпаматериалдар, көрнекі-демонстрациялыққұралдар, фигуралар | ||||
| Бастапқыбілім | |||||
| Сабақбарысы | |||||
| Сабақтыңкезеңдері | Сабақтаорындалатыніс-әрекеттер | Оқытуресурстары | |||
| Басы 5минут | ҰйымдастырусәтіҮйжұмысынтексеру Мат алықесептерберуарқылы«Миғашабуыл» АстанаданАлматығаұшақ 1 сағат 30 минутұшқан. Алкеріқайтқандабасқажолмен 90 минутұшқан. Қайжолтиімді? Жыл он екіайдыңішінде 30 және 31 сандарыауысыпотырады. Ал 28 саны қай айда кездеседі? | ||||
| Негізгібөлім | Рекуренттіформулалар. Интегралдаудыңжалпыәдістері: 1. Жіктеуәдісі; 2. Айнымалыныауыстыру | ||||
|
|