Тақырыбы:
Анықталған интеграл.
Ньютон-Лейбниц формуласы
Пәні: алгебра
Сабақ: № 16
Күні: 11.10
Пән мұғалімі: Аюбаева З.А
Сынып: 11б
Қатысқандар саны: 11
Қатыспағандар саны: -
Сабақ негізделген оқу мақсаты (мақсаттары)
Оқушылар алғашқы функцияның негізгі қасиетімен және алғашқы функцияны табудың ережелерін алғашқы функцияны және анықталған интегралды табуда пайдалануға дағдыланады.
Логикалық ойлау қабілеті мен есептеу дағдылары дамиды, өз бетінше еңбектенеді, белсенділіктерін арттырады, оқушылардың құзыреттерін қалыптастырады.
Оқушылар өз ойын толық, дұрыс жеткізе білуге, тапқырлыққа, жылдамдыққа, ептілікке, достық қарым-қатынасқа ұмтылады.
Сабақ мақсаттары:
Барлық оқушылар: алғашқы функцияның негізгі
қасиетімен және алғашқы функцияны табудың
ережелерін алғашқы функцияны және анықталған
интегралды табуда пайдаланады
Оқушылардың басым бөлігі: Ньютон-Лейбниц
формуласын пайдаланып анықталған интегралды
есептей алады
Кейбір оқушылар: алғашқы функцияның кестесін
есептер шығаруда қолдана алады
Алдыңғы оқу
Алғашқы функцияның негізгі қасиеті және алғашқы функцияны табудың ережелері, алғашқы функцияның кестесі, қисықсызықты трапецияның ауданы, анықталған интеграл


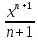 + С
+ С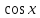 ; Ғ(х) =
; Ғ(х) = 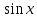 + С
+ С 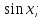 Ғ(х) = -
Ғ(х) = - 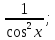 Ғ(х) = tgх + С
Ғ(х) = tgх + С 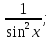 Ғ(х) = - ctgх + С
Ғ(х) = - ctgх + С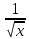 Ғ(х) = 2
Ғ(х) = 2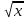 + С
+ С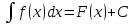
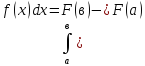
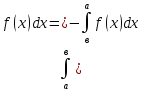

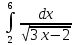
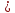
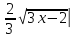 26
26 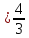
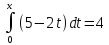 ; х = 1; х = 4
; х = 1; х = 4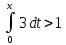 ; Ж: (
; Ж: (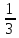 ; +
; +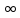 )
)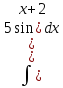
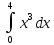
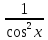
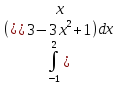
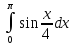
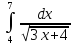
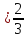
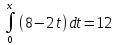 ; х = 2; х = 6
; х = 2; х = 6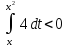 ; Ж: (0;1)
; Ж: (0;1)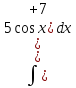
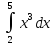
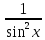
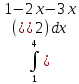
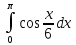


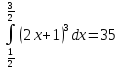
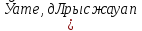 30)
30)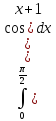
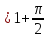 (дұрыс)
(дұрыс)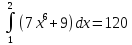
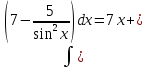 ctgx + C
ctgx + C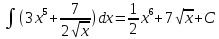 (дұрыс)
(дұрыс)
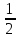 х(х – 1) = 78
х(х – 1) = 78 
















