Рабочая программа по алгебре в 7-9 классах на основе ФГОС ООО

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа № 32»

Копейского городского округа

Рассмотрено на заседании методического объединения протокол № __ от ____ 2017 г. Руководитель МО _________

Согласовано: Зам. директора по УВР Туманова Ю.Э. __________ «____» ___________ 2017 г.

Утверждаю: Директор МОУ «СОШ № 32» О.А. Тарасова __________ «____» ___________ 2017 г.

Туманова Ю.Э.

Рабочая программа

Учебный предмет	АЛГЕБРА
Предметная область	Математика и информатика
Класс	7-9
Учитель	Туманова Ю.Э.
Квалификационная категория	Высшая
Стаж	21 год
Количество часов в неделю по учебному плану		11 (4/4/3)
Количество часов по учебному плану в год		374 (136/136/102)

Копейск, 2017

Оглавление

I. Пояснительная записка 3

II. Планируемые результаты освоения учебного предмета «Алгебра» 10

III. Содержание учебного предмета «Алгебра» 13

VI. Тематическое планирование 15

V. Календарно-тематическое планирование 22

VI. Реализация национальных, региональных и этнокультурных особенностей 31

I. Пояснительная записка

Сведения о программе

Программа основного курса алгебры составлена в соответствии с требованиями федерального государственного образовательного стандарта второго поколения основного общего образования, с примерной программой по курсу алгебры (7 – 9 классы), созданной на основе единой концепции преподавания математики в средней школе, разработанной  А.Г.Мерзляком, В.Б.Полонским, М.С.Якиром, Д.А. Номировским, включенных в систему «Алгоримт успеха» (М.: Вентана-Граф, 2014) и обеспечена УМК для 7-9-го классов «Алгебра – 7», «Алгебра – 8» и «Алгебра – 9»/  А.Г.Мерзляк, В.Б.Полонский, М.С.Якир/М.: Вентана-Граф, 2014. и скорректирована на основе авторской программы по математике для УМК А.Г. Мерзляка и др. (Математика : рабочие программы : 5—11 классы / А. Г. Мерзляк, В. Б. Полонский, М. С. Якир, Е. В. Буцко. — 2-е изд., перераб. — М. : Вентана-Граф, 2017. — 164 с.).

Уровень обучения – базовый.

Нормативно-правовая база:

Федеральный уровень

1. Федеральный закон от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» (с изм., внесенными Федеральными законами от 04.06.2014 г. № 145-ФЗ, от 06.04.2015 г. № 68-ФЗ) // http://www.consultant.ru/; http://www.garant.ru/

2. Приказ Министерства образования и науки Российской Федерации от 31.03.2014 г. № 253 «Об утверждении Федерального перечня учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования» (в ред. Приказов Минобрнауки России от 08.06.2015 г. № 576, от 28.12.2015 г. № 1529, от 26.01.2016 г. № 38) // http://www.consultant.ru/; http://www.garant.ru/

3. Приказ Минтруда России от 18.10.2013 г. № 544н (с изм. от 25.12.2014 г.) «Об утверждении профессионального стандарта «Педагог (педагогическая деятельность в сфере дошкольного, начального общего, основного общего, среднего общего образования) (воспитатель, учитель)» (Зарегистрировано в Минюсте России 06.12.2013 г. № 30550) // http://www.consultant.ru/; http://www.garant.ru/

4. Приказ Министерства образования и науки Российской Федерации от 30.08.2013 г. № 1015 (ред. от 28.05.2014 г.) «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам – образовательным программам начального общего, основного общего и среднего общего образования» (Зарегистрировано в Минюсте России 01.10.2013 г. № 30067) // http://www.consultant.ru/; http://www.garant.ru/

5. Постановление Главного государственного санитарного врача Российской Федерации от 29.12.2010 № 189 (ред. от 25.12.2013 г.) «Об утверждении СанПиН 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (Зарегистрировано в Минюсте России 03.03.2011 г. № 19993), (в ред. изменений № 1, утв. Постановлением Главного государственного санитарного врача Российской Федерации от 29.06.2011 № 85, Изменений № 2, утв. Постановлением Главного государственного санитарного врача Российской Федерации от 25.12.2013 г. № 72, Изменений № 3, утв. Постановлением Главного государственного санитарного врача РФ от 24.11.2015 г. № 81) // http://www.consultant.ru/; http://www.garant.ru/

6. Постановление Главного государственного санитарного врача Российской Федерации от 10.07.2015 г. № 26 «Об утверждении СанПиН 2.4.2.3286-15 «Санитарно-эпидемиологические требования к условиям и организации обучения и воспитания в организациях, осуществляющих образовательную деятельность по адаптированным основным общеобразовательным программам для обучающихся с ограниченными возможностями здоровья» (Зарегистрировано в Минюсте России 14.08.2015 г. № 38528) // http://www.consultant.ru/; http://www.garant.ru/

7. Приказ Министерства образования и науки Российской Федерации от 09.06.2016 г. № 699 «Об утверждении перечня организаций, осуществляющих выпуск учебных пособий, которые допускаются к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования» (Зарегистрировано в Минюсте России 04.07.2016 г. № 42729) // // http://www.consultant.ru/

8. Приказ Министерства образования и науки Российской Федерации от 25.12.2013 г. № 1394 (ред. от 03.12.2015 г.) «Об утверждении Порядка проведения государственной итоговой аттестации по образовательным программам основного общего образования» (Зарегистрировано в Минюсте России 03.02.2014 г. № 31206) // http://www.consultant.ru/; http://www.garant.ru/

9. Приказ Министерства образования и науки Российской Федерации от 17.12.2010 г. № 1897 (в ред. Приказов Минобрнауки России от 29.12.2014 г. № 1644, от 31.12.2015 г. № 1577) «Об утверждении федерального государственного образовательного стандарта основного общего образования» (Зарегистрирован Минюстом России 01.02.2011 г. № 19644) // http://www.consultant.ru/; http://www.garant.ru/

10. Распоряжение Правительства Российской Федерации от 24.12.2013 г. № 2506-р «Об утверждении Концепции математического образования в Российской Федерации».

Региональный уровень

1. Закон Челябинской области от 29.08.2013 № 515-ЗО (ред. от 28.08.2014) «Об образовании в Челябинской области (подписан Губернатором Челябинской области 30.08.2013 г.) / Постановление Законодательного Собрания Челябинской области от 29.08.2013 г. № 1543.

2. Приказ Министерства образования и науки Челябинской области от 31.12.2014 г. № 01/3810 «Об утверждении Концепции развития естественно-математического и технологического образования в Челябинской области «ТЕМП»

Школьный уровень

1.Основная образовательная программа ООО МОУ «СОШ № 32» Копейского городского округа (приказ от  01.09.2016 г. №1, приказ от 01.09.2017 г. №1).

2. Адаптированная основная общеобразовательная программа ООО для обучающихся с ЗПР МОУ «СОШ № 32» (приказ от  01.09.2016 г. №1, приказ от 01.09.2017 г. №1).

3. Приказ МОУ «СОШ № 32» от 01.09.2017 г. № 6-ОД «Об организации специального (коррекционного) образования в школе в 2017-2018 учебном году». 

4.Положение о рабочих программах учебных предметов, курсов, дисциплин (модулей) МОУ «СОШ № 32» Копейского городского округа.

В данных документах учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основ­ного общего образования. Сознательное овладение учащимися системой алгебраиче­ских знаний и умений необходимо в повседневной жизни для изучения смежных дисциплин и продолжения образования.

Практическая значимость школьного курса алгебры обу­словлена тем, что её объектом являются количественные отно­шения действительного мира. Математическая подготовка не­обходима для понимания принципов устройства и использова­ния современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.

Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В пер­вую очередь это относится к предметам естественно – научного цикла, в частности к физике, информатике. Развитие логического мышления учащихся при обучении алгебре способствует усвоению пред­метов гуманитарного цикла. Практические умения и навыки алгебраического характера необходимы для трудовой и профес­сиональной подготовки школьников.

Развитие у учащихся правильных представлений о сущности и происхождении алгебраических абстракций, соотношении ре­ального и идеального, характере отражения математической на­укой явлений и процессов реального мира, месте алгебры в си­стеме наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся и качеств мышления, необходимых для адаптации в современном информационном обществе.

Требуя от учащихся умственных и волевых усилий, концен­трации внимания, активности развитого воображения, алгебра развивает нравственные черты личности (настойчивость, целе­устремленность, творческую активность, самостоятельность, от­ветственность, трудолюбие, дисциплину и критичность мышле­ния) и умение аргументировано отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.

Изучение алгебры, функций, вероятности и статистики су­щественно расширяет кругозор учащихся, знакомя их с индук­цией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагировани­ем, аналогией. Активное использование задач на всех этапах учебной деятельности развивает творческие способности школьни­ков.

Изучение алгебры позволяет формировать умения и навыки умственного труда — планирование своей работы, поиск раци­ональных путей её выполнения, критическая оценка результа­тов. В процессе изучения алгебры школьники должны научить­ся излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.

Важнейшей задачей школьного курса алгебры является раз­витие логического мышления учащихся. Сами объекты матема­тических умозаключений и принятые в алгебре правила их кон­струирования способствуют формированию умений обосновы­вать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрыва­ют механизм логических построений и учат их применению. Тем самым алгебра занимает одно из ведущих мест в формиро­вании научно-теоретического мышления школьников. Раскры­вая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вно­сит значительный вклад в эстетическое воспитание учащихся.

Курс алгебры 7 – 9 классов является базовым для математического образования и развития школьников. Алгебраические знания необходимы для изучения геометрии в 7 – 9 классах, алгебры и математического анализа в 10 – 11 классах, а также изучения смежных дисциплин. При этом учитываются доминирующие идеи и положения программы развития и формирования универсальных учебных действий для основного общего образования, которые обеспечивают формирование российской гражданской идентичности, коммуникативных качеств личности и способствуют формированию ключевой компетенции – умения учиться.

В основу настоящей программы положено Фундаментальное ядро содержания общего образования, требования к результатам освоения образовательной программы основного общего образования, представленные в федеральном государственном образовательном стандарте основного общего образования, с учётом преемственности с примерными программами для начального общего образования по математике.

Практическая значимость школьного курса алгебры 7– 9 классов состоит в том, что предметом его изучения являются количественные отношения и процессы реального мира, описанные математическими моделями. В современном обществе математическая подготовка необходима каждому человеку, так как математика присутствует во всех сферах человеческой деятельности.

Одной из основных целей изучения алгебры является развитие мышления. В процессе изучения алгебры формируется логическое и алгоритмическое мышление, а также такие качества мышления, как сила и гибкость, конструктивность и критичность. Для адаптации в современном информационном обществе важным фактором является формирование математического стиля мышления, включающего в себя индукцию и дедукцию, обобщение и конкретизацию, анализ и синтез, классификацию и систематизацию, абстрагирование и аналогию. Т

Обучение алгебре даёт возможность учащимся научиться планировать свою деятельность, критически оценивать её, принимать самостоятельные решения, отстаивать свои взгляды и убеждения. Учащиеся, в процессе изучения алгебры, учатся излагать свои мысли ясно и исчерпывающе, приобретают навыки чёткого и грамотного выполнения математических записей, при этом использование математического языка позволяет развивать у школьников грамотную устную и письменную речь.

Формирует у учащихся представление об алгебре как части общечеловеческой культуры и знакомство с историей развития алгебры как науки. Значительное внимание в изложении теоретического материала курса уделяется его мотивации, раскрытию сути основных понятий, идей, методов. Обучение построено на базе теории развивающего обучения, что достигается особенностями изложения теоретического материала и упражнениями на сравнение, анализ, выделение главного, установление связей, классификацию, обобщение и систематизацию. Особо акцентируются содержательное раскрытие математических понятий, толкование сущности математических методов и области их применения демонстрация возможностей применения теоретических знаний для решения разнообразных задач прикладного характера, например решения текстовых задач, денежных и процентных расчетов, умение пользоваться количественной информацией, представленной в различных формах, умение читать графики. Осознание общего, существенного является основной базой для решения упражнений. Важно приводить детальные пояснения к решению типовых упражнений. Этим раскрывается суть метода, подхода, предлагается алгоритм или эвристическая схема решения упражнений определенного типа.

В основу настоящей программы положены педагогические и дидактические принципы вариативного развивающего образования, изложенные в концепции образовательной программы «Перспективная школа», и современные дидактико-психологические тенденции, связанные с вариативным развивающим образованием и требованиями ФГОС.

А. Личностно ориентированные принципы: принцип адаптивности; принцип развития; принцип комфортности процесса обучения.

Б. Культурно ориентированные принципы: принцип целостной картины мира; принцип целостности содержания образования; принцип систематичности; принцип смыслового отношения к миру; принцип ориентировочной функции знаний; принцип опоры на культуру как мировоззрение и как культурный стереотип.

В. Деятельностно ориентированные принципы: принцип обучения деятельности; принцип управляемого перехода от деятельности в учебной ситуации к деятельности в жизненной ситуации; принцип перехода от совместной учебно-познавательной деятельности к самостоятельной деятельности учащегося (зона ближайшего развития); принцип опоры на процессы спонтанного развития; принцип формирования потребности в творчестве и умений творчества.

Математическое образование является обязательной и не­отъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих целей:

1) в направлении личностного развития:

• Формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• Развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• Формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• Формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• Развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении:

• Развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

3) в предметном направлении:

• Овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;

• Создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

В организации образовательной деятельности важную роль играют задачи. Они являются и целью, и средством обучения. Важным условием правильной организации этого процесса является выбор рациональной системы методов и приемов обучения, специфики решаемых образовательных и воспитательных задач.

Целью изучения курса математике в 7 - 9 классах является развитие вычислительных умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования задач, осуществление функциональной подготовки школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилием роли теоретических обобщений и дедуктивных заключений. Прикладная направленность раскрывает возможность изучать и решать практические задачи.

В основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям.

Предлагаемый курс позволяет обеспечить формирование как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач.

В курсе алгебры можно выделить следующие основные со­держательные линии: арифметика; алгебра; функции; вероят­ность и статистика. Наряду с этим в содержание включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализаци­ей целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачива­ется в содержательно-методическую линию, пронизывающую все основные содержательные линии. При этом первая ли­ния — «Логика и множества» — служит цели овладения учащи­мися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — спо­собствует созданию общекультурного, гуманитарного фона из­учения курса.

Общая характеристика учебного предмета

Настоящая программа по математике для основной школы является логическим продолжением программы «Перспективная школа» для начальной школы, а также продолжением курса «Математика» 5 – 6 класса и вместе с ней составляет описание непрерывного курса математики с 1-го по 9-й класс общеобразовательной школы по ФГОС.

В основе содержания обучения математике лежит овладение учащимися следующими видами компетенций: предметной, коммуникативной, организационной и общекультурной. В соответствии с этими видами компетенций выделены главные содержательно-целевые направления развития учащихся средствами предмета «Математика».

Предметная компетенция. Под предметной компетенцией понимается осведомлённость школьников о системе основных математических представлений и овладение ими необходимыми предметными умениями. Формируются следующие образующие эту компетенцию представления: о математическом языке как средстве выражения математических законов, закономерностей и т.д.; о математическом моделировании как одном из важных методов познания мира. Формируются следующие образующие эту компетенцию умения: создавать простейшие математические модели, работать с ними и интерпретировать полученные результаты; приобретать и систематизировать знания о способах решения математических задач, а также применять эти знания и умения для решения многих жизненных задач.

Коммуникативная компетенция. Под коммуникативной компетенцией понимается сформированность умения ясно и чётко излагать свои мысли, строить аргументированные рассуждения, вести диалог, воспринимая точку зрения собеседника и в то же время подвергая её критическому анализу, отстаивать (при необходимости) свою точку зрения, выстраивая систему аргументации. Формируются образующие эту компетенцию умения, а также умения извлекать информацию из разного рода источников, преобразовывая её при необходимости в другие формы (тексты, таблицы, схемы и т.д.).

Организационная компетенция. Под организационной компетенцией понимается сформированность умения самостоятельно находить и присваивать необходимые учащимся новые знания. Формируются следующие образующие эту компетенцию умения: самостоятельно ставить учебную задачу (цель), разбивать её на составные части, на которых будет основываться процесс её решения, анализировать результат действия, выявлять допущенные ошибки и неточности, исправлять их и представлять полученный результат в форме, легко доступной для восприятия других людей.

Общекультурная компетенция. Под общекультурной компетенцией понимается осведомленность школьников о математике как элементе общечеловеческой культуры, её месте в системе других наук, а также её роли в развитии представлений человечества о целостной картине мира. Формируются следующие образующие эту компетенцию представления: об уровне развития математики на разных исторических этапах; о высокой практической значимости математики с точки зрения создания и развития материальной культуры человечества, а также о важной роли математики с точки зрения формировании таких важнейших черт личности, как независимость и критичность мышления, воля и настойчивость в достижении цели и др.

Содержание математического образования в основной школе формируется на основе фундаментального ядра школь­ного математического образования. В программе оно пред­ставлено в виде совокупности содержательных разделов, кон­кретизирующих соответствующие блоки фундаментального ядра применительно к основной школе. Программа регламен­тирует объем материала, обязательного для изучения в основ­ной школе, а также дает его распределение между 5—6 и 7—9 классами.

Содержание математического образования в основной школе включает следующие разделы: арифметика, алгебра, функции, вероятность и статистика, геометрия. Наряду с этим в него включены два дополнительных раздела: логика и множества, математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и обще­культурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую ли­нию, пронизывающую все основные разделы содержания ма­тематического образования на данной ступени обучения.

Содержание раздела «Арифметика» служит базой для даль­нейшего изучения учащимися математики, способствует разви­тию их логического мышления, формированию умения поль­зоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие поня­тия о числе в основной школе связано с рациональными и ир­рациональными числами, формированием первичных пред­ставлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования.

Содержание раздела «Алгебра» направлено на формирова­ние у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружа­ющей реальности. Язык алгебры подчеркивает значение мате­матики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для усвоения курса информатики, овладения навыками дедуктивных рассуждений. Преобразова­ние символьных форм вносит специфический вклад в разви­тие воображения учащихся, их способностей к математическо­му творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с ир­рациональными выражениями, с тригонометрическими функ­циями и преобразованиями, входят в содержание курса мате­матики на старшей ступени обучения в школе.

Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разно­образных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вно­сит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.

Раздел «Вероятность и статистика» — обязательный ком­понент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим прежде всего для формирования у учащихся функциональной грамот­ности — умений воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, про­водить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащимся рассматривать случаи, осуществлять перебор и подсчет числа вариантов, в том чис­ле в простейших прикладных задачах.

При изучении статистики и вероятности расширяются представления о современной картине мира и методах его ис­следования, формируется понимание роли статистики как ис­точника социально значимой информации и закладываются основы вероятностного мышления.

Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изуча­ется и используется распределенно — в ходе рассмотрения различных вопросов курса. Соответствующий материал наце­лен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи.

Раздел «Математика в историческом развитии» предназна­чен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролиру­ется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рас­смотрении проблематики основного содержания математичес­кого образования.

Ценностные ориентиры содержания учебного предмета

Математическое образование играет важную роль как в практической, так и в духовной жизни общества. Практическая сторона математического образования связана с формировани­ем способов деятельности, духовная — с интеллектуальным развитием человека, формированием характера и общей куль­туры.

Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реально­го мира: пространственные формы и количественные отноше­ния — от простейших, усваиваемых в непосредственном опы­те, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математиче­ских знаний затруднено понимание принципов устройства и ис­пользования современной техники, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится вы­полнять достаточно сложные расчеты, находить в справочниках нужные формулы и применять их, владеть практическими прие­мами геометрических измерений и построений, читать инфор­мацию, представленную в виду таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, со­ставлять несложные алгоритмы и др.

Без базовой математической подготовки невозможно стать образованным современным человеком. В школе математика служит опорным предметом для изучения смежных дисцип­лин. В послешкольной жизни реальной необходимостью в наши дни является непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И, наконец, все больше специально­стей, где необходим высокий уровень образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, био­логия, психология и др.). Таким образом, расширяется круг школьников, для которых математика становится значимым предметом.

Для жизни в современном обществе важным является формирование математического стиля мышления, проявляю­щегося в определенных умственных навыках. В процессе ма­тематической деятельности в арсенал приемов и методов че­ловеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построе­ний, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мыш­ление. Ведущая роль принадлежит математике в формирова­нии алгоритмического мышления и воспитании умений дей­ствовать по заданному алгоритму и конструировать новые. В ходе решения задач — основной учебной деятельности на уроках математики — развиваются творческая и прикладная стороны мышления.

Обучение математике дает возможность развивать у уча­щихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, сим­волические, графические) средства.

Математическое образование вносит свой вклад в форми­рование общей культуры человека. Необходимым компонен­том общей культуры в современном толковании является об­щее знакомство с методами познания действительности, представление о предмете и методе математики, его отличия от методов естественных и гуманитарных наук, об особенно­стях применения математики для решения научных и при­кладных задач.

Изучение математики способствует эстетическому воспита­нию человека, пониманию красоты и изящества математиче­ских рассуждений, восприятию геометрических форм, усвое­нию идеи симметрии.

История развития математического знания дает возмож­ность пополнить запас историко-научных знаний школьни­ков, сформировать у них представления о математике как ча­сти общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математи­ческой науки, с историей великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.

Описание места учебного предмета в учебном плане

В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования в 7–9 классах предмет «Математика» делится на два предмета: «Алгебра» и «Геометрия». Общее количество уроков алгебры в неделю в 7-8 классах по 4 часа (3 часа по учебному плану + 1 час из части, формируемой участниками образовательных отношений), в 9 классе – по 3 часа; в году 7-8 классах – по 136 часов, в 9 классе – 102 часа, за курс 7-9 класс всего 374 часа. Распределение учебного времени представлено в таблице.

Курс	Количество часов в неделю	Количество часов в год
Алгебра, 7 класс	4	136
Алгебра, 8 класс	4	136
Алгебра, 9 класс	3	102
ИТОГО		374

№	Раздел курса	По авторской программе (кол-во часов)	По рабочей программе (кол-во часов)	7 класс	8 класс	9 класс
	Линейное уравнение с одной переменной	17	17	17
	Целые выражения	68	68	68
	Функции	18	18	18
	Системы линейных уравнений с двумя переменными	25	25	25
	Рациональные выражения	55	55		55
	Квадратные корни. Действительные числа	30	30		30
	Квадратные уравнения	36	36		36
	Неравенства	21	21			21
	Квадратичная функция	32	32			32
	Элементы прикладной математики	21	21			21
	Числовые последовательности	21	21			21
	Повторение и систематизация учебного материала	41	30	8	15	7
Итого		385	374	136	136	102

Описание материально-технического обеспечения образовательной деятельности

Дидактическое и методическое обеспечение

Дидактическое обеспечение

Методическое обеспечение

Алгебра – 7 класс:дидактические материалы: пособие для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, Е.М.Рабинович, М.С.Якир. – М.: Вентана – Граф, 2013. Алгебра – 8 класс:дидактические материалы: пособие для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, Е.М.Рабинович, М.С.Якир. – М.: Вентана – Граф, 2013. Алгебра – 9 класс: дидактические материалы: пособие для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, Е.М.Рабинович, М.С.Якир. – М.: Вентана – Граф, 2014.

Федеральный государственный образовательный стандарт общего образования. Примерные программы основного общего образования. Математика.-(Стандарты второго поколения).-М: Просвещение, 2010. Устные занятия по математике в старших классах. Пособие для учителя. А.Я.Кононов/ «Столетие»/Москва, 1997 Обощающее повторение в курсе алгебры основной школы/ Е.А.Семенко/Краснодар:КубГУ, 2002 Основы статистики и вероятность/ Е.А.Бунимович/Москва: Дрофа, 2008 Математика в ребусах, кроссвордах, чайнвордах, криптограммах, 7 класс/С.С.Худадава/Москва: Школьная пресса, 2003 («Библиотека журнала «Математика в школе» вып.23) Пичурин Л.Ф. За страницами учебника алгебры/ Л.Ф.Пичурин. – М: Просвещение, 1991. Формирование вычислительных навыков на уроках математики 5-9 классы/Н.Н.Хлевнюк/ М.:Илекса, 2011 Алгебра – 7 класс: учебник для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2012. Алгебра – 7 класс: методическое пособие/ Е.В.Буцко, А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2013. Алгебра – 8 класс: учебник для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2012. Алгебра – 8 класс: методическое пособие/ Е.В.Буцко, А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2013. Алгебра – 9 класс: учебник для учащихся общеобразовательных учреждений/ А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2014. Алгебра – 9 класс: методическое пособие/ Е.В.Буцко, А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М.: Вентана – Граф, 2014.

Материально-техническое обеспечение

Наименование объектов и средства материально-технического обеспечения	Количество	Примечание
Мультимедийный компьютер Мультимедиапроектор Интерактивная доска Таблицы по математике (комплект) Портреты выдающихся деятелей математики (комплект) Комплект чертёжных инструментов, комплекты планиметрических и стереометрических тел (демонстрационных и раздаточных)	1 1 1 1 1 1

Информационно-коммуникационные средства

Видеофильмы	Электронные образовательные ресурсы	Ресурсы Интернета
Видеофильм "Геометрия Эвклида" Видеофильм "От Архимеда до наших дней" Видеофильм "Этюды о русских ученых"	Мультимедийные обучающие программы и электронные учебные издания по основным разделам курса математики	http://school-collection.edu.ru/ http://www.bymath.net/ http://www.mathematics.ru/ http://www.mathtest.ru/ http://www.ege.edu.ru/ http://uztest.ru/ http://schoolmathematics.ru/ http://shpargalkaege.ru/ http://college.ru/matematika/ http://ege.yandex.ru/mathematic http://ege.yandex.ru/mathematic http://mathege.ru/or/ege/Main/ http://mathgia.ru/or/gia12/Main/ http://www.math-on-line.com/ http://mathkang.ru/ http://www.zaba.ru/ http://festival.1september.ru/articles/subjects/1 http://www.edcommunity.ru/ http://www.problems.ru/ http://www.pm298.ru/ http://www.math.ru/ http://www.allmath.ru/ http://Math-Net.ru/ http://www.uchportal.ru/ http://www.mccme.ru/ http://www.exponenta.ru/ http://fipi.ru/ http://alexlarin.net/

II. планируемые результаты ОСВОЕНИЯ учебного предмета «алгебра»

Алгебраические выражения

Выпускник научится:

• оперировать понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;

• выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;

• выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;

• выполнять разложение многочленов на множители.

Выпускник получит возможность научиться:

• выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приемов;

• применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).

Уравнения

Выпускник научится:

• решать основные виды рациональных уравнений с одной переменной, системы двух уравнений с двумя переменными;

• понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;

• применять графические представления для исследования уравнений, исследования и решения систем уравнений с двумя переменными.

Выпускник получит возможность:

• овладеть специальными приемами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;

• применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.

Неравенства

Выпускник научится:

• понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;

• решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;

• применять аппарат неравенств для решения задач из различных разделов курса.

Выпускник получит возможность научиться:

• разнообразным приемам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;

• применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.

Основные понятия. Числовые функции

Выпускник научится:

• понимать и использовать функциональные понятия и язык (термины, символические обозначения);

• строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;

• понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.

Выпускник получит возможность научиться:

• проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно заданные, с выколотыми точками и т. п.);

использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.

Числовые последовательности

Выпускник научится:

• понимать и использовать язык последовательностей (термины, символические обозначения);

• применять формулы, связанные с арифметической и геометрической прогрессий, и понятийный аппарат, сформированный при изучении других разделов курса, к решению задач, в том числе с контекстом из реальной жизни.

Выпускник получит возможность научиться:

• решать комбинированные задачи с применением формул n-го члена и суммы первых n членов арифметической и геометрической прогрессии, применяя при этом аппарат уравнений и неравенств;

• понимать арифметическую и геометрическую прогрессию как функции натурального аргумента; связывать арифметическую прогрессию с линейным ростом, геометрическую — с экспоненциальным ростом.

Описательная статистика

Выпускник научится использовать простейшие способы представления и анализа статистических данных.

Выпускник получит возможность приобрести первоначальный опыт организации сбора данных при проведении опроса общественного мнения, осуществлять их анализ, представлять результаты опроса в виде таблицы, диаграммы.

Случайные события и вероятность

Выпускник научится находить относительную частоту и вероятность случайного события.

Выпускник получит возможностьприобрести опыт проведения случайных экспериментов, в том числе, с помощью компьютерного моделирования, интерпретации их результатов.

Комбинаторика

Выпускник научится решать комбинаторные задачи на нахождение числа объектов или комбинаций.

Выпускник получит возможностьнаучиться некоторым специальным приемам решения комбинаторных задач.

РАБОТА С ОДАРЕННЫМИ ДЕТЬМИ.

На уроках проводится работа с одаренными детьми (дифференциация и индивидуализация в обучении):

- разноуровневые задания (обучающие и контролирующие);

- обучение самостоятельной работе (работа самостоятельно с учебником, с дополнительной литературой);

- развивающие задачи, в том числе олимпиадные задачи;

- творческие задания (составить задачу, выражение, кроссворд, ребус, анаграмму и т. д.).

Личностные, метапредметные и предметные результаты освоения учебного предмета

Содержание и методический аппарат учебников способствуют формированию у учащихся личностных, метапредметных, предметных результатов обучения, соответствующих требованиям федерального государственного образовательного стандарта основного общего образования.

Изучение нового содержания в учебниках сопровождается рассмотрением задач как практического, так и теоретического характера. В учебниках представлена рубрика «Готовимся к изучению новой темы», в которой содержатся необходимые для изучения нового материала задачи, даются рекомендации по подготовке к изучению нового материала(повторению необходимых сведений из пройденного). Это позволяет обучающимся определять цели своего обучения, ставить и формулировать для себя новые задачи в учебе.

Упражнения каждого параграфа составляют нескольких рубрик: «Решаем устно», «Упражнения», «Упражнения для повторения», «Готовимся к изучению новой темы», «Учимся делать нестандартные шаги». Система заданий представлена упражнениями различной сложности (четыре уровня сложности), ориентирующими на различные формы деятельности, что помогает учащимся в выборе индивидуальной образовательной траектории.

В конце глав приведены итоги, в которых перечислены планируемые результаты обучения; даны задания в тестовой форме «Проверь себя».

Умение создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации позволяют формировать задания на установление верности утверждения, а также на представление данных в виде таблиц, графиков, диаграмм, на работу с этими данными.

Раздел «Дружим с компьютером», полностью интегрированный и с содержанием учебника, и с содержанием дидактического материала к нему, позволяет учителю организовать учебный процесс на современном уровне с использованием ИКТ.

Личностные результаты:

1. воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

2. ответственное отношение к учению, готовность и спо­собность обучающихся к саморазвитию и самообразова­нию на основе мотивации к обучению и познанию;

3. осознанный выбор и построение дальнейшей индивиду­альной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а так­же на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

4. умение контролировать процесс и результат учебной и математической деятельности;

5. критичность мышления, инициатива, находчивость, активность при решении математических задач.

Метапредметные результаты:

1. умение самостоятельно определять цели своего обуче­ния, ставить и формулировать для себя новые задачи в учёбе, развивать мотивы и интересы своей познава­тельной деятельности;

2. умение соотносить свои действия с планируемыми ре­зультатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требова­ний, корректировать свои действия в соответствии с из­меняющейся ситуацией;

1. умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;

2. умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индук­тивное, дедуктивное и по аналогии) и делать выводы;

3. развитие компетентности в области использования ин­формационно-коммуникационных технологий;

4. первоначальные представления об идеях и о методах математики как об универсальном языке науки и тех­ники, о средстве моделирования явлений и процессов;

5. умение видеть математическую задачу в контексте про­блемной ситуации в других дисциплинах, в окружаю­щей жизни;

6. умение находить в различных источниках информа­цию, необходимую для решения математических про­блем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;

7. умение понимать и использовать математические сред­ства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

1. умение выдвигать гипотезы при решении задачи, пони­мать необходимость их проверки;

2. понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

В том числе:

Регулятивные УУД:

7–9-й классы

– самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности;

– выдвигать версии решения проблемы, осознавать конечный результат, выбирать средства достижения цели из предложенных или их искать самостоятельно;

– составлять (индивидуально или в группе) план решения проблемы (выполнения проекта);

– подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель;

– работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер);

– планировать свою индивидуальную образовательную траекторию;

– работать по самостоятельно составленному плану, сверяясь с ним и с целью деятельности, исправляя ошибки, используя самостоятельно подобранные средства (в том числе и Интернет);

– свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся критериев, различая результат и способы действий;

– в ходе представления проекта давать оценку его результатам;

– самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;

– уметь оценить степень успешности своей индивидуальной образовательной деятельности;

– давать оценку своим личностным качествам и чертам характера («каков я»), определять направления своего развития («каким я хочу стать», «что мне для этого надо сделать»).

Средством формирования регулятивных УУД служат технология системно-деятельностного подхода на этапе изучения нового материала и технология оценивания образовательных достижений (учебных успехов).

Познавательные УУД:

7–9-й классы

– анализировать, сравнивать, классифицировать и обобщать факты и явления;

– осуществлять сравнение, сериацию и классификацию, самостоятельно выбирая основания и критерии для указанных логических операций; строить классификацию путём дихотомического деления (на основе отрицания);

– строить логически обоснованное рассуждение, включающее установление причинно-следственных связей;

– создавать математические модели;

– составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.);

– вычитывать все уровни текстовой информации.

– уметь определять возможные источники необходимых сведений, производить поиск формации, анализировать и оценивать её достоверность.

– понимая позицию другого человека, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории. Для этого самостоятельно использовать различные виды чтения (изучающее, просмотровое, ознакомительное, поисковое), приёмы слушания.

– самому создавать источники информации разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности;

– уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей. Уметь выбирать адекватные задаче инструментальные программно-аппаратные средства и сервисы.

Средством формирования познавательных УУД служат учебный материал и прежде всего продуктивные задания учебника.

– Использование математических знаний для решения различных математических задач и оценки полученных результатов.

– Совокупность умений по использованию доказательной математической речи.

– Совокупность умений по работе с информацией, в том числе и с различными математическими текстами.

– Умения использовать математические средства для изучения и описания реальных процессов и явлений.

– Независимость и критичность мышления.

– Воля и настойчивость в достижении цели.

Коммуникативные УУД:

7–9-й классы

– самостоятельно организовывать учебное взаимодействие в группе (определять общие цели, договариваться друг с другом и т.д.);

– отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами;

– в дискуссии уметь выдвинуть контраргументы;

– учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

– понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;

– уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Средством формирования коммуникативных УУД служат технология проблемного обучения, организация работы в малых группах, также использование на уроках технологии личностно - ориентированного и системно-деятельностного обучения.

Предметные результаты:

1. осознание значения математики для повседневной жиз­ни человека;

2. представление о математической науке как сфере мате­матической деятельности, об этапах её развития, о её значимости для развития цивилизации;

1. развитие умений работать с учебным математическим текстом (анализировать, извлекать необходимую ин­формацию), точно и грамотно выражать свои мысли с применением математической терминологии и симво­лики, проводить классификации, логические обосно­вания;

2. владение базовым понятийным аппаратом по основным разделам содержания;

3. практически значимые математические умения и навы­ки, их применение к решению математических и нема­тематических задач, предполагающее умения:

• выполнять вычисления и действия с действительными числами;

• решать уравнения, неравенства, системы уравнений и неравенств;

• решать текстовые задачи арифметическим способом и с помощью составления и решения уравнений, систем уравнений и неравенств;

• изображать фигуры на плоскости;

• использовать алгебраический «язык» для описания предметов окружающего мира;

• производить практические расчёты; вычисления с процентами, вычисления с числовыми последовательностями;

• выполнять тождественные преобразования рациональных выражений;

• выполнять операции над множествами;

• исследовать функции и строить их графики;

• читать и использовать информацию, представлен­ную в виде таблицы, диаграммы (столбчатой или круговой), в графическом виде;

• решать простейшие комбинаторные задачи.

III. Содержание учебного предмета «алгебра»

Алгебра, 7 класс

Глава 1. Линейное уравнение с одной переменной (17 ч.)

• Введение в алгебру. Линейное уравнение с одной переменной.

• Решение задач с помощью уравнений.

Глава 2. Целые выражения(68 ч.)

• Тождественно равные выражения. Тождества

• Степень с натуральным показателем. Свойства степени с натуральным показателем

• Одночлены. Многочлены.

• Сложение и вычитание многочленов. Умножение одночлена на многочлен. Умножение многочлена на многочлен.

• Разложение многочленов на множители. Вынесение общего множителя за скобки. Метод группировки.

• Произведение разности и суммы двух выражений. Разность квадратов двух выражений. Квадрат суммы и квадрат разности двух выражений. Сумма и разность кубов двух выражений.

Глава 3. Функции(18 ч.)

• Связи между величинами. Функция.

• Способы задания функции. График функции.

Глава 4. Системы линейных уравнений с двумя переменными (25 ч.)

• Уравнения с двумя переменными. Линейное уравнение с двумя переменными и его график.

•. Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными. Решение систем линейных уравнений методом подстановки. Решение систем линейных уравнений методом сложения. Решение задач с помощью систем уравнений.

Алгебра, 8 класс

Глава 1. Рациональные выражения (55 ч.)

• Рациональные дроби. Основное свойство рациональной дроби.

• Сложение и вычитание рациональных дробей с одинаковыми знаменателями. Сложение и вычитание рациональных дробей с разными знаменателями. Тождественные преобразования рациональных выражений

• Умножение и деление рациональных дробей. Возведение рациональной дроби в степень. Тождественные преобразования рациональных выражений

• Рациональные уравнения. Равносильные уравнения.

• Степень с целым отрицательным показателем. Свойства степени с целым показателем

• Функция 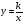и её график

Глава 2. Квадратные корни. Действительные числа (30 ч.)

• Функция y = x² и её график

• Квадратные корни. Арифметический квадратный корень. Свойства арифметического квадратного корня. Тождественные преобразования выражений, содержащих квадратные корни.

• Множество и его элементы.

• Подмножество. Операции над множествами.

• Функция 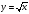и её график

Глава 3. Квадратные уравнения (36 ч.)

• Квадратные уравнения. Решение неполных квадратных уравнений. Формула корней квадратного уравнения. Теорема Виета.

• Квадратный трёхчлен.

Алгебра 9 класс.

Глава 1. Неравенства (21 ч.)

• Числовые неравенства. Основные свойства числовых неравенств. Сложение и умножение числовых неравенств. Оценивание значения выражения

• Неравенства с одной переменной. Решение неравенств с одной переменной. Числовые промежутки. Системы линейных неравенств с одной переменной.

Глава 2. Квадратичная функция (32 ч.)

• Повторение и расширение сведений о функции. Свойства функции.

• Как построить график функции y = kf(x), если известен график функции y = f(x).

• Как построить графики функций y = f(x) + b и y = f(x + a), если известен график функции y = f(x).

• Квадратичная функция, её график и свойства. Решение квадратных неравенств.

• Решение задач с помощью систем уравнений второй степени

Глава 3. Элементы прикладной математики (21 ч.)

• Математическое моделирование. Процентные расчёты. Приближённые вычисления.

• Основные правила комбинаторики. Частота и вероятность случайного события. Классическое определение вероятности. Начальные сведения о статистике.

Глава 4. Числовые последовательности (21 ч.)

• Числовые последовательности. Арифметическая прогрессия. Сумма n первых членов арифметической прогрессии.

•. Геометрическая прогрессия. Сумма n первых членов геометрической прогрессии. Сумма бесконечной геометрической прогрессии, у которой | q |

VI. Тематическое планирование с определением основных видов учебной деятельности обучающихся

7 класс

Номер

параграфа

Содержание учебного
материала

Характеристика основных видов деятельности ученика
(на уровне учебных действий)

Глава 1. Линейное уравнение с одной переменной

17

Распознавать числовые выражения и выражения с переменными, линейные уравнения. Приводить примеры выражений с переменными, линейных уравнений. Составлять выражение с переменными по условию задачи. Выполнять преобразования выражений: приводить подобные слагаемые, раскрывать скобки. Находить значение выражения с переменными при заданных значениях переменных. Классифицировать алгебраические выражения. Описывать целые выражения.

Формулировать определение линейного уравнения. Решать линейное уравнение в общем виде. Интерпретировать уравнение как математическую модель реальной ситуации. Описывать схему решения текстовой задачи, применять её для решения задач

1

Введение в алгебру

3

2

Линейное уравнение с одной переменной

6

3

Решение задач с помощью уравнений

6

Повторение

и систематизация

учебного материала

1

Контрольная работа № 1 «Линейное уравнение с одной переменной»

1

Глава 2. Целые выражения

68

Формулировать:

определения: тождественно равных выражений, тождества, степени с натуральным показателем, одночлена, стандартного вида одночлена, коэффициента одночлена, степени одночлена, многочлена, степени многочлена;

свойства: степени с натуральным показателем, знака степени;

правила: доказательства тождеств, умножения одночлена на многочлен, умножения многочленов.

Доказывать свойства степени с натуральным показателем. Записывать и доказывать формулы: произведения суммы и разности двух выражений, разности квадратов двух выражений, квадрата суммы и квадрата разности двух выражений, суммы кубов и разности кубов двух выражений.

Вычислять значение выражений с переменными. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночлена в степень. Приводить одночлен к стандартному виду. Записывать многочлен в стандартном виде, определять степень многочлена. Преобразовывать произведение одночлена и многочлена; суммы, разности, произведения двух многочленов в многочлен. Выполнять разложение многочлена на множители способом вынесения общего множителя за скобки, способом группировки, по формулам сокращённого умножения и с применением нескольких способов. Использовать указанные преобразования в процессе решения уравнений, доказательства утверждений, решения текстовых задач

4

Тождественно равные выражения. Тождества

3

5

Степень с натуральным показателем

3

6

Свойства степени с натуральным показателем

4

7

Одночлены

3

8

Многочлены

2

9

Сложение и вычитание многочленов

3

Повторение

и систематизация

учебного материала

1

Контрольная работа № 2 «Одночлены. Многочлены. Сложение и вычитание многочленов».

1

10

Умножение одночлена на многочлен

5

11

Умножение многочлена на многочлен

5

12

Разложение многочленов на множители. Вынесение общего множителя за скобки

4

13

Разложение многочленов на множители. Метод группировки

4

Повторение

и систематизация

учебного материала

1

Контрольная работа № 3 «Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители».

1

14

Произведение разности и суммы двух выражений

4

15

Разность квадратов двух выражений

4

16

Квадрат суммы и квадрат разности двух выражений

4

17

Преобразование многочлена в квадрат суммы или разности двух выражений

4

Повторение

и систематизация

учебного материала

1

Контрольная работа № 4 «Формулы сокращенного умножения»

1

18

Сумма и разность кубов двух выражений

2

19

Применение различных способов разложения многочлена на множители

5

Повторение и систематизация

учебного материала

2

Контрольная работа № 5 «Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на множители»

1

Глава 3. Функции

18

Приводить примеры зависимостей между величинами. Различать среди зависимостей функциональные зависимости.

Описывать понятия: зависимой и независимой переменных, функции, аргумента функции; способы задания функции. Формулировать определения: области определения функции, области значений функции, графика функции, линейной функции, прямой пропорциональности.

Вычислять значение функции по заданному значению аргумента. Составлять таблицы значений функции. Строить график функции, заданной таблично. По графику функции, являющейся моделью реального процесса, определять характеристики этого процесса. Строить график линейной функции и прямой пропорциональности. Описывать свойства этих функций

20

Связи между величинами. Функция

3

21

Способы задания функции

3

22

График функции

3

23

Линейная функция, её график и свойства

6

Повторение и систематизация

учебного материала

2

Контрольная работа № 6 «Функции»

1

Глава 4. Системы линейных уравнений

с двумя переменными

25

Приводить примеры: уравнения с двумя переменными; линейного уравнения с двумя переменными; системы двух линейных уравнений с двумя переменными; реальных процессов, для которых уравнение с двумя переменными или система уравнений с двумя переменными являются математическими моделями.

Определять, является ли пара чисел решением данного уравнения с двумя переменными.

Формулировать:

определения: решения уравнения с двумя переменными; что значит решить уравнение с двумя переменными; графика уравнения с двумя переменными; линейного уравнения с двумя переменными; решения системы уравнений с двумя переменными;

свойства уравнений с двумя переменными.

Описывать: свойства графика линейного уравнения в зависимости от значений коэффициентов, графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения для решения системы двух линейных уравнений с двумя переменными.

Строить график линейного уравнения с двумя переменными. Решать системы двух линейных уравнений с двумя переменными.

Решать текстовые задачи, в которых система двух линейных уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы

24

Уравнения с двумя переменными

3

25

Линейное уравнение с двумя переменными и его график

3

26

Системы уравнений с двумя переменными. Графический метод решения системы двух линейных уравнений с двумя переменными

3

27

Решение систем линейных уравнений методом подстановки

4

28

Решение систем линейных уравнений методом сложения

5

29

Решение задач с помощью систем линейных уравнений

5

Повторение и систематизация

учебного материала

1

Контрольная работа № 7 «Системы линейных уравнений с двумя переменными»

1

Повторение и систематизация учебного материала

8

Упражнения для повторения курса 7 класса

6

Итоговая контрольная работа

2

Итого:

136

8 класс

Номер

параграфа

Содержание учебного
материала

Характеристика основных видов деятельности ученика
(на уровне учебных действий)

Глава 1. Рациональные выражения

55

Распознавать целые рациональные выражения, дробные рациональные выражения, приводить примеры таких выражений.

Формулировать:

определения: рационального выражения, допустимых значений переменной, тождественно равных выражений, тождества, равносильных уравнений, рационального уравнения, степени с нулевым показателем, степени с целым отрицательным показателем, стандартного вида числа, обратной пропорциональности;

свойства: основное свойство рациональной дроби, свойства степени с целым показателем, уравнений, функции ;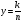

правила: сложения, вычитания, умножения, деления дробей, возведения дроби в степень; условие равенства дроби нулю.

Доказывать свойства степени с целым показателем.

Описывать графический метод решения уравнений с одной переменной.

Применять основное свойство рациональной дроби для сокращения и преобразования дробей. Приводить дроби к новому (общему) знаменателю. Находить сумму, разность, произведение и частное дробей. Выполнять тождественные преобразования рациональных выражений.

Решать уравнения с переменной в знаменателе дроби.

Применять свойства степени с целым показателем для преобразования выражений.

Записывать числа в стандартном виде.

Выполнять построение и чтение графика функции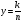

1

Рациональные дроби

3

2

Основное свойство рациональной дроби

4

3

Сложение и вычитание рациональных дробей с одинаковыми знаменателями

4

4

Сложение и вычитание рациональных дробей с разными знаменателями

7

Контрольная работа № 1 «Основное свойство дроби. Сложение и вычитание дробей с разными знаменателями»

1

5

Умножение и деление рациональных дробей. Возведение рациональной дроби в степень

5

6

Тождественные преобразования рациональных выражений

8

Контрольная работа № 2 «Умножение и деление рациональных дробей. Возведение рациональной дроби в степень»

1

7

Равносильные уравнения.

Рациональные уравнения

5

8

Степень с целым отрицательным показателем

5

9

Свойства степени с целым показателем

6

10

Функция 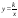и её график

5

Контрольная работа № 3 «Свойства степени с целым показателем»

1

Глава 2. Квадратные корни.

Действительные числа

30

Описывать: понятие множества, элемента множества, способы задания множеств; множество натуральных чисел, множество целых чисел, множество рациональных чисел, множество действительных чисел и связи между этими числовыми множествами; связь между бесконечными десятичными дробями и рациональными, иррациональными числами.

Распознавать рациональные и иррациональные числа. Приводить примеры рациональных чисел и иррациональных чисел.

Записывать с помощью формул свойства действий с действительными числами.

Формулировать:

определения: квадратного корня из числа, арифметического квадратного корня из числа, равных множеств, подмножества, пересечения множеств, объединения множеств;

свойства: функции y = x², арифметического квадратного корня, функции .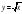

Доказывать свойства арифметического квадратного корня.

Строить графики функций y = x² и .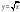

Применять понятие арифметического квадратного корня для вычисления значений выражений.

Упрощать выражения. Решать уравнения. Сравнивать значения выражений. Выполнять преобразование выражений с применением вынесения множителя из-под знака корня, внесение множителя под знак корня. Выполнять освобождение от иррациональности в знаменателе дроби, анализ соотношений между числовыми множествами и их элементами

11

Функция y = x² и её график

3

12

Квадратные корни. Арифметический квадратный корень

4

13

Множество и его элементы

2

14

Подмножество. Операции над множествами

2

15

Числовые множества

2

16

Свойства арифметического квадратного корня

6

17

Тождественные преобразования выражений, содержащих

квадратные корни

7

18

Функция 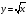и её график

3

Контрольная работа № 4 «Квадратные корни.

Действительные числа»

1

Глава 3. Квадратные уравнения

36

Распознавать и приводить примеры квадратных уравнений различных видов (полных, неполных, приведённых), квадратных трёхчленов.

Описывать в общем виде решение неполных квадратных уравнений.

Формулировать:

определения: уравнения первой степени, квадратного уравнения; квадратного трёхчлена, дискриминанта квадратного уравнения

и квадратного трёхчлена, корня квадратного трёхчлена; биквадратного уравнения;

свойства квадратного трёхчлена;

теорему Виета и обратную ей теорему.

Записывать и доказывать формулу корней квадратного уравнения. Исследовать количество корней квадратного уравнения в зависимости от знака его дискриминанта.

Доказывать теоремы: Виета (прямую и обратную), о разложении квадратного трёхчлена на множители, о свойстве квадратного трёхчлена с отрицательным дискриминантом.

Описывать на примерах метод замены переменной для решения уравнений.

Находить корни квадратных уравнений различных видов. Применять теорему Виета и обратную ей теорему. Выполнять разложение квадратного трёхчлена на множители. Находить корни уравнений, которые сводятся к квадратным. Составлять квадратные уравнения и уравнения, сводящиеся к квадратным, являющиеся математическими моделями реальных ситуаций

19

Квадратные уравнения. Решение неполных квадратных уравнений

5

20

Формула корней квадратного уравнения

6

21

Теорема Виета

5

Контрольная работа № 5 «Решение квадратных уравнений»

1

22

Квадратный трёхчлен

5

23

Решение уравнений, которые сводятся к квадратным уравнениям

6

24

Рациональные уравнения как математические модели реальных ситуаций

7

Контрольная работа № 6 «Рациональные уравнения как математические модели реальных ситуаций»

1

Повторение и систематизация

учебного материала

15

Упражнения для повторения курса 8 класса

13

Контрольная работа № 7

2

9 класс

Номер

параграфа

Содержание учебного
материала

Характеристика основных видов деятельности ученика
(на уровне учебных действий)

Глава 1. Неравенства

21

Распознавать и приводить примеры числовых неравенств, неравенств с переменными, линейных неравенств с одной переменной, двойных неравенств.

Формулировать:

определения: сравнения двух чисел, решения неравенства с одной переменной, равносильных неравенств, решения системы неравенств с одной переменной, области определения выражения;

свойства числовых неравенств, сложения и умножения числовых неравенств

Доказывать: свойства числовых неравенств, теоремы о сложении и умножении числовых неравенств.

Решать линейные неравенства. Записывать решения неравенств и их систем в виде числовых промежутков, объединения, пересечения числовых промежутков. Решать систему неравенств с одной переменной. Оценивать значение выражения. Изображать на координатной прямой заданные неравенствами числовые промежутки

1

Числовые неравенства

3

2

Основные свойства числовых неравенств

2

3

Сложение и умножение числовых неравенств. Оценивание значения выражения

3

4

Неравенства с одной переменной

1

5

Решение неравенств с одной переменной. Числовые промежутки

5

6

Системы линейных неравенств с одной переменной

6

Контрольная работа № 1 «Неравенства»

1

Глава 2. Квадратичная функция

32

Описывать понятие функции как правила, устанавливающего связь между элементами двух множеств.

Формулировать:

определения: нуля функции; промежутков знакопостоянства функции; функции, возрастающей (убывающей) на множестве; квадратичной функции; квадратного неравенства;

свойства квадратичной функции;

правила построения графиков функций с помощью преобразований вида f(x) → f(x)+а;

f(x) → f(x + а); f(x) → kf(x).

Строить графики функций с помощью преобразований вида f(x) → f(x)+ а;

f(x) → f(x + а); f(x) → kf(x).

Строить график квадратичной функции. По графику квадратичной функции описывать её свойства.

Описывать схематичное расположение параболы относительно оси абсцисс в зависимости от знака старшего коэффициента и дискриминанта соответствующего квадратного трёхчлена.

Решать квадратные неравенства, используя схему расположения параболы относительно оси абсцисс.

Описывать графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения для решения системы двух уравнений с двумя переменными, одно из которых не является линейным.

Решать текстовые задачи, в которых система двух уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы

7

Повторение и расширение сведений о функции

3

8

Свойства функции

3

9

Как построить график функции y = kf(x), если известен график функции y = f(x)

2

10

Как построить графики функций y = f(x) + b
и y = f(x + a), если известен график функции y = f(x)

3

11

Квадратичная функция, её график и свойства

5

Контрольная работа № 2 «Квадратичная функция, её график и свойства»

1

12

Решение квадратных неравенств

5

13

Системы уравнений с двумя переменными

5

14

Решение задач с помощью систем уравнений второй степени

4

Контрольная работа № 3 «Квадратные неравенства. Системы уравнений с двумя переменными»

1

Глава 3. Элементы прикладной математики

21

15

Математическое моделирование

3

Приводить примеры:

математических моделей реальных ситуаций; прикладных задач; приближённых величин; использования комбинаторных правил суммы и произведения; случайных событий, включая достоверные и невозможные события; опытов с равновероятными исходами; представления статистических данных в виде таблиц, диаграмм, графиков; использования вероятностных свойств окружающих явлений.

Формулировать:

определения: абсолютной погрешности, относительной погрешности, достоверного события, невозможного события; классическое определение вероятности;

правила: комбинаторное правило суммы, комбинаторное правило произведения.

Описывать этапы решения прикладной задачи.

Пояснять и записывать формулу сложных процентов. Проводить процентные расчёты с использованием сложных процентов.

Находить точность приближения по таблице приближённых значений величины. Использовать различные формы записи приближённого значения величины. Оценивать приближённое значение величины.

Проводить опыты со случайными исходами. Пояснять и записывать формулу нахождения частоты случайного события. Описывать статистическую оценку вероятности случайного события. Находить вероятность случайного события в опытах с равновероятными исходами.

Описывать этапы статистического исследования. Оформлять информацию в виде таблиц и диаграмм. Извлекать информацию из таблиц и диаграмм. Находить и приводить примеры использования статистических характеристик совокупности данных: среднее значение, мода, размах, медиана выборки

16

Процентные расчёты

3

17

Приближённые вычисления

2

18

Основные правила комбинаторики

3

19

Частота и вероятность случайного события

3

20

Классическое определение вероятности

3

21

Начальные сведения
о статистике

3

Контрольная работа № 4 «Элементы прикладной математики»

1

Глава 4. Числовые последовательности

21

Приводить примеры: последовательностей; числовых последовательностей, в частности арифметической и геометрической прогрессий; использования последовательностей в реальной жизни; задач, в которых рассматриваются суммы с бесконечным числом слагаемых.

Описывать: понятие последовательности, члена последовательности, способы задания последовательности.

Вычислять члены последовательности, заданной формулой n-го члена или рекуррентно.

Формулировать:

определения: арифметической прогрессии, геометрической прогрессии;

свойства членов геометрической и арифметической прогрессий.

Задавать арифметическую и геометрическую прогрессии рекуррентно.

Записывать и пояснять формулы общего члена арифметической и геометрической прогрессий.

Записывать и доказывать: формулы суммы n первых членов арифметической и геометрической прогрессий; формулы, выражающие свойства членов арифметической и геометрической прогрессий.

Вычислять сумму бесконечной геометрической прогрессии, у которой | q |

22

Числовые последовательности

2

23

Арифметическая прогрессия

4

24

Сумма n первых членов арифметической прогрессии

4

25

Геометрическая прогрессия

4

26

Сумма n первых членов геометрической прогрессии

3

27

Сумма бесконечной геометрической прогрессии, у которой | q |

3

Контрольная работа № 5 «Числовые последовательности»

1

Повторение и систематизация

учебного материала

7

Упражнения для повторения курса 9 класса

5

Контрольная работа № 6

2

V. Календарно-тематическое планирование по учебному предмету

№п/п

№ в теме

Тема урока.

Содержание

Планируемые результаты

Основные виды деятельности

Дата

Корректировка

План

Факт

Предметные

Личностные

Метапредметные

1

2

3

4

5

6

7

8

9

10

Линейное уравнение с одной переменной (17 ч.)

1

1

Введение в алгебру. Числовые выражения.

Простейшие преобразования числовых выражений

Обобщить и систематизировать знания учащихся о целых алгебраических выражениях, закрепить навыки вычисления значений числовых выражений, решения задач с помощью составления числовых выражений

Формировать ответственное отношение к обучению, готовность к саморазвитию и решению творческих задач.

Формировать умение использовать приобретенные знания в практической деятельности

Распознавать числовые выражения и выражения с переменными. Приводить примеры выражений с переменными. Составлять выражение по условию задачи. Выполнять преобразования выражений: приводить подобные слагаемые, раскрывать скобки. Находить значение выражения с переменными при заданных значениях переменных. Классифицировать алгебраические выражения. Описывать целые выражения.

2

2

Введение в алгебру. Целые алгебраические выражения.

Простейшие преобразования алгебраических выражений

3

3

Перевод текста на «алгебраический язык».

Решение задач на составление числовых выражений

4

4

Линейное уравнение с одной переменной.

Определение, распознавание, варианты решений, проверка корней, решение линейных уравнений с одной переменной

Закрепить навыки решения линейных уравнений, формировать навыки решения уравнения с модулем и параметром.

Развивать навыки самостоятельной работы, анализа своей работы

Формировать умение выдвигать гипотезы при решении задач и понимание необходимости их проверки

Распознавать линейные уравнения. Приводить примеры линейных уравнений. Составлять уравнение по условию задачи.

Формулировать определение линейного уравнения. Решать линейное уравнение в общем виде. Интерпретировать уравнение как математическую модель реальной ситуации. Описывать схему решения текстовой задачи, применять её для решения задач

5

5

Решение линейных уравнений с одной переменной.

Рассмотреть какое количество корней может иметь линейное уравнение.

6

6

Решение линейных уравнений с модулем и параметром. Способы решения линейных уравнений с модулем и параметром

7

7

Решение уравнений, сводящихся к линейным уравнениям. Алгоритмы решения уравнений, сводящихся к линейным.

8

8

Решение уравнений, сводящихся к линейным уравнениям. Закрепить навыки решения уравнений

9

9

Решение уравнений, сводящихся к линейным уравнениям. Закрепить навыки решения уравнений

10

10

Решение задач с помощью уравнений.

Рассмотреть схему решения задач с помощью уравнений

Обобщить и систематизировать знания и навыки учащихся о решении задач с помощью уравнения.

Формировать способность осознанного выбора и дальнейшей индивидуальной траектории обучения

Формировать умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.

Составлять уравнение по условию задачи.

Интерпретировать уравнение как математическую модель реальной ситуации. Описывать схему решения текстовой задачи, применять её для решения задач

11

11

Решение задач с помощью уравнений.

Использование схемы решения задач с помощью уравнений

12

12

Решение задач на производительность с помощью уравнений.

Применение формулы производительности при решении задач

13

13

Решение задач на движение с помощью уравнений.

Применение формулы пути при решении задач

14

14

Решение задач с помощью уравнений

Решение задач с использованием темы «Проценты», «Нахождение дроби от числа»

15

15

Решение задач с помощью уравнений

Решение задач с использованием темы «Проценты», «Нахождение дроби от числа»

16

16

Подготовка к контрольной работе. Решение задач.

Повторение и обобщение материала по теме «Линейные уравнения с одной переменной»

17

17

Контрольная работа №1 по теме: «Линейные уравнения с одной переменной».

Целые выражения (68 ч.)

1

Анализ контрольной работы.

Тождественно равные выражения.

Определение и приемы доказательства тождеств.

Закрепить навыки применения тождественных преобразований для доказательства тождеств.

Формировать умение соотносить полученный результат с поставленной целью.

Развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

Формулировать:

определения: тождественно равных выражений, тождества, степени с натуральным показателем, одночлена, стандартного вида одночлена, коэффициента одночлена, степени одночлена, многочлена, степени многочлена;

свойства: степени с натуральным показателем, знака степени;

правила: доказательства тождеств, умножения одночлена на многочлен, умножения многочленов.

Доказывать свойства степени с натуральным показателем. Записывать и доказывать формулы: произведения суммы и разности двух выражений, разности квадратов двух выражений, квадрата суммы и квадрата разности двух выражений, суммы кубов и разности кубов двух выражений.

Вычислять значение выражений с переменными. Применять свойства степени для преобразования выражений. Выполнять умножение одночленов и возведение одночлена в степень. Приводить одночлен к стандартному виду. Записывать многочлен в стандартном виде, определять степень многочлена. Преобразовывать произведение одночлена и многочлена; суммы, разности, произведения двух многочленов в многочлен. Выполнять разложение многочлена на множители способом вынесения общего множителя за скобки, способом группировки, по формулам сокращённого умножения и с применением нескольких способов. Использовать указанные преобразования в процессе решения уравнений, доказательства утверждений, решения текстовых задач

2

Тождественно равные выражения. Тождества

Упрощение выражений при доказательстве тождеств

3

Тождественно равные выражения. Доказательство тождеств. Упрощение выражений при доказательстве тождеств

4

Степень с натуральным показателем

Определение степени с натуральным показателем.

Закрепить навыки применения свойств степени с натуральным показателем.

Формировать умение планировать свои действия в соответствии с учебным заданием.

Развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

5

Нахождение значения выражений, содержащих степень. Выполнение упражнений на нахождение значения выражений, содержащих степень.

6

Нахождение значения выражений, содержащих степень. Выполнение упражнений на нахождение значения выражений, содержащих степень.

7

Свойства степени с натуральным показателем.

Рассмотреть свойства степени, их доказательства

8

Применение свойств степени с натуральным показателем к преобразованию выражений.

Выполнение упражнений на преобразование выражений с использованием свойств степени с натуральным показателем.

9

Применение свойств степени с натуральным показателем к преобразованию выражений. Выполнение упражнений на нахождение значения выражений, содержащих степень.

10

Преобразование выражений, содержащих степень. Использование различных приемов и свойств для преобразования выражений, содержащих степень.

11

Одночлены

Определение одночлена, коэффициент и степень одночлена

Закрепить навыки преобразования выражения в одночлен стандартного вида

Развивать познавательный интерес к математике, навыки самостоятельной работы, анализа своей работы.

Формировать умение соотносить свои действия с планируемыми результатами, корректировать свои действия в соответствии с изменяющейся ситуацией.

12

Стандартный вид одночлена. Приведение одночленов к стандартному виду

13

Преобразование выражения в одночлен стандартного вида. Применение различных приёмов для преобразования выражения в одночлен стандартного вида

14

Многочлены. Определение многочлена

Формировать умение применять сложения и вычитания многочленов для решения математических задач.

Формировать умение планировать свои действия в соответствии с учебным заданием, представлять результат своей деятельности

Формировать умение строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы.

15

Преобразование выражения в многочлен стандартного вида. Применение различных способов приведения выражения в многочлен стандартного вида

16

Сложение и вычитание многочленов. Правила сложения и вычитания многочленов

17

Применение сложения и вычитания многочленов для решения математических задач. Выполнение упражнений

18

Сложение и вычитание многочленов. Упрощение выражений. Выполнение упражнений

19

Повторение и систематизация учебного материала

20

Контрольная работа № 2 по теме «Одночлены. Многочлены. Сложение и вычитание многочленов».

21

Умножение одночлена на многочлен.

Правило умножения одночлена на многочлен

Формировать умение, закрепить навыки умножения одночлена на многочлен.

Формировать умение формулировать собственное мнение, представлять результат своей деятельности.

Формировать умение соотносить свои действия с планируемыми результатами.

22

Применение правила умножения одночлена на многочлен к упрощению выражений. Упрощение выражений, содержащих умножение одночлена на многочлен

23

Умножение одночлена на многочлен. Упрощение выражений. Выполнение упражнений

24

Умножение одночлена на многочлен. Выполнение упражнений

25

Умножение одночлена на многочлен. Выполнение упражнений

26

Умножение многочлена на многочлен. Выполнение упражнений

Формировать умение, закрепить навыки умножения многочлена на многочлен.

Формировать критичность мышления, инициативу, находчивость, активность при решении математических задач.

Формировать умение сравнивать, анализировать, моделировать выбор способов деятельности.

27

Применение правила умножения многочлена на многочлен. Алгоритм умножения многочлена на многочлен

28

Применение правила умножения многочлена на многочлен. Применение алгоритма умножения многочлена на многочлен

29

Упрощение выражений с помощью правила умножения многочлена на многочлен. Выполнение упражнений

30

Упрощение выражений с помощью правила умножения многочлена на многочлен. Выполнение упражнений

31

Разложение многочлена на множители. Правило разложения многочлена на множители с помощью вынесения общего множителя за скобки

Формировать умение, закрепить навыки вынесения общего множителя за скобки.

Формировать соотносить полученный результат с поставленной целью.

Формировать умение осуществлять контроль своей деятельности в процессе достижения результата.

32

Разложение многочлена на множители с помощью метода вынесения общего множителя за скобки. Выполнение упражнений

33

Вынесение общего множителя за скобки. Выполнение упражнений

34

Вынесение общего множителя за скобки. Выполнение упражнений

35

Разложение многочлена на множители. Метод группировки.

Формировать умение, закрепить навыки разложения многочлена на множители методом группировки

Развивать познавательный интерес к математике

Развивать мотивы и интересы своей познавательной деятельности

36

Разложение многочлена на множители методом группировки. Алгоритм разложения на множители методом группировки

37

Метод группировки. Выполнение упражнений

38

Разложение многочлена на множители. Выполнение упражнений

39

Повторение и систематизация учебного материала

40

Контрольная работа № 3 по теме «Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители».

41

Анализ контрольной работы. Произведение разности и суммы двух выражений. Изучение и доказательство формул произведения разности и суммы двух выражений

Формировать умение, закрепить навыки применение правила произведения разности и суммы двух выражений.

Развивать навыки самостоятельной работы, анализа своей работы.

Формировать умение развивать мотивы и интересы своей познавательной деятельности, осуществлять контроль своей деятельности в процессе достижения результата.

42

Произведение разности и суммы двух выражений. Применение формул к выполнению заданий

43

Применение правила произведения разности и суммы двух выражений. Выполнение упражнений

44

Применение правила произведения разности и суммы двух выражений. Формулы сокращенного умножения. Выполнение упражнений

45

Формула разности квадратов двух выражений. Применение формулы для разложения на множители выражений

Формировать умение, закрепить навыки применение формулы сокращенного умножения разности квадратов двух выражений.

Развивать навыки самостоятельной работы, анализа своей работы.

Формировать умение сравнивать, анализировать, моделировать выбор способов деятельности

46

Применение формулы разности квадратов двух выражений. Разложение выражений на множители

47

Формула разности квадратов двух выражений. Применение формулы для разложения на множители выражений

48

Разложение на множители с помощью формулы разности квадратов двух выражений. Выполнение упражнений

49

Вывод формулы квадрата суммы и квадрата разности двух выражений. Первичное закрепление изученного материала

Формировать умение, закрепить навыки применение формул сокращенного умножения квадрата суммы и квадрата разности двух выражений.

Развивать готовность к самообразованию и решению творческих задач.

Формировать умение ставить и формулировать для себя новые задачи в учёбе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности.

50

Применение формулы квадрата суммы и квадрата разности двух выражений. Упрощение выражений

51

Применение формулы квадрата суммы и квадрата разности двух выражений. Упрощение выражений

52

Применение формул сокращенного умножения к преобразованию выражений. Выполнение упражнений

53

Преобразование многочлена в квадрат суммы или разности двух выражений. Разложение выражений на множители

Формировать умение, закрепить навыки преобразования многочлена в квадрат суммы или разности двух выражений.

Развивать готовность к самообразованию и решению творческих задач.

54

Преобразование многочлена в квадрат суммы или разности двух выражений. Разложение выражений на множители

55

Разложение многочлена на множители с помощью формулы квадрата суммы или разности двух выражений. Выполнение упражнений

56

Преобразование многочлена. Выполнение упражнений

57

Повторение и систематизация учебного материала

58

Контрольная работа № 4 по теме «Формулы сокращенного умножения»

59

Анализ контрольной работы. Сумма и разность кубов двух выражений. Вывод формул

Формировать умение, закрепить навыки применение формул суммы и разности кубов двух выражений.

Развивать навыки самостоятельной работы, анализа своей работы.

Формировать умение соотносить свои действия с планируемыми результатами.

60

Сумма и разность кубов двух выражений. Применение формул для разложения на множители

61

Разложение многочлена на множители. Различные способы разложения многочленов на множители

62

Применение различных способов разложения многочлена на множители. Выполнение упражнений

Формировать умение, закрепить навыки применение различных способов разложения многочлена на множители

Формировать умение представлять результат своей деятельности

Формировать умение устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, делать выводы.

63

Применение различных способов разложения многочлена на множители. Выполнение упражнений

64

Применение различных способов для разложения многочлена на множители. Выполнение упражнений

65

Применение различных способов для разложения многочлена на множители. Выполнение упражнений

66

Повторение и систематизация учебного материала из раздела «Целые выражения».

67

Решение задач на подготовку к контрольной работе.

68

Контрольная работа № 5 по теме: «Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на множители».

Функции (18 ч.)

Анализ контрольной работы. Связи между величинами. Функция. Рассмотреть понятие «функция»

Закрепить знания о функции и функциональной зависимости, формировать навыки работы с графиком функции

Формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики

Формировать умение понимать и использовать математические средства наглядности (графики, таблицы)

Приводить примеры зависимостей между величинами. Различать среди зависимостей функциональные зависимости.

Описывать понятия: зависимой и независимой переменных, функции, аргумента функции; способы задания функции. Формулировать определения: области определения функции, области значений функции, графика функции, линейной функции, прямой пропорциональности.

Вычислять значение функции по заданному значению аргумента. Составлять таблицы значений функции. Строить график функции, заданной таблично. По графику функции, являющейся моделью реального процесса, определять характеристики этого процесса. Строить график линейной функции и прямой пропорциональности. Описывать свойства этих функций

Нахождение значения аргумента и значения функции для данной функциональной зависимости. Чтение графиков функций. Выполнение упражнений

Связи между величинами. Функция Выполнение упражнений

Способы задания функции. Описательный способ. Рассмотрение различных способов задания функций

Закрепить знания учащихся о способах задания функции: описательном, с помощью формул, табличном.

Формировать умение планировать свои действия в соответствии с учебным заданием.

Формировать умение ставить и формулировать для себя новые задачи в учебе и познавательной деятельности.

Способ задания функции с помощью формул. Выполнение упражнений

Способ задания функции с помощью формул. Выполнение упражнений

График функции. Определение графика функции

Закрепить знания учащихся о графике функции .

Формировать умение представлять интерес своей деятельности, развивать познавательный интерес к математике.

Формировать умение сравнивать, анализировать, моделировать выбор способов деятельности.

График функции. Определение по графику свойств функции. Рассмотреть свойства функции с помощью графика

График функции. Определение свойств функции с помощью графика

Линейная функция и её график. Определение линейной функции. Название её графика.

Закрепить знания учащихся о линейной функции и её свойствах, формировать навык применения свойств линейной функции при решении задач

Формировать умение использовать приобретенные знания в практической деятельности

Линейная функция и её график. Построение графика линейной функции

Линейная функция и её график. Описание свойств функции. Выявить свойства линейной функции

Применение свойств линейной функции к решению задач. Выполнение упражнений

Применение свойств линейной функции к решению задач. Выполнение упражнений

Применение свойств линейной функции к выполнению заданий повышенной сложности. Выполнение упражнений

Повторение и систематизация учебного матер.

Повторение и систематизация учебного матер.

Контрольная работа № 6 по теме «Функции»

Системы линейных уравнений с двумя переменными (25 ч.)

Анализ контрольной работы. Уравнения с двумя переменными. Рассмотреть уравнения с двумя переменными. Корни уравнения с двумя переменными

Закрепить знания учащихся об уравнениях с двумя переменными.

Формировать умение планировать свои действия в соответствии с учебным заданием.

Формировать умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата.

Приводить примеры: уравнения с двумя переменными; линейного уравнения с двумя переменными; системы двух линейных уравнений с двумя переменными; реальных процессов, для которых уравнение с двумя переменными или система уравнений с двумя переменными являются математическими моделями.

Определять, является ли пара чисел решением данного уравнения с двумя переменными.

Формулировать:

определения: решения уравнения с двумя переменными; что значит решить уравнение с двумя переменными; графика уравнения с двумя переменными; линейного уравнения с двумя переменными; решения системы уравнений с двумя переменными;

свойства уравнений с двумя переменными.

Описывать: свойства графика линейного уравнения в зависимости от значений коэффициентов, графический метод решения системы двух уравнений с двумя переменными, метод подстановки и метод сложения для решения системы двух линейных уравнений с двумя переменными.

Строить график линейного уравнения с двумя переменными. Решать системы двух линейных уравнений с двумя переменными.

Решать текстовые задачи, в которых система двух линейных уравнений с двумя переменными является математической моделью реального процесса, и интерпретировать результат решения системы

Уравнения с двумя переменными. Решение уравнений с двумя переменными

Свойства уравнений с двумя переменными. Применение свойств к решению уравнений

График уравнения с двумя переменными. Построение графика линейного уравнения с двумя переменными

Линейное уравнение с двумя переменными и его график. Построение графика линейного уравнения с двумя переменными

Применение свойств линейного уравнения с двумя переменными к решению задач. Математические модели реальных ситуаций

Системы уравнений с двумя переменными. Ввести понятие системы уравнений с двумя переменными, его решения

Обобщить и систематизировать знания учащихся о системах двух линейных уравнений с двумя переменными. Решение уравнений способом подстановки

Формировать умение соотносить полученный результат с поставленной целью.

Формировать умение сравнивать, анализировать, обобщать по разным показателям, моделировать выбор способов деятельности, группировать.

Графический метод решения систем двух линейных уравнений с двумя переменными. Решение систем двух уравнений графическим методом

Решение систем двух линейных уравнений с двумя переменными с помощью графиков. Выполнение упражнений

Решение систем линейных уравнений методом подстановки. Алгоритм решения систем методом подстановки

Решение систем линейных уравнений методом подстановки. Применение алгоритма решения систем методом подстановки

Алгоритм решения системы двух линейных уравнений методом подстановки. Выполнение упражнений

Алгоритм решения системы двух линейных уравнений методом подстановки. Выполнение упражнений

Решение систем линейных уравнений методом сложения. Алгоритм решения систем уравнений методом сложения

Закрепить навык решения системах двух линейных уравнений методом сложения.

Формировать умение объективно оценивать свой труд.

Развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

Алгоритм решения системы двух линейных уравнений с двумя переменными методом сложения. Применение алгоритма к решению систем ур.авнений

Алгоритм решения системы двух линейных уравнений с двумя переменными методом сложения. Выполнение упражнений

Решение систем линейных уравнений методом сложения. Выполнение упражнений

Решение систем двух линейных уравнений методом сложения. Выполнение упражнений

Решение задач с помощью систем линейных уравнений. Составление математических моделей реальных ситуаций с помощью систем двух линейных уравнений с двумя переменными

Обобщить и систематизировать навык решения задач, в которых используют системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций.

Формировать интерес к изучению темы и желание применять приобретенные знания и умения.

Формировать умение использовать приобретенные знания в практической деятельности.

Решение задач с помощью систем линейных уравнений. Составление математических моделей реальных ситуаций с помощью систем двух линейных уравнений с двумя переменными

Решение задач на движение с помощью систем линейных уравнений. Решение задач

Решение задач на проценты и части с помощью систем линейных уравнений. Решение задач

Решение задач разного типа с помощью систем линейных уравнений. Решение задач

Повторение и систематизация учебного материала

Контрольная работа № 7 по теме «Системы линейных уравнений с двумя переменными»

Повторение и систематизация учебного материала (8 ч.)

Анализ контрольной работы. Свойства степени с натуральным показателем. Выполнение упражнений

Обобщить и систематизировать учебный материал за курс 7 класса

Формировать интерес к изучению алгебры

Формировать умение использовать приобретенные знания в практической деятельности

Формулы сокращенного умножения. Выполнение упражнений

Функции. Выполнение упражнений

Решение систем линейных уравнений. Выполнение упражнений

Решение задач с помощью систем линейных уравнений. Выполнение упражнений

Подготовка к контрольной работе

Итоговая контрольная работа № 8

Итоговая контрольная работа № 8

VI. Реализация национальных, региональных и этнокультурных особенностей

№ п/п	Содержание учебного материала, учитывающего национальные, региональные и этнокультурные особенности
	Бассейн реки Урал представлен рекой Урал и притоками. Основные реки бассейна реки Урал текут в широтном направлении, берут начало с восточных склонов Уральских гор. Этот бассейн охватывает площадь 16,4 тыс. км2 (18,5 % площади области). Какова площадь области?
	Река Ай берет начало в 40 км от г. Златоуста. Река, протекая по территории Челябинской области и Республики Башкортостан, впадает в р. Уфу. На территорию Челябинской области приходится 242 км из общей протяженности реки 552 км. Какой процент протяженности находится в Челябинской области?
	Лыжник от озера Смолино до деревни Зуевка шел со скоростью 15 км\ч, а обратно - со скоростью 12км\ч. Сколько времени ушло у него на обратную дорогу, если на весь путь туда и обратно лыжник затратил 3 ч.?
	На диаграмме показана среднемесячная температура воздуха в Челябинске за каждый месяц 2010 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 2010 году. Ответ дайте в градусах.
	Задача на повторение Набор ручек в Челябинской фирме «Комус» стоит 80 рублей, продается с 25%-й скидкой. При покупке 4 таких наборов покупатель отдал кассиру 500 рублей. Сколько рублей сдачи он должен получить?
	Задание для устной работы на уроке. Поезд Челябинск-Адлер отправляется в 13 ч. 20 мин., а прибывает в 4 ч. 21 мин. Он идет 2 дня 15 часов. Сколько времени (в часах) он находится в пути?
	Задача на повторение. Книга «Челябинск: двенадцать историй о любимом городе» челябинского историка-краеведа Владимира Боже поможет совершить путешествие из прошлого в настоящее Челябинска. Каждая история посвящена определенной странице из жизни мегаполиса. Всего страниц в книге 272, причем текст занимает места в 16 раз больше, чем фотографии. Сколько страниц занимает текст этой книги и сколько фотографии?
	Найдите сумму многочленов и вычислите значение полученного выражения при х=4, у=1: (3х2+200у+10)+(105х2-25у-6). В ответе вы получите число, которое является годом основания города Копейск Челябинской области.
	В Челябинской фирме «Альтерм» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле С=6500+4000n, где n – число колец, установленных при рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 12 колец.
	Стиральная машина в торговом комплексе «Эльдорадо» г.Челябинска, которая стоила 4500 рублей, продается с 10%-ой скидкой. При покупке этой машины покупатель отдал кассиру 5000 рублей. Сколько рублей сдачи он должен получить?
	Разложите разность квадратов на множители и вычислите значение выражения при х=5, у=7. Получите число животных, занесенных в красную книгу Челябинской области: 9х2-у2
	Паде́ние метеори́та Челя́бинск — столкновение с земной поверхностью фрагментов небольшого астероида, разрушившегося в результате торможения в атмосфере Земли 15 февраля 2013 года примерно в 9 часов 20 минут по местному времени. Суперболид взорвался в окрестностях Челябинска на высоте 15-25 км. Первые осколки, в виде небольших метеоритов, были найдены несколькими днями позже. При последующих поисках в озере Чебаркуль был обнаружен самый крупный осколок весом 570 кг и множество более мелких осколков суммарным весом несколько килограммов. Сложите все числа данного текста, из полученного результата вычтите число 1054. Получится число, равное количеству пострадавших в результате этого события.
	Двое рабочих Челябинского кузнечно-прессового завода изготовили по одинаковому количеству деталей. Первый выполнил эту работу за 5ч, а второй за 4ч, так как изготовлял в час на 12 деталей больше первого. Сколько деталей изготовил каждый рабочий?
	В Челябинской городской думе заседало 60 депутатов, представляющие две партии. После выборов число депутатов от первой партии увеличилось на 12%, а от второй партии – уменьшилось на 20%. Сколько депутатов от каждой партии оказалось в городской думе после выборов, если всего было выбрано 56 депутатов?
	У меня в холодильнике в общей сложности 19 куриных и  перепелиных яиц производства птицефабрики «Чебаркульская птица». После приготовления яичницы из 2 куриных и  5 перепелиных яиц, перепелиных стало в два раза больше, чем куриных.  Сколько куриных яиц было в холодильнике изначально?

38