Республика Саха (Якутия)
Верхоянский район
МБОУ «Батагайская средняя общеобразовательная школа»
«Задача гениального Гаусса»
Авторы:
ученики 4 «а» класса
Акимова Амалия,
Стручкова Валя
Руководитель:
Ефимова Т.Е.
2016г.
Математика - царица наук. Математика неисчерпаема и многозначна. Одних покоряет её логическая стройность, другие ценят в ней точность, a третьи восхищаются её красотой.

Цель проекта: знакомство с жизнью и деятельностью Карла Фридриха Гаусса, научиться решать задачи, пользуясь способом Гаусса.
Задачи проекта:
найти интересные сведения о его жизни используя различные источники;
уяснить, что подсчет суммы последовательных чисел можно провести через группировку чисел в пары.
Юный Карл Фридрих, по его собственным словам, «научился считать раньше, чем говорить». Рассказывают, когда отец однажды громко подсчитывал заработок своих помощников, трехлетний Карл на слух заметил ошибку в вычислениях и указал на нее отцу.
В 1784 году семилетний Карл начинает учиться в местной однокомплектной (то есть с одним учителем) школе. Первый биограф Гаусса, профессор фон Вальтерсгаузен пишет: «...Душная комната с низким потолком и неровным, потрескавшимся полом. Из одного окна открывается вид на готические башни церкви св. Катарины, из другого — на конюшни. Среди сотни учеников от семи до пятнадцатилетнего возраста взад и вперед расхаживает учитель Бюттнер с хлыстом в руках. Этим беспощадным аргументом своего метода воспитания учитель пользовался достаточно часто — по настроению и по потребности. В этой школе, как бы вырванной из далекого средневековья, юный Гаусс проучился без особых происшествий два года, а затем был переведен в «арифметический класс». Впрочем, «перевод» выразился лишь в том, что девятилетнего мальчика пересадили из одного ряда скамеек в другой. Ученикам, сидевшим в этом ряду, тот же учитель Бюттнер давал меньше заданий по правописанию и больше — по арифметике. Ученик, первым выполнивший заданное вычисление, клал обычно свою грифельную доску на большой стол; поверх нее клал доску второй, и так далее по порядку. Затем кипа досок переворачивалась. Учитель начинал проверку с доски того, кто решил первым.
Вскоре после перевода девятилетнего Гаусса в арифметический класс учитель дал задание: сложить все натуральные числа от 1 до 100. «Едва задание было сформулировано,— продолжает фон Вальтерсгаузен,— как юный Карл объявил: «Я положил свою доску». И пока остальные школьники прилежно складывали и перемножали числа, учитель Бюттнер, исполненный собственного достоинства, расхаживал по классу, бросая время от времени саркастические взгляды на младшего из учеников, который давно выполнил задание. А тот спокойно улыбался, проникнутый непоколебимой уверенностью в правильности полученного результата — эта уверенность овладевала Гауссом после окончания каждой крупной работы в течение всей его жизни... В конце урока на грифельной доске Гаусса обнаружилось единственное число, которое, к общему изумлению, представляло собой правильный ответ на поставленную задачу, тогда как многие другие ответы оказались неверными и подлежали «исправлению с помощью хлыста».
«Вместо того, чтобы складывать последовательно 1+2=3; 3+3=6; 6+4=10; 10+5=15 и т.д., что было бы естественным для любого нормального школьника такого возраста, Гауссу пришло в голову объединить попарно числа с разных концов данного ряда: 1+100=101; 2+99 = 101 и т.д. Таких пар оказалось 50. Затем оставалось лишь выполнить умножение 101х50=5050. Нечего и удивляться: Гауссу не понадобилось много времени, чтобы написать на своей доске это единственное число».
Бюттнер обратил внимание на незаурядные способности своего ученика и достал для него дополнительные пособия. Большую помощь оказал молодой помощник учителя Мартин Бартельс, который также был неравнодушен к математике. Несмотря на восьмилетнюю разницу в возрасте, Гаусс и Бартельс быстро сблизились на почве общего увлечения математикой. Бюттнер и Бартельс убедили отца Гаусса направить сына в гимназию и обещали добиться материальной поддержки: у бедного ремесленника не было возможности платить за обучение сына в гимназии.
В 1788 году Гаусс был принят — небывалый случай! — сразу во второй класс гимназии. Особенно поразил он своих педагогов блестящими способностями к греческому языку и латыни — эти древние языки наряду с историей считались важнейшими в гуманитарном гимназическом образовании. В те времена дети крестьян и ремесленников весьма редко попадали в гимназии и тем более в университеты — образование и получение «привилегированных» профессий было практически недоступно для низших классов общества. Гаусс оказался счастливым исключением.
Чтобы понять, как рассуждал Гаусс, разберем задачу – найдем сумму всех натуральных чисел от 1 до 10.
1.Найти сумму 1 + 2 +3 +4 +5 +6 +7 +8 + 9+10.
Объединим слагаемые в пары – первое с десятым, второе с девятым и т.д. Всего у нас 5 таких пар и каждая пара в сумме дает 11.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 = (10 +1) 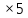 = 55
= 55
Ответ: 55
2. Найти сумму 1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 +11 + 12 +13 + 14
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 +11 + 12 +13 + 14= (1 + 14) 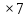 =85
=85
Ответ: 85
3. Найти сумму чисел 1 + 2 +3 +4 +5 +6 +7 +8 + 9.
(1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8 + 9 +10) – 10 = 55 – 10 =45
Ответ: 45
А теперь перейдем к задаче маленького Гаусса.
4. Найти сумму чисел от 1 до 100.
1 + 2 + 3 + …+ 98 + 99 + 100.
1 + 2 + 3 + … + 98 + 99 + 100 = (1 + 100) 50 = 5050.
Ответ: 5050.
5. Найти сумму чисел от 1 до 1000.
1 + 2 + 3 + … + 998 + 999 + 1000 = (1 + 1000) ×500 = 500 500.
Ответ: 500 500
6. Найти сумму чисел от 1 до 220.
1 + 2 + 3 + … + 218 +219 + 220 = (1 +220) ×110 = 24 310
Ответ: 24 310
7. Найти сумму чисел от 1 до 221.
(1 + 2 + 3 + … + 218 +219 + 220) + 221 = (1 +220) ×110 + 221= 24 310 + 221 = 24 531
8. Имеется 9 гирь весом 1 г, 2 г, 3 г, 4 г, 5 г, 6 г, 7 г, 8 г, 9 г. Можно ли разложить их на три кучки с равным весом?
Решение.
Найдем сумму гирь методом Гаусса:
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
Сумма масс всех гирек 45 г. Значит, в одной кучке будут гири весом 15г. Попробуем это сделать: 1 г + 9 г + 5 г, 2 г + 6 г + 7 г, 3 г + 4 г + 8 г. Здесь возможны и другие результаты, например: 1 г + 8 г + 6 г, 3 г + 5 г + 7 г, 2 г + 4 г + 9 г.
9. Можете ли вы разделить циферблат часов прямой линией на 2 равные половины так, чтобы суммы чисел на каждой половине были равны?
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78 – сумма чисел от 1 до 12.
Нужно, чтобы в каждой части было 78 :2 = 39.
Проведем линию между 9 и 10, между 3 и 4.


Проверка: (10 + 3) ×3 = 39 и (9 + 4) × 3=39
10. Проведите на циферблате часов две прямые линии, чтобы в каждой части сумма чисел была одинакова.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78 – сумма чисел от 1 до 12.
Нужно, чтобы в каждой части было 78 : 3 = 26.
Проведем линии между а) 10; 11 и 2, 3; б) 8; 9 и 4; 5.
1 + 2 +3 +4 +5 +6 +7 +8 + 9+10



Остроумный ответ Гаусса
Из биографии Гаусса известно, что еще в народной школе он поражал учителя Бюттнера своим умом и остроумием. Однажды учитель спросил ученика: «Карл, я сейчас задам тебе два вопроса. Если на первый ты ответишь правильно, то на второй можешь не отвечать. Итак, скажи мне, сколько иголок на рождественской елке?». Карл без промедления ответил: «67 534». «Как ты так быстро сосчитал иголки?» – изумился учитель. «А это уже второй вопрос, господин учитель», – улыбнулся ученик.

11. Летит стая птиц. Впереди одна птица(вожак), за ней две, потом три, четыре и т.д. Сколько птиц в стае, если в последнем ряду их 20?
Решение: 1 + 2 +3 +4 +5 +6 + … + 18 +19 + 20 = (1 + 20) ×10 = 210
Ответ: 210.

12. Как рассадить 45 кроликов в 9 клетках так, чтобы во всех клетках было разное количество кроликов?
1 + 2 +3 +4 +5 +6 +7 +8 + 9 = (1 + 2 +3 +4 +5 +6 +7 +8) + 9 = (1 + 8) 4 + 9 = 45
Всего 9 слагаемых, значит, в первую –1, во вторую –2, …, в девятую-9.
Ответ: В первую –1, во вторую –2, …, в девятую-9.
13.Набор состоит из 12 гирек массой 1г,2г,…,12г из набора убрали 4 гирек, общая масса которых равна трети общей массы всех гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Вес всех гирь равен1 + 2 +3 +4 +5 +6 +7 +8 + 9+10 + 11 + 12 = (1 + 12) × 6= 78
Ее третья часть 78 : 3 = 26
Разобьем все гири на пары 1-12, 2-11, 3-10, 4-9, 5-8, 6-7. 4 9
211
1 12
6 7
5 8
3 10
Если мы уберем 4 гири весом 26 грамм, то при этом мы «разобьем» самое большее четыре пары, а две пары останутся точно нетронутыми, которые составляют тоже треть общей массы.
Таким образом. Мы получили первую четверку убранную, вторую четверку гарантированно оставшуюся (две пары) и третью четверку нетронутую, которая тоже будет весом 26 грамм.
Ответ: Можно.
Вывод:
Работая над этой темой, мы узнали, то в конце 18 века родился великий математик Карл Фридрих Гаусс. Благодаря его трудам, у нас появилась возможность без труда найти ответ в тех задачах, которые на первый взгляд трудно решить или можно потратить очень много времени. Благодаря изучения его жизни и наследия его трудов, мы лишний раз убеждаемся в величие и возможностях человеческого ума.
Литература:
1. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
2. Интернет – ресурсы.

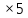 = 55
= 55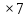 =85
=85






















