Золотая пропорция в математике

Цель урока:

• познакомить учащихся с понятием “золотое сечение”;

• закрепить навык решения уравнений, используя основное свойство пропорции;

• расширить кругозор и активизировать познавательную деятельность учащихся;

• вовлечь учащихся в исследовательскую деятельность.

Ход урока

Урок сопровождается презентацией.

I. Вступительное слово учителя.

С древних времен человек начал разделять вещи как красивые и не красивые. Уже в Древней Греции античные философы начали выявлять некую формулу, которая раскрыла тайну того, что мы называем гармонией. Так что же такое гармония?

Вопросы к классу: “Ребята! Как, вы, считаете, что же такое гармония? С какими словами у вас ассоциируется слово “гармония”?

Обобщаем ответы учащихся (Слайд 1):

Если рассматривать цветок вблизи и аналогично другие естественные и созданные человеком творения, то можно найти единство и порядок, свойственные всем этим предметам. Этот порядок и единство и есть Гармония, определяющая Красоту.

Итак, гармония, - это красота, а красота, как говорили греки, - это математика. Следовательно, гармония, - это математика.

Из многих пропорций, которыми пользовался человек при создании живописи, скульптуры, музыки, поэм, самой главной является одна, и именно она отражает понятие ГАРМОНИИ наилучшим образом. Эту пропорцию называли по-разному: божественной, золотой, золотым сечением, золотой серединой, золотым делением, золотым числом. (Слайд 2)

Мы назовем ее с вами “Золотое сечение”

Иоганн Кеплер говорил: “Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением. И если первое из этих двух сокровищ можно сравнить с мерой золота, то второе с драгоценным камнем”.

Чтобы найти этот драгоценный камень я предлагаю вам отправиться в экспедицию.

II. Экспедиция.

У каждого учащегося на столе лежат маршрутные листы (Приложение 1)

Для любого путешествия необходимо собрать багаж. Давайте пополним наш багаж знаний определением. Для этого мы отправляемся на станцию “Теоретическая”.

ТЕОРЕТИЧЕСКАЯ. (Слайд 2)

Золотым сечением называют деление отрезка, при котором длина его большей части так относится к длине всего отрезка, как длина меньшей части к большей.

АВ : АС = ВС : АВ

Это отношение приближённо равно 0,618 или 

Итак, багаж упакован, можно отправляться в экспедицию.

ВИТРУВИЙ (Слайд 3)

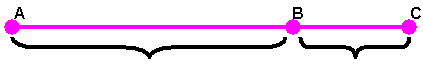
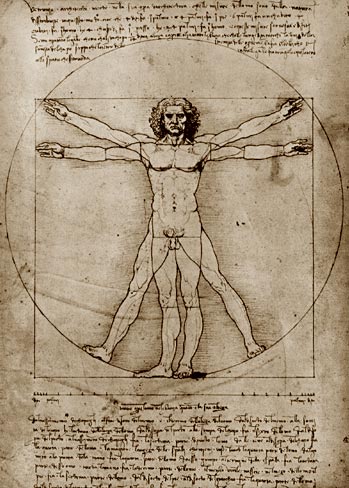П еред вами Витрувианский человек — рисунок, нарисованный Леонардо Да Винчи примерно в 1490-92 годах как иллюстрация для книги, посвящённой трудам античного римского архитектора Витрувия, Рисунок является одновременно научным трудом и произведением искусства, также он служит примером интереса Леонардо к пропорциям. В соответствии с сопроводительными записями Леонардо, он был создан для определения пропорций (мужского) человеческого тела.

Термин "золотое сечение" был введён именно Леонардо да Винчи, который использовал золотое сечение как пропорции "идеального человеческого тела".

Известно, что анатомическая особенность человека описывается золотым сечением. Например: если мы измерим расстояние от локтя до кончиков пальцев и разделим получившийся результат на расстояние от плеча до кончиков пальцев, то получим отношение  !

ЗАДАЧА 1 (Слайд 3, 4)

• Расстояние от локтя до кончиков пальцев у человека равно 40 см. Найдите расстояние от плеча до кончиков пальцев этого человека.

ЗАДАЧА 2 (Слайд 5)

• Рост человека 160 см. На какой высоте от пола должна находиться его талия, чтобы делить тело в отношении золотого сечения, т. е.  ?

Д НК. (Слайд 6)

Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Отношение ширины спирали к её длине составляет приблизительно  .

ЗАДАЧА 3.

• Известно, что длина спирали 34 ангстрема, найдите ширину спирали. (1 ангстрем = 0,0000001 мм)

ПОДСОЛНУХ. (Слайд 7)

У дивительно, что семена подсолнуха располагаются по спирали, против часовой стрелки, и отношение последующего диаметра спирали к предыдущему равно  !

ЗАДАЧА 4. (Слайд 8)

• Диаметр одной спирали семян подсолнечника равен 2см. Найдите диаметр предыдущей спирали.

ЗООЛОГИЧЕСКАЯ. (Слайд 9)

Головоногий моллюск наутилус также подчиняется божественной пропорции, т.е. соотношение диаметра каждого витка спирали к последующему равно  !

ЗАДАЧА 5 (Слайд 10)

• Первый виток спирали равен 1.2см. Найдите размер второго витка спирали.

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как  !

ЗАДАЧА 6 (Слайд 11)

• Найдите длину всей ящерицы, если длина её хвоста 16 см.

ПАРФЕНОН. (Слайд 12)

П арфенон – один из самых величественных храмов Древней Греции. Отношение высоты здания к его длине равно  !

ЗАДАЧА 7 (Слайд 13)

• Длина Парфенона 69,54 м. Найдите высоту храма, если его высота относится к длине по правилу “золотого сечения”, т.е. в отношении 5/8.

М УЗЫКАЛЬНАЯ. (Слайд 14)

Любая скрипка сделана по закону золотого сечения. Длина её части грифа относится к длине деки, как 5/8!

ЗАДАЧА 8 (Слайд 14)

• Найдите длину скрипки, если длина деки 36 см.

III. Подведем итоги нашей экспедиции. (Слайд 15)

Странная, загадочная, необъяснимая вещь: эта божественная пропорция мистическим образом сопутствует всему живому.

Неживая природа не знает, что такое “золотое сечение”. Но вы непременно увидите эту пропорцию и в изгибах морских раковин, и в форме цветов, и в облике жуков, и в красивом человеческом теле.

Все живое и все красивое — все подчиняется божественному закону, имя которому — “золотое сечение”.

Так что же такое “золотое сечение”? Что это за идеальное, божественное сочетание?

Может быть, это закон красоты?

Или все-таки он — мистическая тайна?

Научный феномен или этический принцип?

Ответ неизвестен до сих пор. Точнее — нет, известен. “Золотое сечение” — это и то, и другое, и третье. Только не по отдельности, а одновременно... И в этом его подлинная загадка, его великая тайна. Так считал Анхель де Куатьэ

IV. Домашнее задание.

Найти примеры “золотого сечения” в природе, архитектуре, живописи и т. д. и составить задачи. Материал желательно оформить в виде презентации.

Примечание: во время решения задач учащиеся могут работать в парах или группах.