Дополнительный материал к уроку
Интернет-ресурсы: https://ru.wikipedia.org/, http://ilibrary.ru/, http://tut-interesno.org/, http://ifaq.su/
Софизмами называют рассуждения, специально созданные для того, чтобы ввести людей в заблуждение. Бывало и так, что сам философ не мог понять, где в его рассуждениях ошибка. Подобные высказывания называются апориями. Разгадывать софизмы и апории — одно из увлекательных занятий для пытливого ума, нечто вроде попытки разгадать секрет фокуса иллюзиониста, не говоря уже о том, что подобная тренировка ума, делает человека более бдительным и менее подверженным обману, потому что за поверхностной красивостью и убедительностью слов ему становится легче разгадать ошибку.
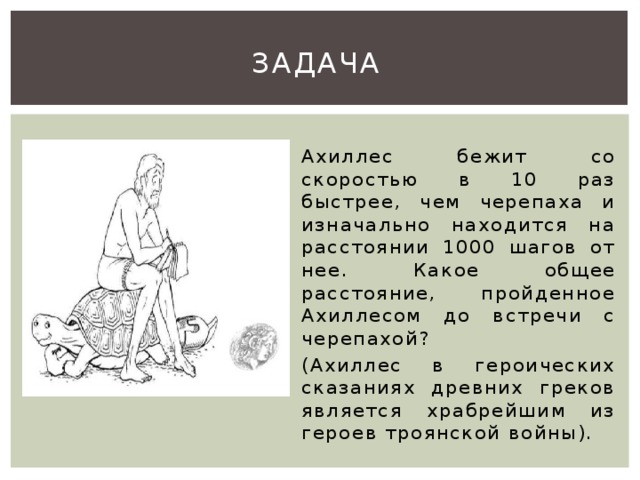
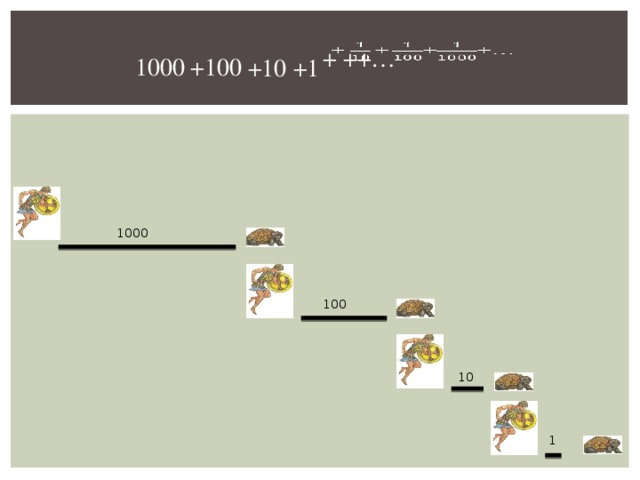
Попробуем разгадать одну из самых известных апорий Зенона — парадокс Ахиллеса и черепахи. Итак, вот рассуждения Зенона: допустим, Ахиллес бежит в десять раз быстрее, чем черепаха, и находится позади неё на расстоянии в тысячу шагов. За то время, за которое Ахиллес пробежит это расстояние, черепаха в ту же сторону проползёт сто шагов. Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Есть один небольшой момент, о котором Зенон не знал, а древнегреческие математики, такие как Архимед, только догадывались. А конкретно, они не знали, что делать с бесконечностью. Древние греки вообще её побаивались и старались избегать, а более-менее окончательно с ней разобрались только к восемнадцатому веку, когда был создан математический анализ. Поэтому нет ничего удивительного в том, что когда речь заходила о бесконечности, древние философы начинали пасовать перед ней: у них просто не было достаточно глубоких знаний в математике, чтобы разрешить кажущиеся противоречия.
Попробуем разобраться, в чём же тут дело с высоты сегодняшних знаний. Во-первых, сразу бросается в глаза тот факт, что на каждом этапе время, затрачиваемое Ахиллесом, чтобы пробежать разделяющее его и черепаху расстояние, резко уменьшается. Через несколько этапов оно становится совсем крохотным, практически незаметным, точно также практически незаметным становится расстояние, разделяющее Архимеда и черепаху. Если вначале оно было равно тысяче шагов, то уже через 5 этапов оно будет равно всего одной сотой шага. Есть один тонкий момент, который может быть трудно преодолеть человеку, который до этого мало задумывался о бесконечности: когда мы складываем бесконечное количество таких вот быстро уменьшающихся кусочков, то результат может быть конечным. Покажем это на примере. Возьмём кусок масла и будем отрезать от него кусочки. Допустим, мы сначала отрежем половину, потом половину от оставшейся половины и т.д. Ясно, что кусок масла не является бесконечно делимым. Очень скоро, мы дойдём до размеров молекул и дальше уже делить не сможем, но что нам стоит представить себе, что никаких молекул нет и мы можем делить масло бесконечно? Что мы тогда получим? Мы сможем бесконечно отрезать половину от кусочка масла и получим таким образом бесконечное количество кусочков, но общее количество отрезанного масла никогда не будет больше количества того масла, что было у нас изначально. Другой пример: нарисуем две параллельные линии на бумаге, теперь между ними нарисуем ещё одну линию, между второй и третьей — ещё одну и т.д. Если бы у нас была бесконечно тонкая ручка, мы могли бы продолжать этот процесс бесконечно, получая бесконечное количество промежутков между линиями, но суммарное расстояние между этими линиями не будет превышать расстояния между первыми двумя прямыми, которые мы нарисовали…
Один из «парадоксов древнегреческого философа Зенона» состоит в следующем в изложении Льва Толстого в «Войне и мире» (т. 3, ч. 3): Для человеческого ума непонятна абсолютная непрерывность движения. Человеку становятся понятны законы какого бы то ни было движения только тогда, когда он рассматривает произвольно взятые единицы этого движения. Но вместе с тем из этого-то произвольного деления непрерывного движения на прерывные единицы проистекает большая часть человеческих заблуждений.
Известен так называемый софизм древних, состоящий в том, что Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идет в десять раз скорее черепахи: как только Ахиллес пройдет пространство, отделяющее его от черепахи, черепаха пройдет впереди его одну десятую этого пространства; Ахиллес пройдет эту десятую, черепаха пройдет одну сотую и т. д. до бесконечности. Задача эта представлялась древним неразрешимою. Бессмысленность решения (что Ахиллес никогда не догонит черепаху) вытекала из того только, что произвольно были допущены прерывные единицы движения, тогда как движение и Ахиллеса и черепахи совершалось непрерывно.
Принимая все более и более мелкие единицы движения, мы только приближаемся к решению вопроса, но никогда не достигаем его. Только допустив бесконечно-малую величину и восходящую от нее прогрессию до одной десятой и взяв сумму этой геометрической прогрессии, мы достигаем решения вопроса. Новая отрасль математики, достигнув искусства обращаться с бесконечно-малыми величинами, и в других более сложных вопросах движения дает теперь ответы на вопросы, казавшиеся неразрешимыми.
Эта новая, неизвестная древним, отрасль математики, при рассмотрении вопросов движения, допуская бесконечно-малые величины, то есть такие, при которых восстановляется главное условие движения (абсолютная непрерывность), тем самым исправляет ту неизбежную ошибку, которую ум человеческий не может не делать, рассматривая вместо непрерывного движения отдельные единицы движения.
В отыскании законов исторического движения происходит совершенно то же.
Движение человечества, вытекая из бесчисленного количества людских произволов, совершается непрерывно. Для изучения законов истории мы должны изменить совершенно предмет наблюдения, оставить в покое царей, министров и генералов, а изучать однородные, бесконечно-малые элементы, которые руководят массами.
.
+ 
+…
.
.
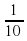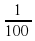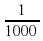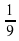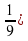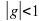
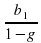
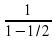=2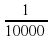
,…
·
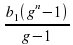
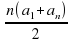
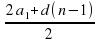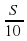, и расстояние между ними уменьшится на 
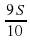. Если в начале оно равнялось 1000 шагам, а в момент встречи стало нулевым, то 
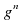бесконечно мало, и им можно пренебречь. Тогда 
, 
=
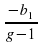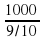