Класс: 11
Тип урока: урок применения знаний и умений учащихся.
Форма урока: урок-практикум.
УМК: Атанасян Л.С., Геометрия 10-11.
Цель урока: развивать у учащихся навыки применения теоретических знаний по теме «Объём конуса» для решения задач практической направленности.
Задачи:
1.совершенствовать умения учащихся применять накопленные знания в измененной ситуации, делать выводы и обобщения; показать практическую значимость данной темы в жизни человека.
2.способствовать формированию у учащихся ключевых компетенций (сравнение, сопоставление, классификация объектов, определение адекватных способов решения учебной задачи на основе заданных алгоритмов); развитию памяти, внимания, мышления и пространственного воображения учащихся, навыков самооценки и самоконтроля; навыков творческого подхода к решению задач, исследовательской работы над задачей.
3.способствовать развитию устойчивого интереса и созданию положительной внутренней мотивации к изучению математики; воспитанию ответственного отношения к учению.
Технологии: личностно-ориентированная, проблемно-исследовательская, индивидуально–дифференцированного обучения, ИКТ.
Методы обучения: словесный, наглядный, практический, частично-поисковый, проблемный.
Формы работы: индивидуальная, фронтальная, групповая.
Оборудование и материалы для урока: компьютер, проектор, экран, презентация к уроку (Приложение №1), карточки для работы в группах , дифференцированное домашнее задание, отрывок из трагедии А.С.Пушкина «Скупой рыцарь», физкультминутка, оценочные листы.
Место урока в теме, разделе: тема «Объём конуса» включена в раздел «Объёмы тел». На изучение темы отводится 2 часа, данный урок первый.
Продолжительность урока – 45 мин.
Структура урока
I. Организационный момент.
II.Проверка домашнего задания .
III. Актуализация знаний учащихся.
IV. Сообщение темы, цели урока, мотивация учебной деятельности.
V. Применение знаний и умений учащихся в измененной и новой ситуациях (решение практикоориентированных и проблемных задач).
а) Решение практикоориентированных задач.
б) Решение проблемной (исторической) задачи.
VI. Физкультминутка – 1 мин.
VII. Дополнительная информация о конусе «Это интересно».
VIII. Дифференцированное домашнее задание.
IX. Подведение итога урока. Рефлексия.
X. Оценки за урок.
Конспект урока
Презентация к уроку (Приложение №1)
I.Организационный момент – 2 мин.
-Учитель приветствует учащихся. Отмечает отсутствующих и предлагает отгадать ребус. Отгадать тело вращения, объем которого будем изучать.(Слайд 1)
II.Проверка домашнего задания – 4 мин.
- Назовите известные вам тела вращения. Вспомните формулы объёмов изученных тел вращения. Эти формулы вам потребуются для решения задач ЕГЭ, поэтому их нужно знать.
Из деревянного цилиндра, высота которого равна диаметру основания, выточен наибольший шар. Сколько процентов материала сточено?
- У кого есть замечания по решению задачи? У кого есть дополнения?
III. Актуализация знаний учащихся (Слайд 2).
-Задачи на вычисление объёмов геометрических тел интересовали учёных – математиков ещё с древности. В своей работе «О шаре и цилиндре» Архимед доказал, что отношение объемов шара и описанного около него цилиндра равно 2:3. Этим открытием он так дорожил, что в завещании просил поставить на своей могиле памятник с изображением цилиндра с вписанным в него шаром и надписью расчета, благодаря чему через 200 лет была найдена могила Архимеда. Сегодня вы решили знаменитую задачу Архимеда и соприкоснулись с историей математики.
VI. Сообщение темы, цели урока, мотивация учебной деятельности -2 мин. (Слайд 3)
- Сегодня мы отправимся в увлекательный мир геометрии, который вам откроет некоторые тайны, связанные с телами вращения, ведь геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли.
Тема нашего урока: «Объём конуса».
Цель урока: учиться применять теоретические знания по теме «Объём конуса» для решения практических задач.
Мне хочется, чтобы вы ещё раз убедились, что математика интересная и увлекательная наука, тесно связанная с жизнью и окружающим миром.
Ведь недаром ещё Аристотель говорил, что ум заключается не только в знании, но и в умении применять знания на практике.
Трудно назвать чаще встречающиеся задачи на практике, чем задачи на вычисление объёмов. О них задумываются и строя дома, и переливая воду из одного сосуда в другой.
Как Вы думаете, какова связь между этим телом и этой картиной? (Слайд 4).
Оказывается, самая непосредственная…(Слайд 5)
Археологические раскопки доказывают, что с конусами люди были знакомы с древних времён. (Слайд 6) Например, в Древней Греции время, отводимое для речей, измеряли с помощью водяных часов. Старинные египетские водяные часы (клепсидра) представляли собой сосуд, имеющий форму конуса, наполненный водой, которая вытекала через отверстие в нижней его части. Уровень воды показывал время, истекшее с момента наполнения сосуда.
С тех времен дошли до нас выражения «Много воды утекло», «Как медленно течет время».
- Как вы думаете, нужны ли нам в жизни конусы?
- Конусы окружают нас повсюду: в природе (Слайд 7), в архитектуре (Слайд 8), технике и на производстве (Слайд 9), т.е., находят свое применение во всех сферах человеческой деятельности.
Конические детали имеются во многих машинах и механизмах: в автомобилях, танках. Носовая часть самолетов и ракет также имеет коническую форму. Чаще всего конусы используют в совокупности с другими телами или друг с другом.
- Подумайте, для чего важно уметь решать задачи на вычисление объёмов конуса и других тел?
Тема «Объёмы тел вращения» ещё важна тем, что она включена в задания ЕГЭ.
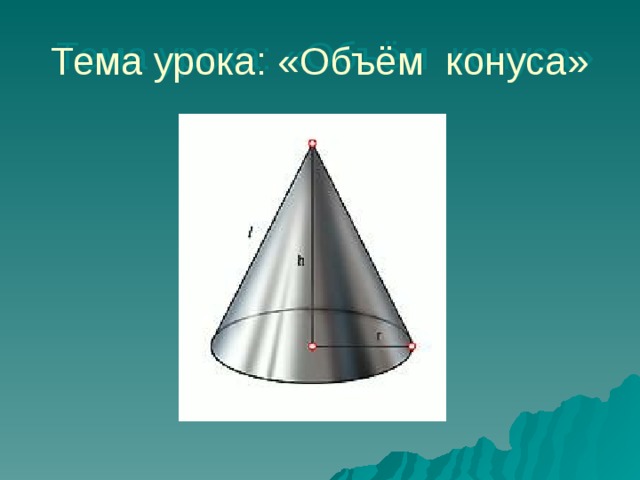
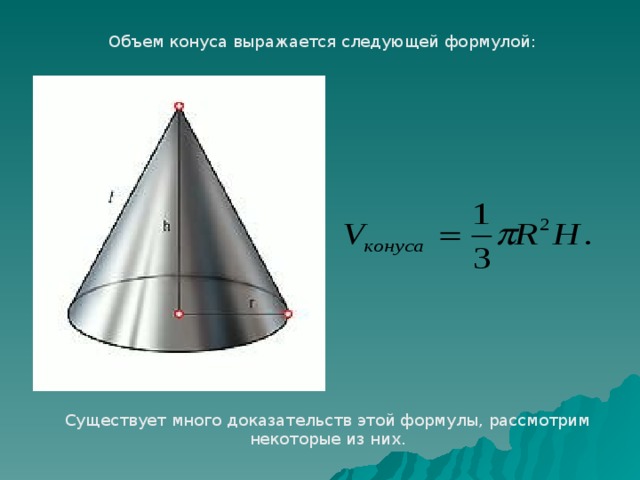
Ну, а теперь познакомимся с формулой позволяющей нам рассчитать объем конуса (Слайд 10) и рассмотрим доказательство теоремы (Слайд 11)
V. Применение знаний и умений учащихся в измененной и новой ситуациях (решение практикоориентированных и проблемных задач) -17 мин.
Сегодня на уроке будут работать группы. Каждая группа (1 группа и 2 группа) имеет своего консультанта. Консультант оценивает работу каждого члена группы (группа 2 более сильная)
У фермера 3 коровы. Для содержания одной коровы фермеру требуется заготовить на зиму 3 т сена. Он заготовил стог сена в виде конуса с радиусом основания 6 м и образующей 10 м. Определите массу заготовленного сена при плотности 30кг/м3 .Хватит ли коровам сена на зиму?
Авиационная бомба среднего калибра дает при взрыве воронку диаметром 6 м и глубиной 2 м. Найдите массу земли, выбрасываемую бомбой, если плотность земли 1650 кг /м3.
Послушайте легенду восточных народов, рассказанную А.С. Пушкиным в трагедии «Скупой рыцарь»
«…Читал я где-то,
Что царь однажды воинам своим
Велел снести земли по горсти в кучу,-
И гордый холм возвысился,
И царь мог с вышины с весельем озирать
И дол, покрытый белыми шатрами,
И море, где бежали корабли…»
-Представьте иллюстрацию к отрывку.
Перед нами встала проблема: «Прав ли был А.С. Пушкин, назвав получившийся холм «гордым»?»
VI. Физкультминутка
Разгрузка зрительных анализаторов.
Почти 90% всей информации человек воспринимает глазами. Если устают глаза, снижается наше внимание и активность. Давайте перед следующим заданием дадим отдых глазам и себе.
1. Закройте глаза на несколько секунд, сильно напрягая глазные мышцы, затем раскройте их, расслабив мышцы. Повторите 3-4 раза.
2. Посмотрите на переносицу и задержите взор. Затем посмотрите вдаль. Повторите 3-4 раза.
3. Медленно наклоняйте голову: вперед- влево- вправо- назад. Повторите 3-4 раза.
VII. Решение проблемной (исторической) задачи (работают группы)
Подведем итоги решения задач. Если первая и вторая задачи не вызвали затруднений, то третья задача поставила вас в тупик. Давайте вместе решим задачу
- Переведём задачу на язык геометрии.
- Холм – это конус. Но какого объёма?
- Достаточно ли данных в задаче?
- Что нужно знать, чтобы найти высоту?
- Чтобы разобраться в поставленной задаче, надо составить её математическую модель и наметить этапы решения.
Пусть 1горсть≈ литра=0,2 дм3
литра=0,2 дм3
n =100000 (В древности войско в 100000 воинов считалось очень внушительным).
α=45° (Возьмем угол наклона образующей к плоскости основания конуса равным 45°. Взяв больший угол наклона, земля начнет осыпаться).
(Учащиеся в группах намечают этапы решения и обсуждают решение задачи)
Vк = 0,2∙100000 = 20000дм3 = 20м3. 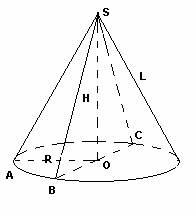
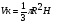
Так как H = R, то
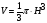 ,
, 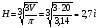
(Группы защищают своё решение)
- Легенда звучит правдоподобно, но вы смогли доказать, что А.С. Пушкин был неправ, назвав холм «гордым». Надо обладать очень богатым воображением, чтобы земляную кучу в 2,7 м (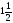 человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, вы получили бы еще более скромный результат. Таким образом, математика помогает критически относиться к художественным произведениям.
человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, вы получили бы еще более скромный результат. Таким образом, математика помогает критически относиться к художественным произведениям.
VII. Дополнительная информация о конусе
«Это интересно» – 1 мин. (Слайд 17-18)
1. В геологии существует понятие «конус выноса». Это форма рельефа, образованная скоплением обломочных пород (гальки, гравия, песка), вынесенных горными реками на предгорную равнину или в более плоскую широкую долину.
2. В биологии есть понятие «конус нарастания». Это верхушка побега и корня
растений, состоящая из клеток образовательной ткани.
3. «Конусами» называют семейство морских моллюсков подкласса
Переднежаберных, попавших в Книгу рекордов Гиннеса. Раковина коническая
(2–16 см), ярко окрашенная. Конусов свыше 500 видов. Живут в тропиках и субтропиках, являются хищниками, имеют ядовитую железу. Укус конусов очень болезнен. Известны смертельные случаи. Раковины используются как украшения, сувениры. В то же время, яд некоторых моллюсков используют в фармакологии для изготовления сильнодействующих обезболивающих препаратов, не вызывающих наркотической зависимости.
4.По статистике на Земле ежегодно гибнет от разрядов молний 6 человек на
1 000 000 жителей (чаще в южных странах). Этого бы не случалось, если бы везде были громоотводы, образующие конус безопасности. Чем выше
громоотвод, тем больше объем такого конуса. Некоторые люди пытаются спрятаться от разрядов под деревом, но дерево не проводник, на нем заряды накапливаются и дерево может быть источником напряжения.
5. В физике встречается понятие «телесный угол». Это конусообразный угол,
вырезанный в шаре. Единица измерения телесного угла – 1 стерадиан. Свет от киноаппарата, прожектора распространяется в виде конуса.
VIII.Дифференцированное домашнее задание. – 1 мин.
1)Повторить §61-63, §81.
2) Всем учащимся предлагаю решить задачу по (Слайд 19) на выбор одна задача
IХ. Итог урока. Рефлексия – 2 мин.
Итак, мы с вами расширили понятие и представление о конусе, вывели формулу объем конуса. Вопрос о конусе важен, т.к. конические детали имеются во многих машинах и механизмах. Да и в жизни мы убедились, что знания о конусе отнюдь не лишние.
- Подведем итог урока. Какова была цель урока?
- Как вы считаете, достигнута ли она?
- Удовлетворены ли вы работой своей группы?
- Можете ли вы оценить работу вашей группы как способствующую достижению цели урока?
- Можете ли вы сказать, что в ходе урока произошло обогащение запаса ваших знаний?
- Какое открытие для себя вы сделали?
Закончим урок словами Яна Амоса Коменского: «Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию» (Слайд 20)
- Вы систематизировали теоретические знания о конусе, применили свои знания при решении нестандартных задач, увидели связь математики с окружающим миром.
- Мне приятно было с вами работать, и надеюсь, что знания, полученные на данном уроке геометрии, вы сможете успешно применить в различных жизненных ситуациях.
Х. Оценки за урок- 1мин.
Оценка в журнал ставится в соответствии с оценкой консультанта по итогам работы в группе и самооценкой учащегося (Слайд 21)
 литра=0,2 дм3
литра=0,2 дм3
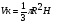
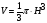 ,
, 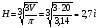
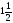 человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, вы получили бы еще более скромный результат. Таким образом, математика помогает критически относиться к художественным произведениям.
человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, вы получили бы еще более скромный результат. Таким образом, математика помогает критически относиться к художественным произведениям.








![Решите (устно) задачи: Вычислите объём конуса, если его высота 6 см, а площадь основания 42 см 2 . Объём конуса с радиусом основания 4 м и высотой 6 м равен: [84 см 3 ] [32π м 3 ]](https://fsd.kopilkaurokov.ru/up/html/2017/06/01/k_592feacbe9e08/img_user_file_592feacc6443f_6_11.jpg)