ЧТО ДРЕВНИЕ ГРЕКИ РАССКАЗЫВАЛИ О МЕДВЕДИЦАХ?
О Большой и Малой Медведицах существует много легенд. Вот одна из них. Когда-то в незапамятные времена, у царя Ликаон, правившего страной Аркадией, была дочь по имени Каллисто. Красота её была столь необыкновенной, что она рискнула соперничать с Герой - богиней и супругой всемогущего верховного бога Зевса. Ревнивая Гера в конце концов отомстила Каллисто: пользуясь своим сверхъестественным могуществом, она превратила её в безобразную медведицу. Когда сын Каллисто, юный Аркад, однажды возвратившись с охоты, увидел у дверей своего дома дикого зверя, он ничего не подозревая, чуть не убил свою мать-медведицу. Этому помешал Зевс - он удержал руку Аркада, а Каллисто навсегда взял к себе на небо, превратив в красивое созвездие - Большую Медведицу. В Малую Медведицу заодно была превращена и любимая собака Каллисто. Не остался на Земле и Аркад: Зевс и его превратил в созвездие Волопаса, обречённого навеки сторожить в небесах свою мать.
Главная звезда этого созвездия называется Арктур, что означает “страж медведицы” . Большая и Малая Медведицы являются незаходящими созвездиями, наиболее заметными на северном небе.
КАК ПЕРСЕЙ СПАС АНДРОМЕДУ
В названиях звездного неба отразился миф о герое Персее. Давным-давно, если верить древним грекам, Эфиопией правил царь по имени Цефей и царица, которую звали Кассиопея. Была у них единственная дочь красавица Андромеда. Царица очень гордилась своей дочерью и однажды имела неосторожность похвастать своей красотой и красотой своей дочери перед мифическими обитательницами моря — Нереидами. Те очень
рассердились, так как считали, что они самые красивые на свете. Нереиды пожаловались своему отцу — богу морей Посейдону, чтобы он наказал Кассиопею и Андромеду. И могущественный властелин морей послал на Эфиопию огромное морское чудовище — Кита. Из пасти Кита вырывался огонь, из ушей валил черный дым, хвост был покрыт острыми шипами. Чудовище опустошало и жгло страну, грозило гибелью всему народу. Чтобы умилостивить Посейдона, Цефей и Кассиопея согласились отдать любимую дочь на съедение чудовищу. Красавица Андромеда была прикована цепями к прибрежной скале и покорно ждала своей участи. А в это время на другом краю света один из самых известных легендарных героев — Персей — совершил необыкновенный подвиг. Он проник на остров, где жили горгоны — чудовища в образе женщин, у которых вместо волос кишели змеи. Взгляд горгон был так ужасен, что всякий, рискнувший посмотреть им в глаза, мгновенно окаменевал. Но ничто не могло остановить бесстрашного Персея. Улучив момент, когда горгоны заснули. Персей отрубил голову одной из них — самой главной, самой страшной — горгоне Медузе. В тот же момент из огромного туловища Медузы выпорхнул крылатый конь Пегас. Персей вскочил на Пегаса и помчался на родину. Пролетая над Эфиопией, он заметил прикованную к скале Андромеду, которую вот-вот должен был схватить ужасный Кит. Отважный Персей вступил в схватку с чудовищем. Долго продолжалась эта борьба. Волшебные сандалии Персея подняли его в воздух, он вонзил в спину Киту свой изогнутый меч. Кит взревел и бросился на Персея. Персей направил на чудовище мертвящий взгляд отрубленной головы Медузы, которая была прикреплена к его щиту. Чудовище окаменело и утонуло, превратившись в остров. А Персей расковал Андромеду и привез ее во дворец Цефея. Обрадованный царь отдал Андромеду в жены Персею. В Эфиопии много дней продолжался веселый пир. А на небе с тех пор горят созвездия Кассиопеи, Цефея, Андромеды, Персея. На карте звездного неба вы найдете созвездие Кита, Пегаса. Так древние мифы Земли нашли свое отражение на небе.
КАК КРЫЛАТЫЙ КОНЬ ПЕГАС “ЗАЛЕТЕЛ” НА НЕБО
Рядом с Андромедой находится созвездие Пегаса, которое особенно хорошо видно в полночь в середине октября. Три звезды этого созвездия и звезда альфа Андромеды образуют фигуру, получившую у астрономов название “Большой квадрат” . Его можно легко найти на осеннем небе. Крылатый конь Пегас возник из обезглавленного Персеем тела Медузы Горгоны, но не унаследовал от нее ничего плохого. Он был любимцем девяти муз — дочерей Зевса и богини памяти Мнемозины, на склоне горы Геликон он выбил копытом источник Иппокрены, вода которого приносила поэтам вдохновение.
И еще одна легенда, в которой упомянут Пегас. Внук царя Сисифа Беллерофонт должен был убить огнедышащее чудовище Химеру (Химера — по-гречески “коза” ) . Страшилище имело голову льва, туловище козы и хвост дракона. Беллерофонту удалось сразить Химеру с помощью Пегаса. Однажды он увидел крылатого коня, и желание завладеть им охватило юношу. Во сне к нему явилась богиня Афина, любимая дочь Зевса, мудрая и воинственная, покровительница многих героев. Она подарила
Беллерофонту чудесную, усмиряющую коней уздечку. С ее помощью Беллерофонт поймал Пегаса и отправился на битву с Химерой. Высоко поднявшись в воздух, он бросал в чудовище стрелы, пока оно не испустило дух. Но своей удачей Беллерофонт не удовлетворился, а пожелал на крылатом коне подняться на небо, в жилище бессмертных. Зевс, узнав про это, разгневался, привел Пегаса в ярость, и тот сбросил своего всадника на Землю. Пегас после этого поднялся на Олимп, где носил молнии Зевса.
Главная достопримечательность созвездия Пегаса — яркое шаровое скопление. В бинокль видно круглое светящееся туманное пятнышко, края которого искрятся, как огни большого города, видимого с борта самолета. Оказывается, в этом шаровом скоплении заключено около шести миллионов солнц!
САМОЕ КРАСИВОЕ СОЗВЕЗДИЕ ЮЖНОГО НЕБА
На всем небе нет иного созвездия, которое бы содержало столько интересных и легко доступных для наблюдения объектов, как Орион, расположенный вблизи созвездия Тельца. Орион был сыном Посейдона — бога морей по греческой мифологии (по римской — Нептун) . Он был знаменитым охотником, сражался с быком и похвалялся тем что нет животного, которого он не смог бы победить, за что Гера, могущественная супруга могущественного Зевса, наслала на него Скорпиона. Орион очистил от диких зверей остров Хиос и стал просить у царя этого острова руки его дочери, но тот отказал ему. Орион попытался похитить девушку, и царь отомстил ему: напоив допьяна, он ослепил Ориона. Гелиос возвратил Ориону зрение, но от укуса посланного Герой Скорпиона Орион все же погиб. Зевс поместил его на небе таким образом, что он может всегда уйти от своего преследователя, и действительно, эти два созвездия одновременно на небе не видны никогда.
ОТКУДА НА НЕБЕ ВОЛОСЫ ВЕРОНИКИ?
У древнего созвездия Льва на небе была довольно большая “территория” , а сам Лев был обладателем великолепной “кисточки” на хвосте. Но в 243 году до н.э. он ее лишился. Произошла забавная история, о которой гласит легенда.
У египетского царя Птолемея Эвергета была красавица супруга, царица Вероника. Особенно великолепны были ее роскошные длинные волосы. Когда Птолемей отправился на войну, его опечаленная супруга дала клятву богам: если они сохранят ее любимого мужа целым и невредимым, принести в жертву свои волосы. Вскоре Птолемей благополучно вернулся домой, но, увидев остриженную супругу, был расстроен. Царственную чету несколько успокоил астроном Конон, заявив, что боги вознесли волосы Вероники на небо, где им предназначено украшать весенние ночи.
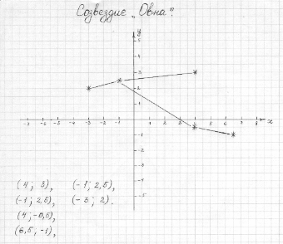
СОЗВЕЗДИЕ ОВНА
Созвездие Овна также было весьма почитаемо в древности. Верховный бог Египта Амон-Ра изображался с бараньей головой, а дорога к его храму представляла собой аллею из сфинксов с бараньими головами. Считалось, что созвездие Овна названо в честь Овна с золотым руном, за которым и плыли аргонавты. На небе, кстати, существует ряд созвездий, отражающих корабль Арго. Звезда альфа (самая яркая) этого созвездия называется Гамаль (по-арабски “взрослый баран” ) . Самая яркая звезда в созвездии Тельца носит название Альдебаран.
КАК НА НЕБЕ ПОЯВИЛСЯ РАК
Созвездие Рака - одно из самых малозаметных зодиакальных созвездий. История его очень интересна. Существует несколько довольно экзотических объяснений происхождения названия этого созвездия. Так, например, всерьез утверждалось, что египтяне поместили в эту область неба Рака как символ разрушения и смерти, потому что это животное питается падалью. Рак движется хвостом вперед. Около двух тысяч лет назад в созвездии Рака находилась точка летнего солнцестояния (т.е. самая большая продолжительность светового дня) . Солнце, достигнув в это время предельного удаления к северу начинало “пятиться” назад. Продолжительность дня постепенно уменьшалось.
По классической древней мифологии огромный морской Рак напал на Геракла, когда он боролся с Лернейской Гидрой. Герой раздавил его, но богиня Гера, ненавидевшая Геракла, поместила Рака на небо.
В Лувре хранится знаменитый египетский круг зодиака, в котором созвездие Рака располагается выше всех остальных.
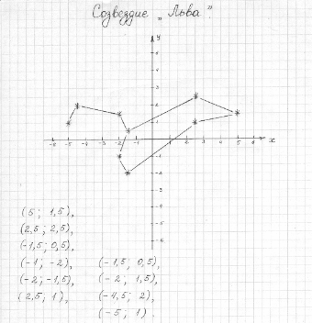
СТРАШЕН ЛИ ЛЕВ НА НЕБЕ?
Около 4,5 тысяч лет назад в этом созвездии находилась точка летнего солнцестояния, и Солнце оказывалось в этом созвездии в самое жаркое время года. Поэтому у многих народов именно Лев стал символом огня.
Ассирийцы так и называли это созвездие “великий огонь” , и халдеи связывали свирепого льва с не менее свирепой жарой, Которая была каждое лето. Они полагали, что Солнце получает дополнительную силу и теплоту, находясь среди звёзд льва.
В Египте тоже связывали это созвездие с летним периодом: стаи львов, спасаясь от жары, перекочевали из пустыни в долину Нила, который в это время разливался. Поэтому египтяне помещали на затворах шлюзов
ирригационных каналов, направлявших воду на поля, изображения в виде львиной головы с открытой пастью.
ВЕСЫ — ЕДИНСТВЕННОЕ “НЕЖИВОЕ”
ЗОДИАКАЛЬНОЕ СОЗВЕЗДИЕ
Действительно, кажется странным, что среди животных и “полуживотных” в Зодиаке есть знак Весы.
Свыше двух тысячелетий назад в этом созвездии находилась точка осеннего равноденствия. Равенство дня и ночи могло стать одной из причин, по которой зодиакальное созвездие получило название “Весы” .
Появление на небе Весов в средних широтах указывало, что пришло время сева, а древние египтяне уже в конце весны могли рассматривать это как сигнал к началу уборки первого урожая. Весы — символ равновесия — могли просто напоминать древним земледельцам о необходимости взвесить собранный урожай.
У древних греков Астрея — богиня справедливости с помощью Весов взвешивала судьбы людей. Один из мифов объясняет появление зодиакального созвездия Весы как напоминание людям о необходимости строго соблюдать законы. Дело в том, что Астрея была дочерью всемогущего Зевса и богини правосудия Фемиды. По поручению Зевса и Фемиды Астрея регулярно “инспектировала” Землю (вооружившись весами и завязав повязкой глаза, дабы судить обо всем объективно, снабжать Олимп добротной информацией и беспощадно карать обманщиков, лжецов и всех, кто осмеливался свершить всякого рода несправедливые поступки) . Вот Зевс и решил, что Весы дочери следует поместить на небо.


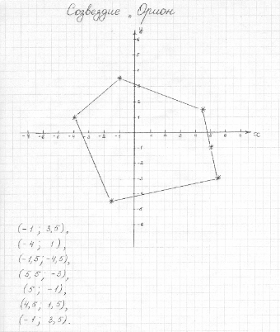
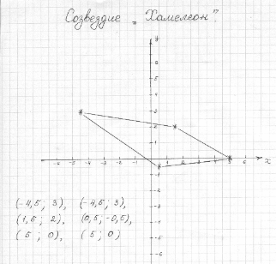
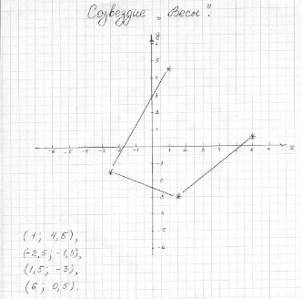


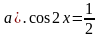
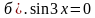
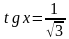
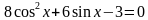
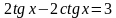
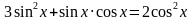
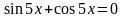
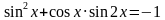 .
.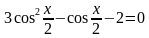
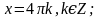
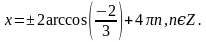
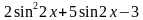 =0
=0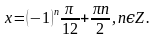
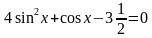
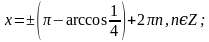
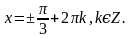
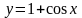 и
и 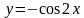 ?
?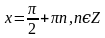 ;
; 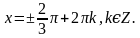
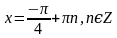 ,
, 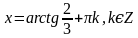 .
.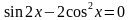
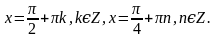
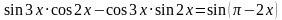
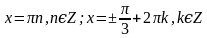
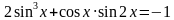 . Найти все корни, принадлежащие [0; 2π]
. Найти все корни, принадлежащие [0; 2π]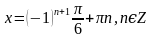 (общее решение),
(общее решение), 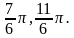
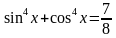
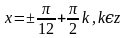 .
.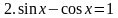
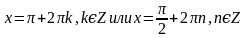 .
.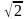 .
.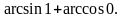
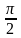
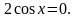
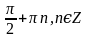
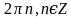
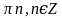 Г.
Г. 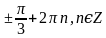
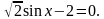
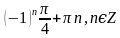 Б.
Б. 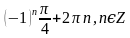 В.
В. 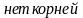 Г.
Г. 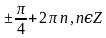
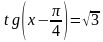 .
.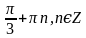 Б.
Б. 





















