в данной работе представлен конспект и технологическая карта урока геометрии в 8 классе с применением мультимедийных презентаций. Урок проведён в ходе аттестации на высшую квалификационную категорию, высоко оценен членами областной аттестационной комиссии, без замечаний по методике проведения.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Урок в 8-ом классе теорема Пифагора
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Заявка участника»
Просмотр содержимого документа
«Конспект урока по геометрии в 8»
Просмотр содержимого документа
«Технологическая карта урока по геометрии в 8»
Просмотр содержимого документа
«приложение 1 - расшифруем тему урока»
Просмотр содержимого документа
«приложение 2 - доклад по истории Теоремы Пифагора»
Просмотр содержимого документа
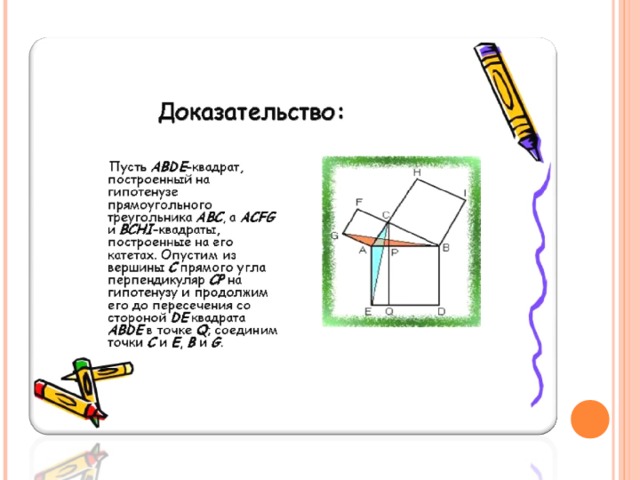
«приложение 3 доказательство теоремы»
Просмотр содержимого документа
«приложение 4»
Просмотр содержимого документа
«приложение 5»
Просмотр содержимого документа
«приложение 6»
Просмотр содержимого презентации
«приложение 23 история Пифагора»
Полезное для учителя
Распродажа видеоуроков!
1790 руб.
2560 руб.
1630 руб.
2330 руб.
2000 руб.
2860 руб.
1670 руб.
2380 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства




 Перед вами лежат карточки (Приложение 1), на них изображены фигуры. Найдите площадь каждой фигуры. Буквы, соответствующие верным ответам, вы видите на экране. (Слайд №2).
Перед вами лежат карточки (Приложение 1), на них изображены фигуры. Найдите площадь каждой фигуры. Буквы, соответствующие верным ответам, вы видите на экране. (Слайд №2).  Итак, все площади найдены, таблица заполнена. У меня к вам вопрос: Какова же тема урока? (Теорема Пифагора). (Слайд №3).
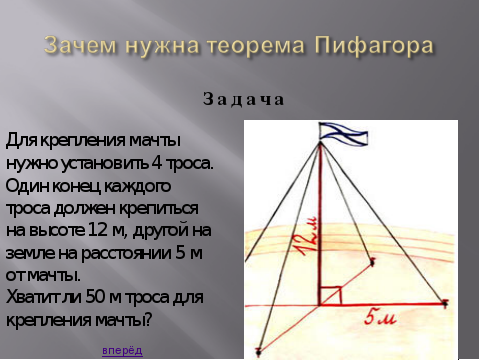
Итак, все площади найдены, таблица заполнена. У меня к вам вопрос: Какова же тема урока? (Теорема Пифагора). (Слайд №3).  Сначала выясним, а нужна ли вообще эта теорема. Потом, как и всякую теорему, её надо доказать. Конечно же, необходимо рассмотреть примеры применения при решении задач. Ну и наконец, научиться самим применять эту теорему.
Сначала выясним, а нужна ли вообще эта теорема. Потом, как и всякую теорему, её надо доказать. Конечно же, необходимо рассмотреть примеры применения при решении задач. Ну и наконец, научиться самим применять эту теорему.


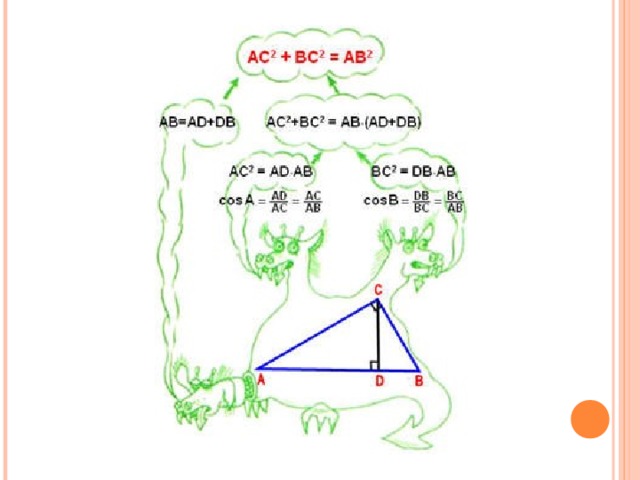
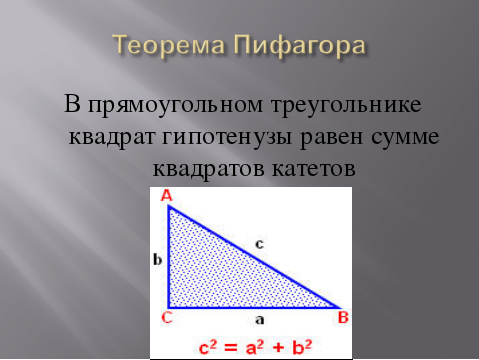 Давайте запишем в тетрадь современную её формулировку и сделаем соответствующий рисунок. (Слайд №9).
Давайте запишем в тетрадь современную её формулировку и сделаем соответствующий рисунок. (Слайд №9). 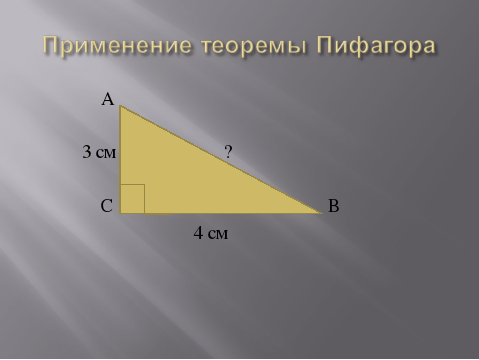 Дальше мы должны научиться применять эту теорему при решении задач. Рассмотрим задачу №1. (Слайд №10).
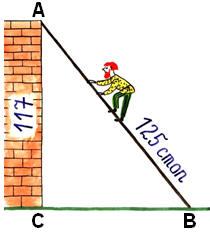
Дальше мы должны научиться применять эту теорему при решении задач. Рассмотрим задачу №1. (Слайд №10). 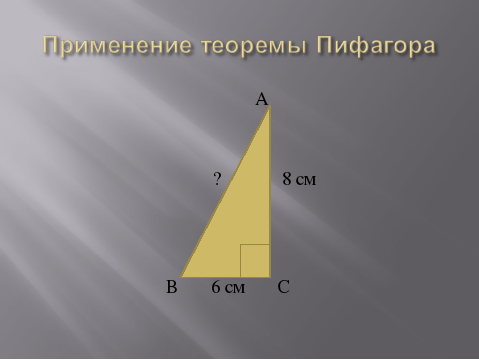 Один из учащихся рассказывает о решении задачи устно. Дан прямоугольный треугольник. В нём известны катеты АС = 8 см, ВС = 6 см. Найти гипотенузу АВ. Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора с2 = а2 + b2, с2 = 62 + 82, с2 = 36 + 64, с2 = 100, с = 10 см. Ответ: 10 см.
Один из учащихся рассказывает о решении задачи устно. Дан прямоугольный треугольник. В нём известны катеты АС = 8 см, ВС = 6 см. Найти гипотенузу АВ. Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора с2 = а2 + b2, с2 = 62 + 82, с2 = 36 + 64, с2 = 100, с = 10 см. Ответ: 10 см.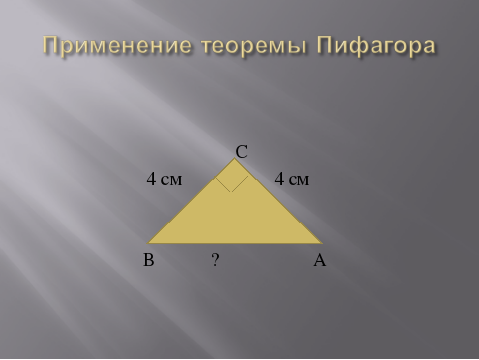 у а задачу №3, которую вы видите на экране, полностью оформите в тетради с рисунком и решением. (Слайд № 12).
у а задачу №3, которую вы видите на экране, полностью оформите в тетради с рисунком и решением. (Слайд № 12).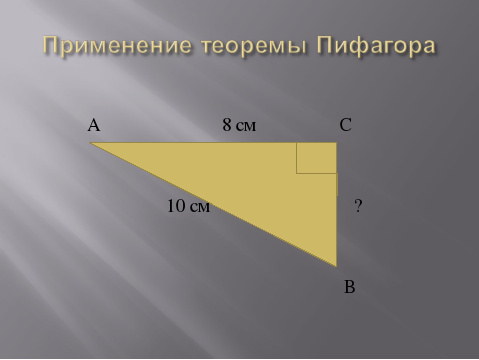





 По одной из легенд отцом Пифагора был сириец Мнесарх. Однажды по торговым делам он прибыл из своего родного Тира на остров Самос. Год был неурожайным, население голодало, и Мнесарх устроил бесплатную раздачу хлеба народу. В благодарность его удостоили самосского гражданства.
По одной из легенд отцом Пифагора был сириец Мнесарх. Однажды по торговым делам он прибыл из своего родного Тира на остров Самос. Год был неурожайным, население голодало, и Мнесарх устроил бесплатную раздачу хлеба народу. В благодарность его удостоили самосского гражданства. 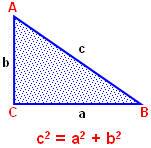
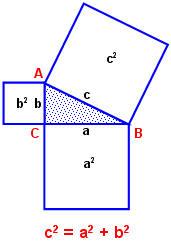




 – гипотенуза b а
– гипотенуза b а
 2 = а2 + b2 а с с b
2 = а2 + b2 а с с b
 b с с
b с с
 А №1. Решение:
А №1. Решение: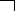 треугольник АВС.
треугольник АВС. 
 ешение:
ешение: