Урок обобщения и систематизации знаний по теме «Четырёхугольники».

Дополнительные задачи:

1. Периметр прямоугольника равен 48 см. Найдите его стороны, если относятся как 1:2.

2) Дано: АВСД – ромб

∟ВАС = 40⁰

Найти: ∟В, ∟Д, ∟ДСВ, ∟ВАД

3) Дано:

А

ВД = 18 см

АС = 10 см

ВС =6 см

Д

С

Найти: Р_∆ВОС

4) Дано:

АВСД – ромб

∟ДАВ = 100⁰

Найти ∟_∆АОД

5) Сторона ромба равна 5 см. Чему равен периметр ромба?

6) Дано:

АВСД – ромб

∟ВАО = ∟АВО +20⁰

Найти ∟А, ∟В, ∟С, ∟Д

7) Периметр прямоугольника равен 128 см. Большая сторона его равна 44 см. Чему равна меньшая сторона прямоугольника?

8) Сумма двух острых углов ромба равна 160⁰. Чему равен тупой угол ромба?

9) Основания трапеции равны 8 и 14 см. Найдите среднюю линию трапецию.

10) Дано:

АВСД - прямоугольник

АС = 10 см

СД =4 см

Найти: Р _∆ сод

11) Одна из сторон параллелограмма в 4 раза больше другой, а его периметр равен 30 см. Чему равны стороны параллелограмма?

Конспект урока по геометрии в 9 классе.

Учитель математики Булдыгина Ольга Адольфовна, МОУ Помоздинская СОШ, Республика Коми.

Тема: Урок обобщения и систематизации знаний по теме «Четырёхугольники».

Цель: 1.Систематизировать основные определения, свойства, признаки по темам: «Параллелограмм. Прямоугольник. Ромб. Квадрат. Трапеция».

2.Установить связь между основными фигурами, изучаемыми по данной теме.

3.Активизировать работу учащихся, вызвать интерес к предмету.

Ход урока:

1)Организационный момент.

2)Сообщение темы и цели урока.

- Сегодня на уроке мы с вами должны повторить тему «Четырёхуголь- ники», систематизировать полученные знания и в конце урока ответить на вопрос: «Почему генеалогическое дерево четырёхугольников выросло именно таким образом?» (Слайд № 2) Сегодня каждый получит оценку, а вот какую, зависит от вас, поэтому жду активной работы на уроке.

3)Проверка д/з. (№ 65 и 69 по учебнику А.В.Погорелова)

4)Фронтальный опрос:

- Что называется трапецией?

- Какая трапеция называется равнобокой?

- Что такое средняя линия трапеции?

-Доказать теорему 6.8.

5)Повторение и обобщение.

-За урок мы с вами заполним таблицу «Сравнение четырёхугольников» (Приложение 1)

- Для начала вспомним первый урок геометрии в 8 классе.

- Какие из трёх фигур являются четырёхугольниками? Почему? (Слайд 3)

- Какая фигура называется четырёхугольником? (Определение)

(Слайд 4, таблица пустая, учитель объясняет, как нужно её заполнять)

По ходу заполнения таблицы решаются устные задачи на данные фигуры.

6)Самостоятельная работа по карточкам на 5 минут (Заранее спланировать учителю кому какую дать) и разбор этих задач.

(Приложение 2)

7)Итог урока.

- Так почему же генеалогическое дерево четырёхугольников выросло именно таким образом? Вернуться к дереву.( Слайд параллелограммы и не параллелограммы).

8)Рефлексия. (Что было самым сложным на сегодняшнем уроке?)

9)Д/з: Составьте родословную совместно с родителями.

Булдыгина Ольга Адольфовна

Учитель математики

МОУ Помоздинская СОШ им.В.Т.Чисталева

Урок обобщения и систематизации знаний по теме «Четырехугольники»

Генеалогическое дерево четырехугольников

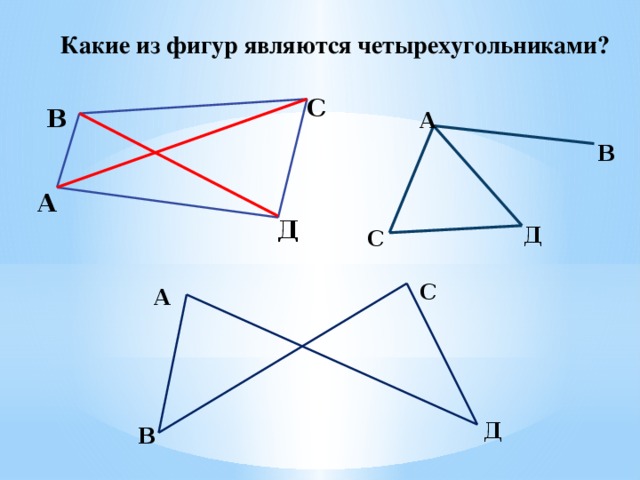
Какие из фигур являются четырехугольниками?

С

В

А

В

А

Д

Д

С

С

А

Д

В

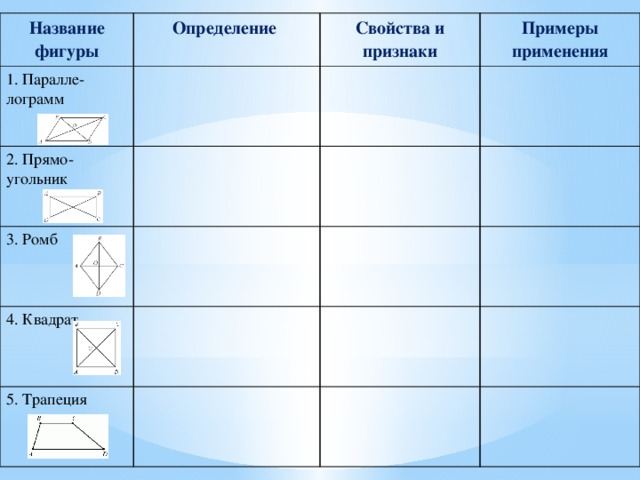
Название фигуры

Определение

1. Паралле-лограмм

2. Прямо-угольник

Свойства и признаки

Примеры применения

3. Ромб

4. Квадрат

5. Трапеция

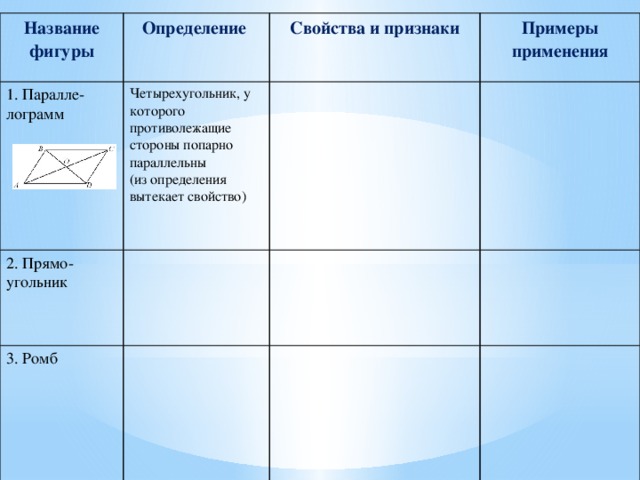
Название фигуры

Определение

1. Паралле-лограмм

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

(из определения вытекает свойство)

Примеры применения

3. Ромб

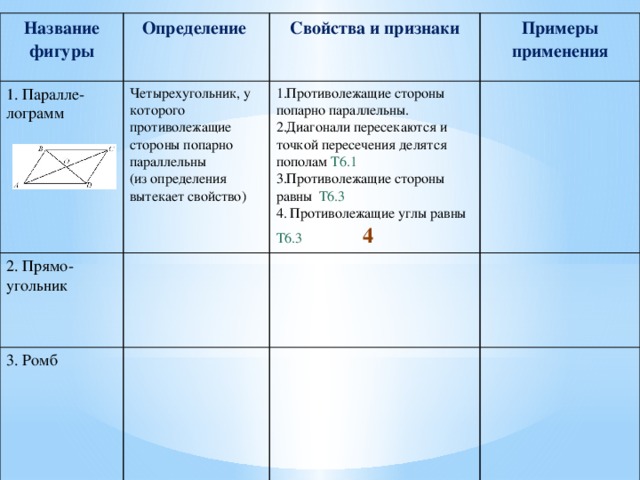
Название фигуры

Определение

1. Паралле-лограмм

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

(из определения вытекает свойство)

Примеры применения

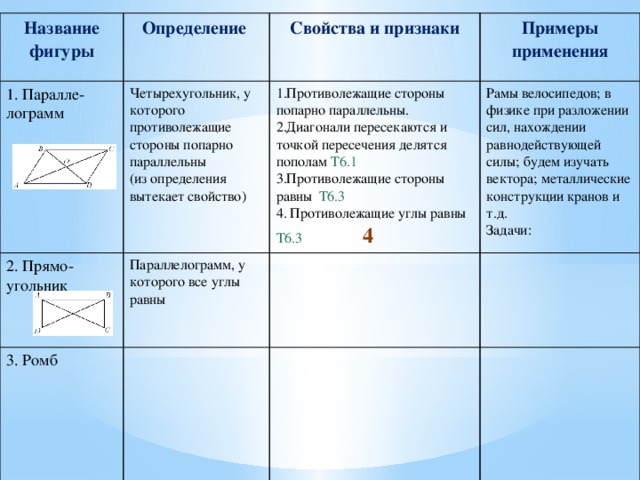
• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

4. Противолежащие углы равны Т6.3 4

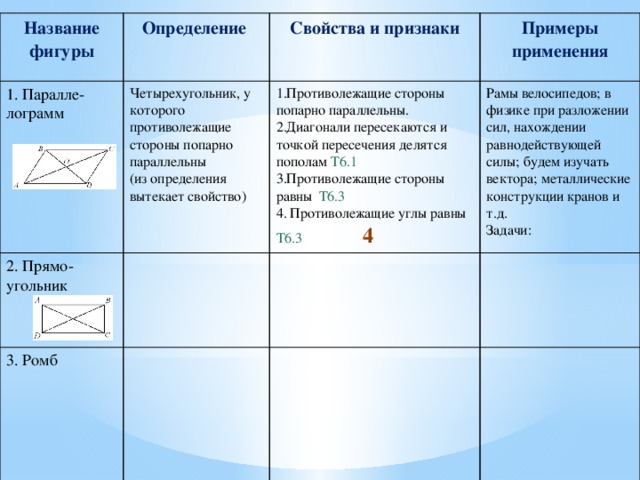
Название фигуры

Определение

1. Паралле-лограмм

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

(из определения вытекает свойство)

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

4. Противолежащие углы равны Т6.3 4

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

Задачи:

Название фигуры

1. Паралле-лограмм

Определение

2. Прямо-угольник

Четырехугольник, у которого противолежащие стороны попарно параллельны

Свойства и признаки

(из определения вытекает свойство)

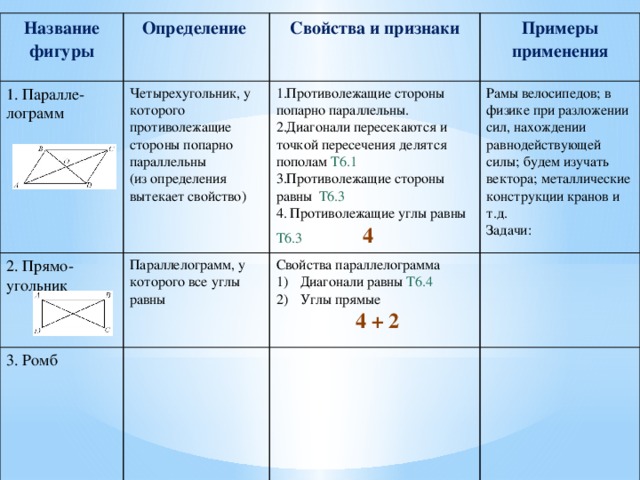
Параллелограмм, у которого все углы равны

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

4. Противолежащие углы равны Т6.3 4

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

Задачи:

Название фигуры

1. Паралле-лограмм

Определение

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

(из определения вытекает свойство)

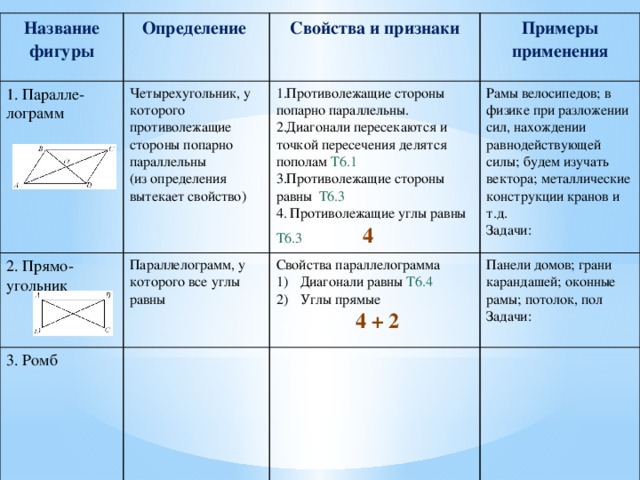
Параллелограмм, у которого все углы равны

3. Ромб

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

4. Противолежащие углы равны Т6.3 4

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

Свойства параллелограмма

Задачи:

• Диагонали равны Т6.4
• Углы прямые

4 + 2

Название фигуры

1. Паралле-лограмм

Определение

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

Параллелограмм, у которого все углы равны

(из определения вытекает свойство)

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

4. Противолежащие углы равны Т6.3 4

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

Свойства параллелограмма

Панели домов; грани карандашей; оконные рамы; потолок, пол

• Диагонали равны Т6.4
• Углы прямые

Задачи:

Задачи:

4 + 2

Название фигуры

1. Паралле-лограмм

Определение

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

Параллелограмм, у которого все углы равны

(из определения вытекает свойство)

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

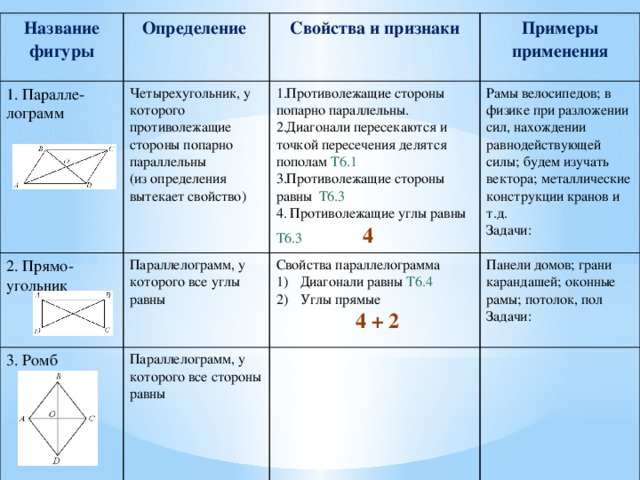
Параллелограмм, у которого все стороны равны

Свойства параллелограмма

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

4. Противолежащие углы равны Т6.3 4

Задачи:

• Диагонали равны Т6.4
• Углы прямые

Панели домов; грани карандашей; оконные рамы; потолок, пол

Задачи:

4 + 2

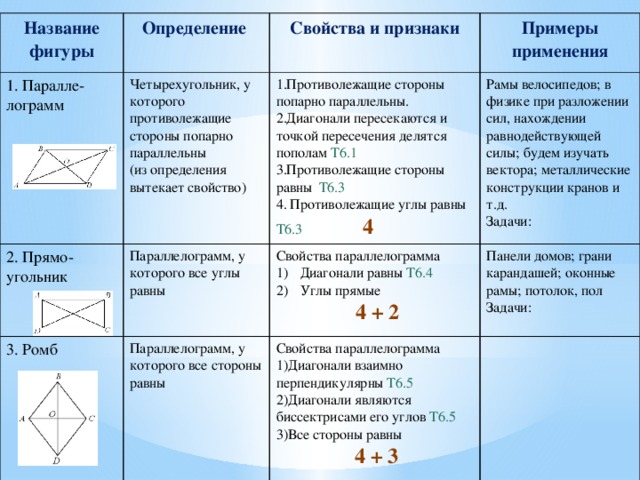
Название фигуры

1. Паралле-лограмм

Определение

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

Параллелограмм, у которого все углы равны

(из определения вытекает свойство)

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

Параллелограмм, у которого все стороны равны

Свойства параллелограмма

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

4. Противолежащие углы равны Т6.3 4

• Диагонали равны Т6.4
• Углы прямые

Задачи:

Панели домов; грани карандашей; оконные рамы; потолок, пол

Свойства параллелограмма

Задачи:

• Диагонали взаимно перпендикулярны Т6.5
• Диагонали являются биссектрисами его углов Т6.5
• Все стороны равны

4 + 2

4 + 3

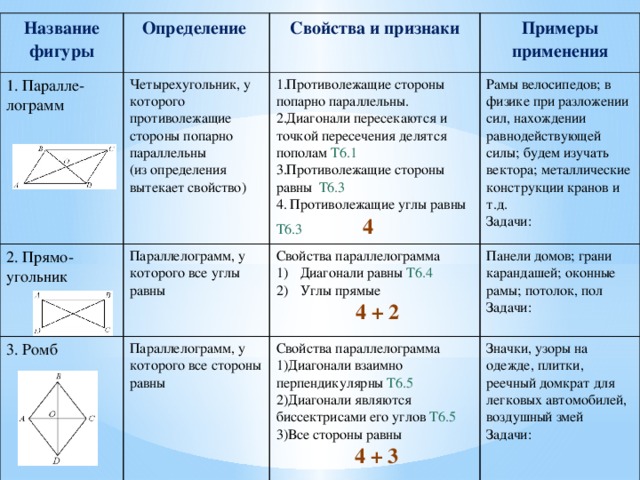
Название фигуры

Определение

1. Паралле-лограмм

Четырехугольник, у которого противолежащие стороны попарно параллельны

2. Прямо-угольник

Свойства и признаки

(из определения вытекает свойство)

Параллелограмм, у которого все углы равны

Примеры применения

• Противолежащие стороны попарно параллельны.
• Диагонали пересекаются и точкой пересечения делятся пополам Т6.1
• Противолежащие стороны равны Т6.3

3. Ромб

4. Противолежащие углы равны Т6.3 4

Рамы велосипедов; в физике при разложении сил, нахождении равнодействующей силы; будем изучать вектора; металлические конструкции кранов и т.д.

Свойства параллелограмма

Параллелограмм, у которого все стороны равны

Панели домов; грани карандашей; оконные рамы; потолок, пол

• Диагонали равны Т6.4
• Углы прямые

Задачи:

Свойства параллелограмма

Задачи:

4 + 2

• Диагонали взаимно перпендикулярны Т6.5
• Диагонали являются биссектрисами его углов Т6.5
• Все стороны равны

Значки, узоры на одежде, плитки, реечный домкрат для легковых автомобилей, воздушный змей

Задачи:

4 + 3

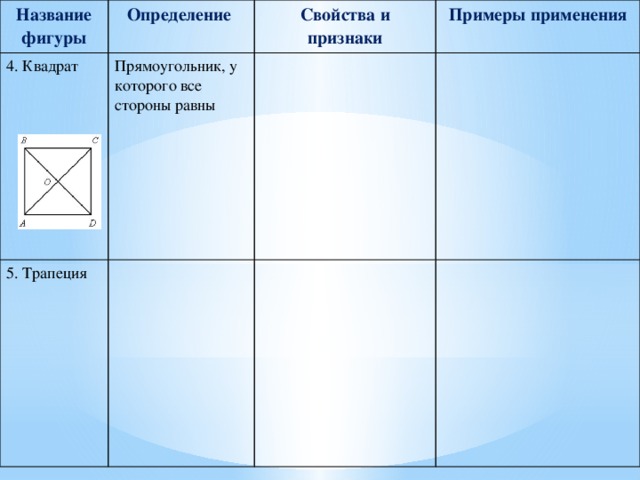
Название фигуры

Определение

4. Квадрат

Свойства и признаки

Прямоугольник, у которого все стороны равны

5. Трапеция

Примеры применения

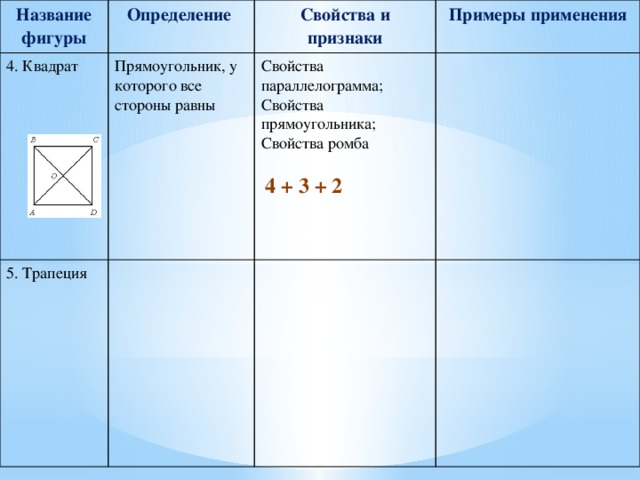
Название фигуры

Определение

4. Квадрат

Свойства и признаки

Прямоугольник, у которого все стороны равны

5. Трапеция

Примеры применения

Свойства параллелограмма;

Свойства прямоугольника;

Свойства ромба

4 + 3 + 2

Название фигуры

Определение

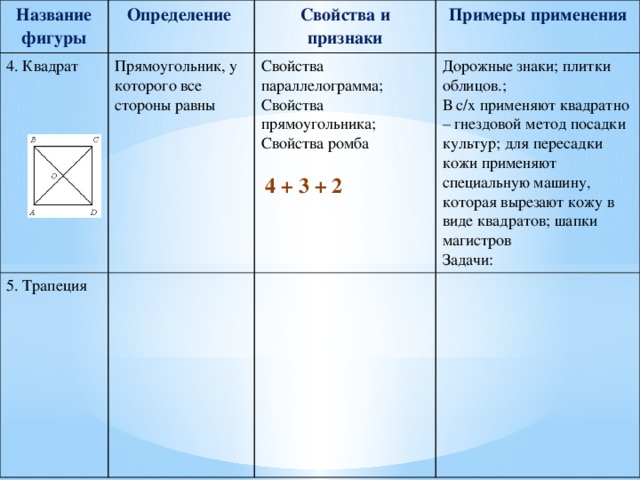
4. Квадрат

Свойства и признаки

Прямоугольник, у которого все стороны равны

5. Трапеция

Примеры применения

Свойства параллелограмма;

Свойства прямоугольника;

Дорожные знаки; плитки облицов.;

В с/х применяют квадратно – гнездовой метод посадки культур; для пересадки кожи применяют специальную машину, которая вырезают кожу в виде квадратов; шапки магистров

Свойства ромба

Задачи:

4 + 3 + 2

Название фигуры

Определение

4. Квадрат

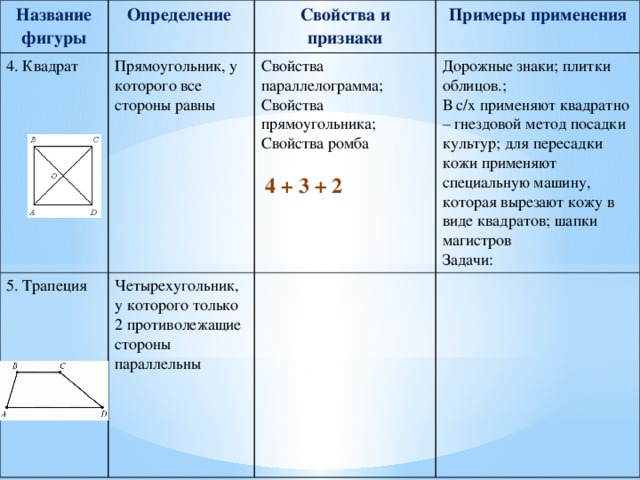
5. Трапеция

Свойства и признаки

Прямоугольник, у которого все стороны равны

Примеры применения

Свойства параллелограмма;

Четырехугольник, у которого только 2 противолежащие стороны параллельны

Свойства прямоугольника;

Дорожные знаки; плитки облицов.;

Свойства ромба

В с/х применяют квадратно – гнездовой метод посадки культур; для пересадки кожи применяют специальную машину, которая вырезают кожу в виде квадратов; шапки магистров

Задачи:

4 + 3 + 2

Название фигуры

Определение

4. Квадрат

Свойства и признаки

Прямоугольник, у которого все стороны равны

5. Трапеция

Примеры применения

Свойства параллелограмма;

Четырехугольник, у которого только 2 противолежащие стороны параллельны

Дорожные знаки; плитки облицов.;

Свойства прямоугольника;

• В равнобокой трапеции диагонали и углы при основаниях соответственно равны.
• В прямоугольной трапеции одна из боковых сторон перпендикулярна основанию

В с/х применяют квадратно – гнездовой метод посадки культур; для пересадки кожи применяют специальную машину, которая вырезают кожу в виде квадратов; шапки магистров

Свойства ромба

Задачи:

4 + 3 + 2

Название фигуры

Определение

4. Квадрат

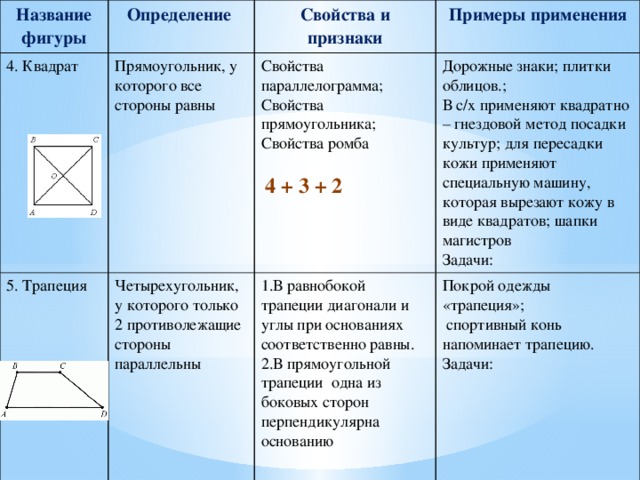
5. Трапеция

Свойства и признаки

Прямоугольник, у которого все стороны равны

Примеры применения

Свойства параллелограмма;

Четырехугольник, у которого только 2 противолежащие стороны параллельны

Свойства прямоугольника;

• В равнобокой трапеции диагонали и углы при основаниях соответственно равны.
• В прямоугольной трапеции одна из боковых сторон перпендикулярна основанию

Дорожные знаки; плитки облицов.;

Покрой одежды «трапеция»;

В с/х применяют квадратно – гнездовой метод посадки культур; для пересадки кожи применяют специальную машину, которая вырезают кожу в виде квадратов; шапки магистров

Свойства ромба

Задачи:

спортивный конь напоминает трапецию.

4 + 3 + 2

Задачи:

С

В

14

?

О

18

14

Д

А

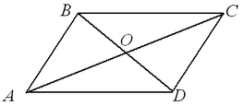
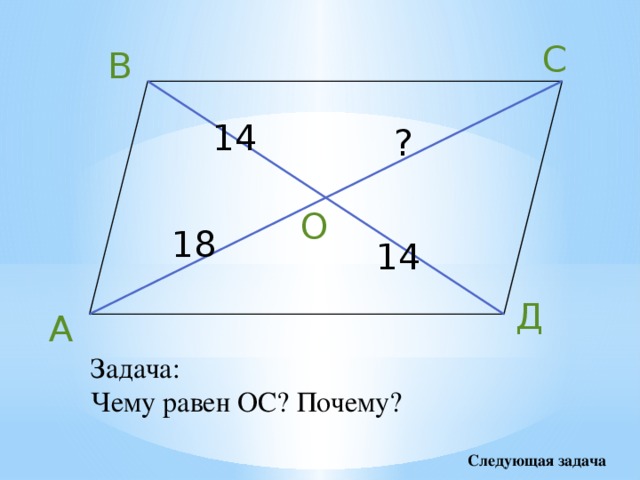
Задача:

Чему равен ОС? Почему?

Следующая задача

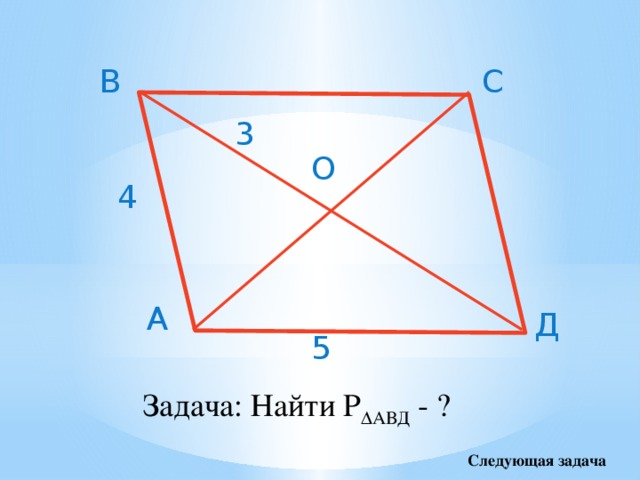
В

С

3

О

4

А

Д

5

Задача: Найти Р ∆АВД - ?

Следующая задача

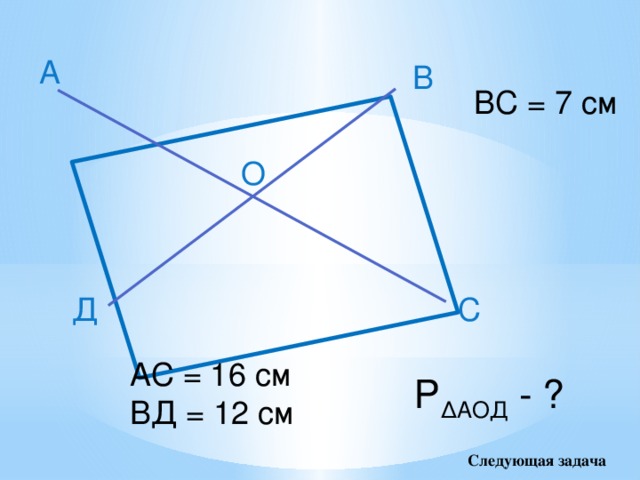
А

В

ВС = 7 см

О

Д

С

АС = 16 см

ВД = 12 см

Р ∆АОД - ?

Следующая задача

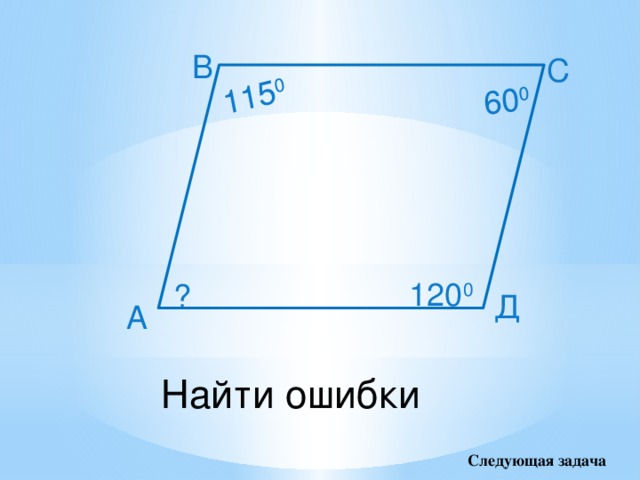
60 0

115 0

В

С

120 0

?

Д

А

Найти ошибки

Следующая задача

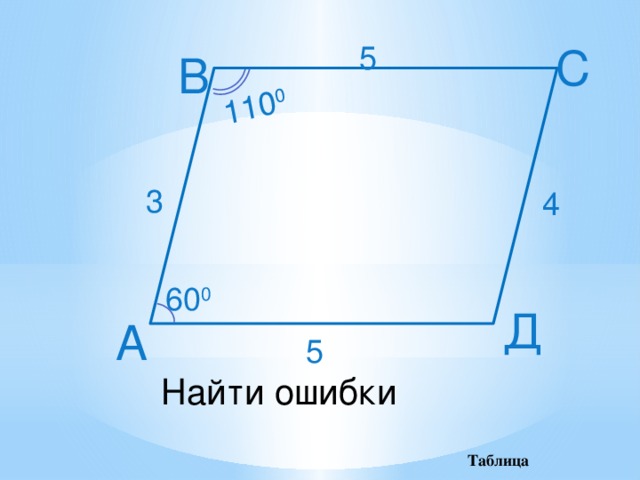
110 0

С

5

В

3

4

60 0

Д

А

5

Найти ошибки

Таблица

А

в

35 0

?

Д

с

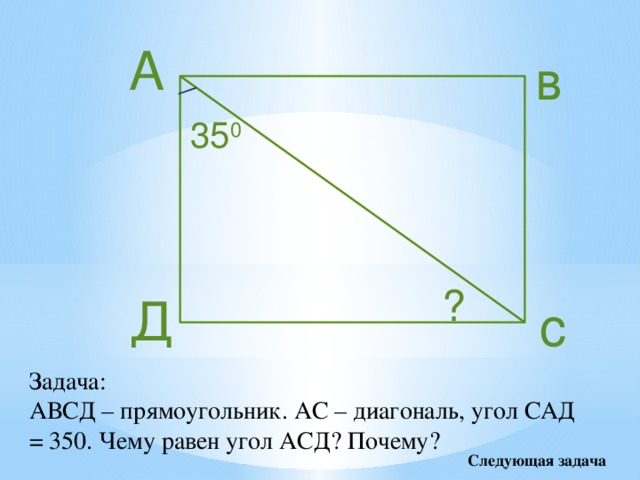
Задача:

АВСД – прямоугольник. АС – диагональ, угол САД = 350. Чему равен угол АСД? Почему?

Следующая задача

А

В

0

С

Д

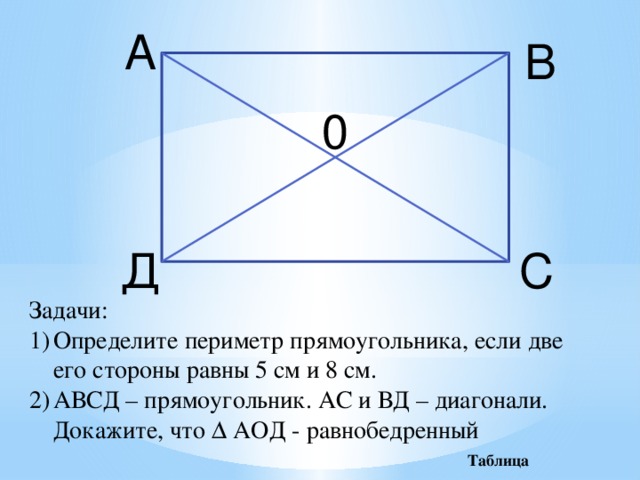
Задачи:

• Определите периметр прямоугольника, если две его стороны равны 5 см и 8 см.
• АВСД – прямоугольник. АС и ВД – диагонали. Докажите, что ∆ АОД - равнобедренный

Таблица

В

А

С

О

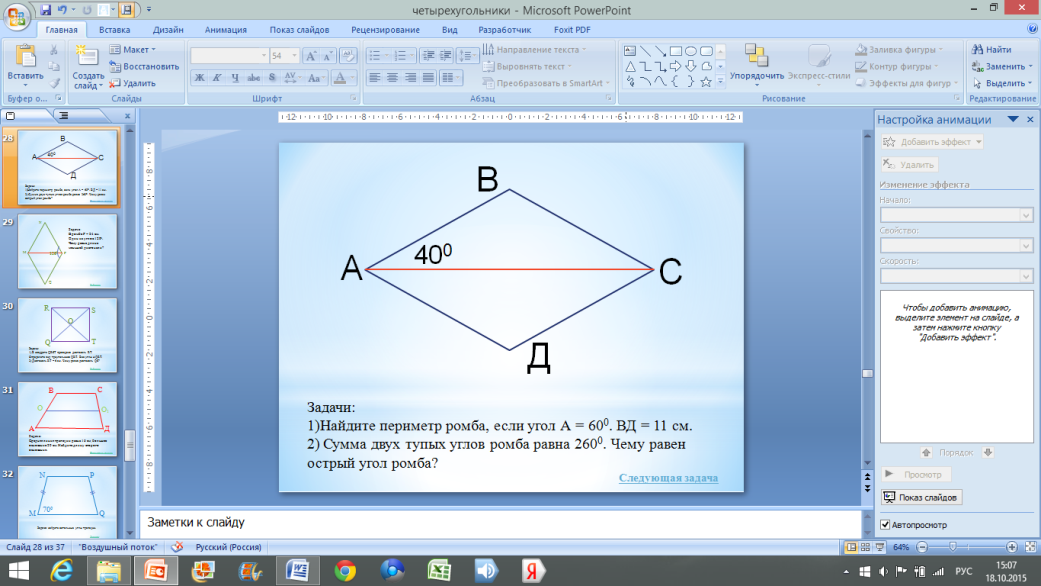
Д

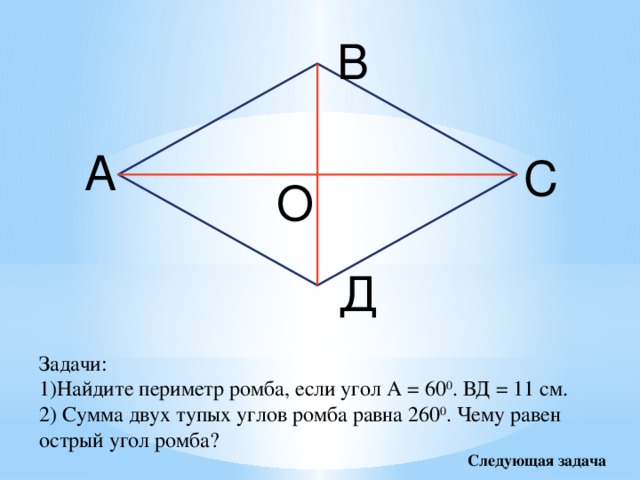
Задачи:

1)Найдите периметр ромба, если угол А = 60 0 . ВД = 11 см.

2) Сумма двух тупых углов ромба равна 260 0 . Чему равен острый угол ромба?

Следующая задача

N

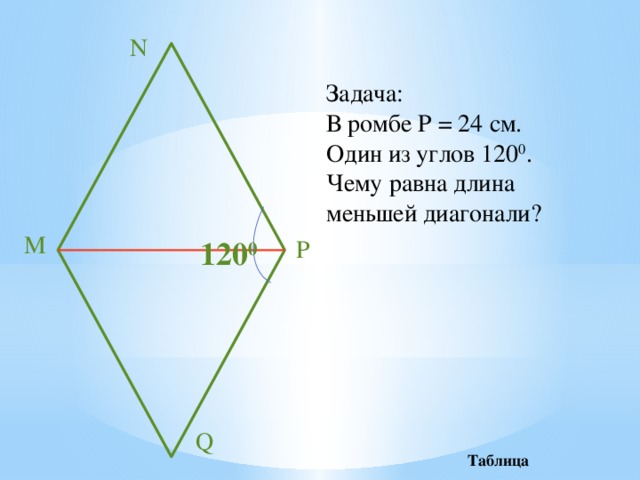
Задача:

В ромбе Р = 24 см.

Один из углов 120 0 .

Чему равна длина меньшей диагонали?

M

P

120 0

Q

Таблица

R

S

O

T

Q

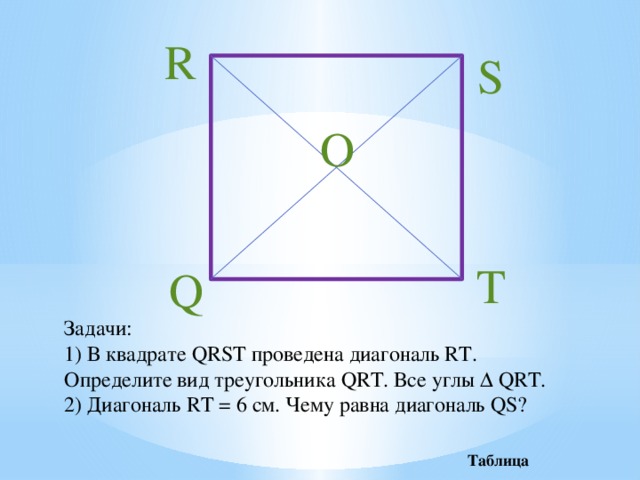
Задачи:

1) В квадрате QRST проведена диагональ RT. Определите вид треугольника QRT. Все углы ∆ QRT.

2) Диагональ RT = 6 см. Чему равна диагональ QS?

Таблица

С

В

О

О 1

А

Д

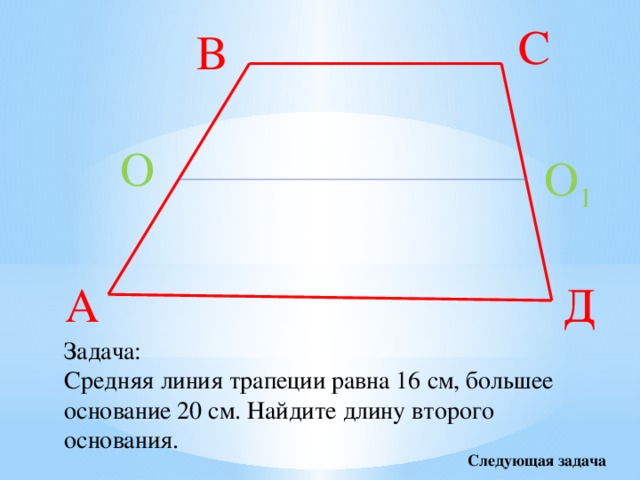
Задача:

Средняя линия трапеции равна 16 см, большее основание 20 см. Найдите длину второго основания.

Следующая задача

P

N

70 0

M

Q

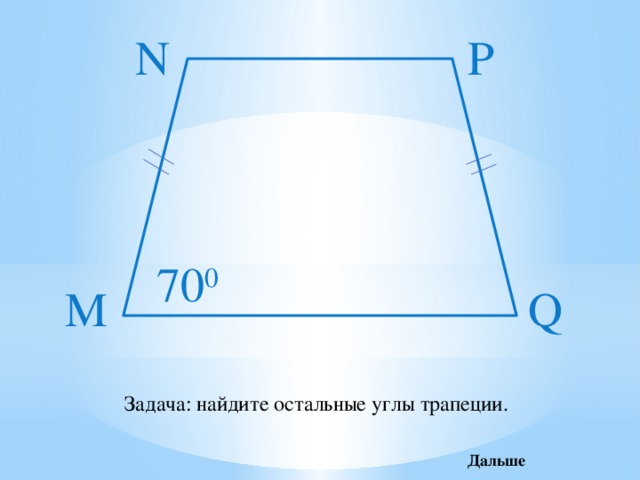
Задача: найдите остальные углы трапеции.

Дальше

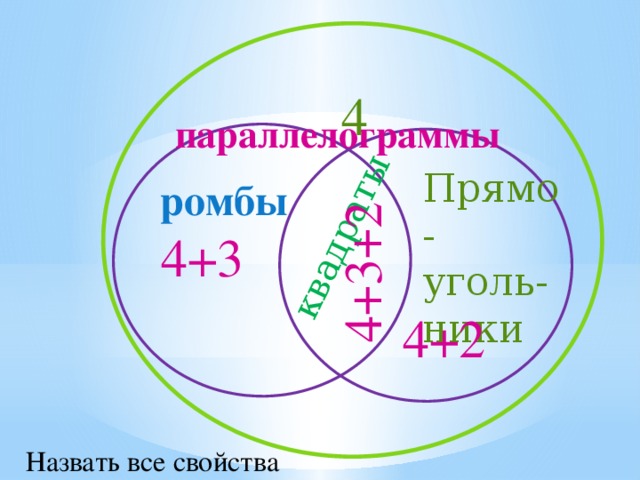
квадраты

4+3+2

параллелограммы

4

Прямо-уголь-ники

ромбы

4+3

4+2

Назвать все свойства

• Параллелограммы

• Не параллелограммы

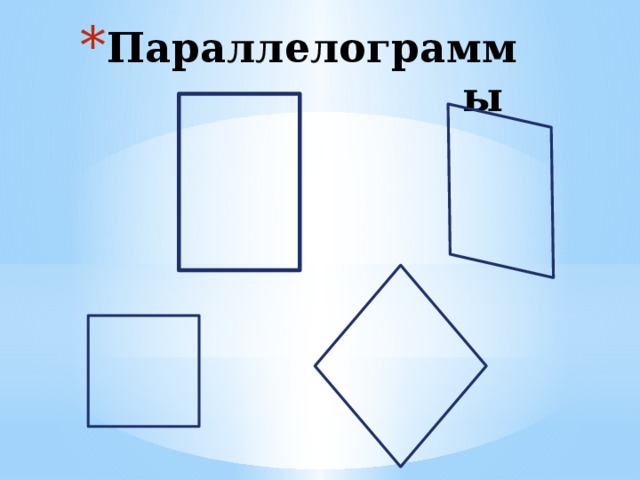
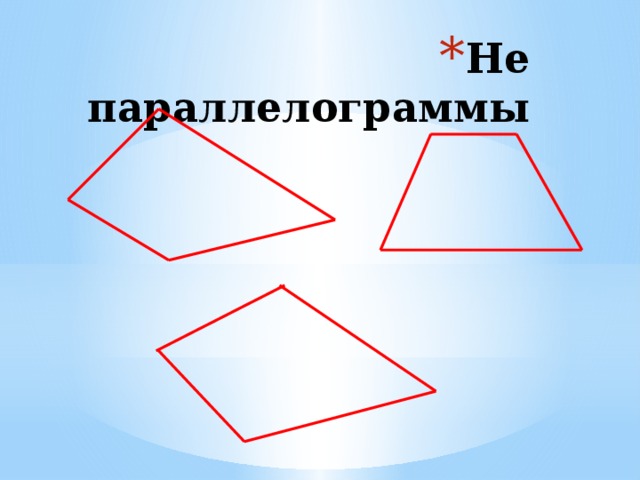
Решить дополнительные задачи

• Д/з: Составьте родословную совместно с родителями.

• Спасибо за внимание!