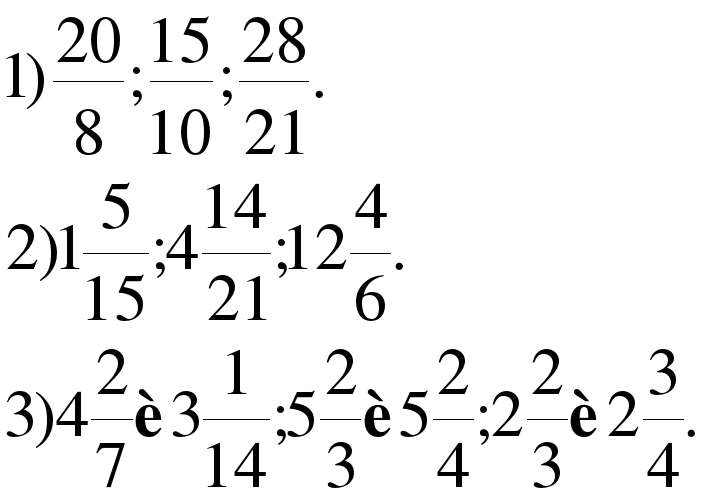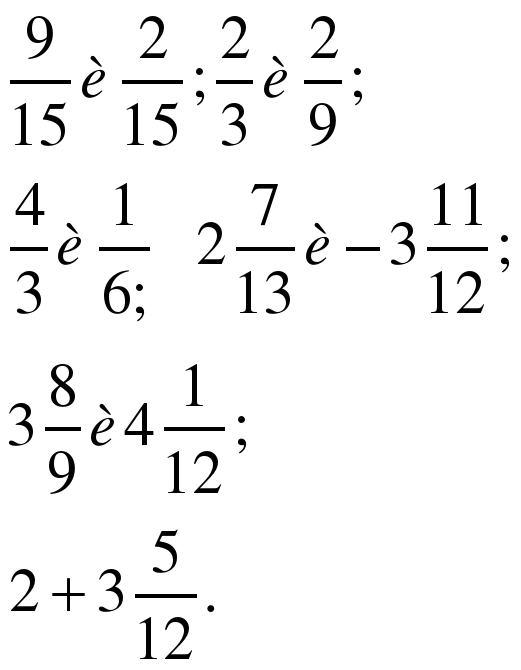1.
| Этапы урока | Учитель | Ученики | Доска и оборудование |
| Организационный этап | Учитель просит учеников вместе вспомнить правила поведения на уроке .Слайд 2. Предлагает девиз урока . Произносит девиз урока «Лучший способ изучить что-либо – это открыть самому». Слайд 3. Сегодня у нас урок изучения нового, по какому плану мы будем работать?
Какие умения (общеучебные) будем развивать? |
Ученики хором произносят девиз. Ученики вступают в диалог с учителем: 1.Вспоминаем то, что важно для урока. 2. Определяем основной вопрос урока. 3. Открываем новые знания. 4. Применяем новые знания. Ученики вступают в диалог с учителем: -умение планировать свою работу; -умение ставить цель; -умение оценивать себя; -умение договариваться. Слайд 5. |
На доске высвечиваются пункты плана. Слайд 4. |
| Актуализация знаний (вспоминаем то, что важно для урока) | Обратите внимание на числа записанные на доске. 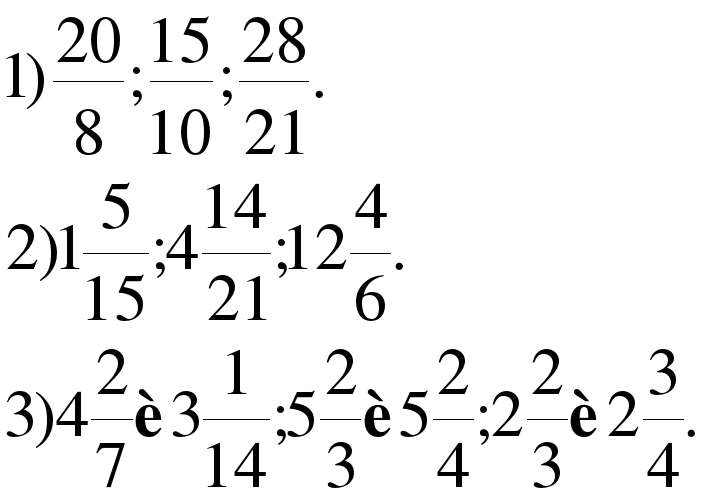
Что это за числа? Как они называются? Какие задания можно сформулировать к ним из из известных нам? (все задания при этом относятся к необходимому уровню).
Учитель предлагает выполнить перечисленные учениками задания и оценить свою работу, используя алгоритм самооценки.
.
Какие основные алгоритмы Вам понадобились, чтобы выполнить задания?
Выполните задание: расставьте в правильном порядке предложения. | Учащиеся отвечают на вопросы учителя (дроби- неправильные смешанные, с разными знаменателями)
Ученики поочерёдно придумывают задания: 1.Сократить неправильную дробь и записать её в виде смешанной дроби. 2.Записать смешанную дробь в виде неправильной дроби. 3.Сравнить дроби и т.д.
Ученики выполняют задания.
Ученики вступают в диалог с учителем: Как привести дробь к новому знаменателю. Как смешанную дробь записать в виде неправильной дроби. Как неправильную дробь записать в виде смешанной дроби. Что значить сократить дробь.
Учащиеся создают знакомые алгоритмы, расставляя предложения в правильном порядке. Учащиеся выставляю себе соответствующие баллы в соответствии с критериями оценивания.
| На доске выписаны дроби. Слайд 5.
На интерактивной доске высвечиваются задания и после их выполнения появляются верные ответы для самооценки учащихся. Слайд 6.
Алгоритм записан на доске для запоминания его учащимися. Слайд 7.
Учащимся раздаются разрезные алгоритмы .Алгоритм приведения дробей к общему знаменателю показывается на доске . Слайд 8. |
| Создание проблемной ситуации | Ребята, теперь выполните моё задание. Задание: сложите дроби (в основе выполнения лежит и неизученный пока алгоритм сложения смешанных дробей) 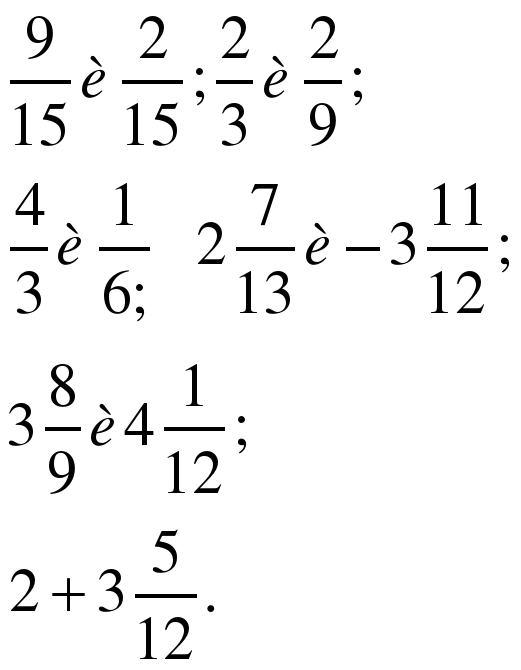
| Учащиеся у доски и в тетрадях выполняют сложение дробей, пытаясь получить правильные ответы, приходят к выводу, что в некоторых примерах они не могут найти ответ. |
|
| Формулирование проблемы (темы и целей урока) | Можно ли выполнить полностью задание?
Какой у вас возник вопрос? Какая же будет тема урока?
Сформулируйте предметную цель:
Может быть кто-то уже понял, как складывают смешанные дроби? Какие есть идеи? Итак, что нам надо чтобы решить проблему? | Диалог: нет, не знаем алгоритм сложения смешанных дробей.
Как сложить смешанные дроби?
Формулируют тему урока: Сложение смешанных дробей. Формулируют цели: -создать алгоритм сложения дробей; -научиться применять алгоритм. Учащиеся предполагают, что сложение смешанных дробей выполняется на основании свойств сложения. Формулируют свой алгоритм сложения смешанных дробей. |
Проблема и тема урока сопровождается записью на интерактивной доске. Слайд 9-11 |
| Открытие нового знания | Учитель просит обратиться к материалам учебника. Через сравнительный анализ представленных там моделей, побуждает учащихся сформулировать новый алгоритм действий. | Самостоятельно читают учебник и работают с модулем, сверяют свои формулировки и выводят окончательную ( стр. 106-107 учебника) | Учебник: математика 5 класс:учеб. Для общеобразоват. Учреждений:/ С.А. Козлова, А.Г. Рубин: Баласс, 2012 (общеобразовательная система 2Школа 2100) |
| Формулирование нового знания | Просит детей самостоятельно заполнить пропуски в предложениях, чтобы получился алгоритм сложения смешанных дробей.
| Самостоятельно выполняют задание, сверяют свои формулировки с формулировкой учебника, выводят окончательную. Выделяют ключивое слово. | Задание на интерактивной доске: заполни пропуски. Слайд 12, 13. |
| Физ.минутка | А теперь немного отдохнём. | Выполняют зарядку | Интерактивная доска. |
| Первичное применение нового | Хорошо, что теперь будем делать?
Просит самостоятельно выполнить задание:№8 стр. 109. | Ученики ставят цель: развивать умение складывать смешанные дроби. Работают в парах: самостоятельно работают с учебником, объясняют задание, формулируя при этом необходимый алгоритм действия. | Учебник. |
| Первичное применение нового | Просит детей выполнить задание: Выполните сложение чисел в пирамиде и дойдя до вершины ( по вариантам) | Учащиеся выбегают к доске и записывают ответы в соответствующие ячейки. | С помощью пера записывают ответы на интерактивной доске. |
| Самостоятельная работа | Просит детей самостоятельно выполнить задание в учебнике, основанное на применении нового знания. Предлагает работу в парах. После выполнения заданий выполняется самооценка: 1. Какое было задание? 2. Удалось выполнить задание? 3. Задание выполнено верно или с ошибками? 4. Какое умение развивали при выполнении задания? 5. Определи отметку, которую ты можешь себе поставить.
| Самостоятельно выполняют задание №8 стр 109, затем решение одной или двух пар учащихся выносится на доску и обсуждается всем классом, при этом анализируются допущенные ошибки
Самооценка двух-трёх пар заслушивается всем классом( договариваются кто отвечает, а кто дополняет ответ) | Интерактивная доска Слайд 14. |
| Повторение и закрепление изученного ранее | Выполнить задачу № 26 (повышенный уровень) | Работают по заданию учителя | Учебник, интерактивная доска, проектор. Слайд 15. |
| Итог урока | Какую проблему решали на уроке?
Над чем надо ещё поработать? | Самостоятельно определяют чего достигли на уроке, отвечая на вопросы: Я знаю; Я запомнил; Я смог.
| Проектор. Слайд 16. |
| Домашнее задание | Учитель называет задания для домашней работы, называя обязательные (инвариант) и какие можно взять на выбор (вариантная часть) стр.112. № 29, 33(а,б) | Определяют для себя инвариантную и вариантную часть задания. | Учебник |