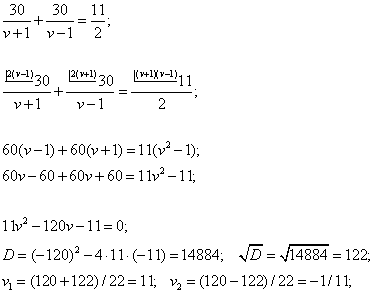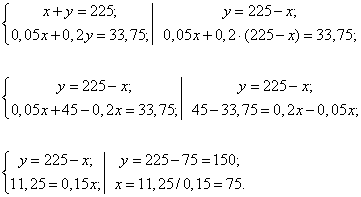Часть B единого государственного экзамена содержит текстовые задачи, в частности, задачи на движение.
В большинстве задач на движение используется формула s = vt, где v – это скорость движения, t – время движения, s – длина пройденного пути. При этом надо учитывать, что указанные величины должны быть в одной системе единиц. Из данной формулы можно получить еще две: v = s/t, t = s/v. Если в задаче говорится о нескольких движущихся объектах, то формулы следует записать для каждого.
Если в явном виде заданы не все величины, часть из них дана в сравнении (меньше – больше, позже – раньше и т.п.), то используя эти сравнения, можно записать соответствующие уравнения. Как правило, число уравнений совпадает с числом сравнений, содержащихся в условии задачи.
Решить задачу можно с помощью системы уравнений, а можно с помощью одного уравнения. Рассмотрим несколько примеров задач на движение по дороге и на движение по воде.
Движение по дороге
Задача 1.
Из города А в город В одновременно выехали два автомобилиста. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути – со скоростью 90 км/ч, в результате чего прибыл в В одновременно с первым автомобилистом. Найдите скорость первого автомобилиста, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
Решение.
При решения текстовых задач эффективно построение схем и составление таблиц.
Используя сравнение скоростей, указанное в задаче, и обозначая скорость первого автомобилиста v, запишем скорость второго автомобилиста на протяжении всего пути: первую половину пути он прошел со скоростью (v – 15) км/ч, а вторую половину со скоростью 90 км/ч.
Таблица будет иметь такой вид:
| Объект | Путь, км | Скорость, км/ч | Время, ч |
| Автомобилист 1 | S | v | t |
| Автомобилист 2 | S | I половина пути v – 15
II половина пути 90 | t |
Условие, что автомобилисты прибыли в пункт назначения одновременно, используем для составления уравнения. Выражаем время первого автомобилиста, которое он затратил на весь путь через S и v: S/v, время второго (учитывая, что первую и вторую половину пути он проезжал с разной скоростью) 1/2S/(v – 15) + 1/2S/90, и приравниваем их. Получаем уравнение относительно скорости первого автомобилиста:
S/v = 1/2S / (v – 15) + 1/2S/90.
Сокращаем его на множитель S ≠ 0 и умножаем обе части уравнения на 2. В результате получаем
2/v = 1/(v – 15) + 1/90.
Для решения последнего уравнения умножаем обе его части на произведение 90v(v – 15) ≠ 0. После всех преобразований получаем квадратное уравнение:
v2 – 105v + 2700 = 0.
Откуда v1 = 60, v2 = 45. Условию задачи (v 54 км/ч) удовлетворяет только корень v1 = 60, следовательно, скорость первого автомобилиста 60 км/ч.
Ответ: 60 км/ч.
Решая задачи на движение, полезно выяснитьсколько раз в условии задачи сравниваются однородные величины. В нашей задаче два сравнения: скоростей автомобилистов и времени их движения на одном и том же пути. Первое сравнение используем для выражения одной скорости через другую. Итоговое уравнение – это сравнение времени движения автомобилистов.
Задача 2.
Велосипедист и пешеход вышли из пунктов А и В, расстояние между которыми 12 км, и встретились через 20 мин. Пешеход прибыл в пункт А на 1ч 36 мин позже, чем велосипедист в пункт В. Найти скорость пешехода. Ответ дайте в км/ч.
Решение.
Из первого условия задачи найдем зависимость между скоростями велосипедиста и пешехода. Пусть v1 – скорость пешехода, v2 – скорость велосипедиста. Тогда 20/60(v1 + v2) = 12, откуда v1 + v2 = 36. Заполним таблицу, принимая за х км/ч скорость пешехода, тогда скорость велосипедиста (36 – х) км/ч.
| Объект | Путь, км | Скорость, км/ч | Время, ч |
| Велосипедист | 12 | 36 – х | 12/(36 – х) |
| Пешеход | 12 | х | 12/х |
Сравнение, что пешеход прибыл в пункт А на 1ч 36 мин позже, чем велосипедист в пункт В, используем для составления уравнения
12/x – 12/(36 – x) = 1 – 36/60.
Откуда получаем квадратное уравнения 1,6x2 – 81,6x + 432 = 0, корни которого х1 = 45, х2 = 6. Так как х – скорость пешехода, следовательно, подходит только х = 6. Скорость пешехода 6 км/ч.
Ответ: 6 км/ч.
Движение по реке
Особенность движения по реке состоит в том, что течение реки увеличивает или уменьшает скорость плывущего объекта. Это изменение равно скорости течения.
Задача 3.
Теплоход проходит по течению реки до пункта назначения 384 км и после стоянки возвращается в пункт отправления. Найдите скорость теплохода в неподвижной воде, если скорость течения равна 4 км/ч, стоянка длится 8 часов, а в пункт отправления теплоход возвращается через 48 часов после отплытия из него. Ответ дайте в км/ч.
Решение.
Обозначим буквой х – скорость теплохода. Скорость течения (4 км/ч) дает возможность выразить скорость теплохода по течению (х + 4) км/ч и против течения (х – 4) км/ч. Заполним таблицу:
| Направление | Путь, км | Скорость, км/ч | Время, ч |
| По течению | 384 | х + 4 | 384/(х + 4) |
| Против течения | 384 | х – 4 | 384/(х – 4) |
Общее время, затраченное на путь туда и обратно, составляет 48 – 8 = 40 часов. Это условие и есть ключевым для составления уравнения
384/(x + 4) + 384/(x – 4) = 40.
После сокращения на 8 уравнение принимает вид
48/(x + 4) + 48/(x – 4) = 5.
Откуда получаем квадратное уравнение 5x2 – 96x – 80 = 0, положительным корнем которого является х = 20. Значит, скорость теплохода в неподвижной воде составляет 20 км/ч.
Ответ: 20 км/ч.
В демонстрационном варианте профильного уровня ЕГЭ 2015 года эти задачи могут встретиться под номером 13.
Рекомендую начинать решение таких задач с краткой записи их условия. И ни в коем случае не спешите смотреть ответы и решения раньше, чем успеете сами подумать о них. Возможны разные способы решения, и не факт, что Ваш способ намного хуже моего.
Задачи с участием водного транспорта.
Такие задачи очень часто сводятся к решению квадратного уравнения. Повторите его.
Задача 1
Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Решение
Cкорость яхты в неподвижной воде обозначим символом v.
Плот движется со скоростью течения реки (2 км/ч), поэтому легко вычислить, за сколько времени плот прошел 24 км: 24/2 = 12 часов.
Яхта отправилась на час позже, значит она была в пути 12 - 1 = 11 часов. За это время она проследовала из пункта A в пункт В по течению реки со скоростью v + 2 км/ч, затратив на это 120/(v + 2) часов, и обратно - против течения со скоростью v - 2 км/ч, затратив на возвращение 120/(v - 2) часов.
Приравнивая сумму времен на путь туда и обратно общему времени в пути, составляем уравнение и решаем его.
Отрицательный корень уравнения в качестве скорости яхты не имеет смысла, поэтомуv = 22 км/ч.
Ответ: 22
Закрыть окно. 
Задача 2
Моторная лодка в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа 30 минут, лодка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость лодки, если известно, что скорость течения реки 1 км/ч.
Решение
Обозначим символом v км/ч собственную скорость лодки. Тогда скорость лодки по течению реки составляет v + 1 км/ч, на обратном пути v - 1 км/ч.
Расстояние между пунктами нам известно. Определим время в пути по течению реки 30/(v + 1) часов и время в пути против течения 30/(v - 1) часов. Сложив эти времена, можем узнать общее время движения лодки.
С другой стороны, нам известны начальный и конечный моменты всей поезки, можем определить её длительность. Всего поездка длилась 18 - 10 = 8 часов. Из них 2 часа 30 минут = 2,5 часа лодка была на стоянке в пункте В, значит всего в движении 8 - 2,5 = 5,5 часов.
Приравнивая эти времена, составляем уравнение и решаем его. Так как в уравнении присутствуют дроби, то число 5,5 тоже удобнее записать в виде обыкновенной дроби 11/2.
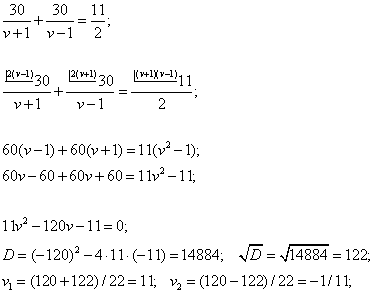
Отрицательный корень уравнения в качестве скорости лодки не имеет смысла, поэтому v = 11 км/ч.
Ответ: 11
Закрыть окно.
Задача 3
Пристани A и B расположены на озере, расстояние между ними равно 390 км. Баржа отправилась с постоянной скоростью из A в B. На следующий день она отправилась обратно со скоростью на 3 км/ч больше прежней, сделав по пути остановку на 9 часов. В результате она затратила на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость баржи на пути из A в B. Ответ дайте в км/ч.
Решение
Обозначим символом v км/ч скорость баржи в направлении от А к В. Тогда скорость баржи в обратном направлении равна v + 3 км/ч. От А к В баржа двигалась 390/vчасов, обратно двигалась 390/(v + 3) часов и еще 9 часов стояла, всего на обратный путь ушло 390/(v + 3) + 9 часов. По условию время в пути туда равно времени на обратный путь, поэтому можем приравнять времена, составить и решить уравнение.
Отрицательный корень уравнения в качестве скорости баржи не имеет смысла, поэтому v = 10 км/ч.
Ответ: 10
Замечание: На озере нет скорости течения воды в одном направлении.
Закрыть окно.
В следующей задаче появляется дополнительное "действующее лицо" - время года, поэтому становится удобнее решать не уравнением, а системой уравнений.
Задача 4
Весной катер идёт против течения реки в 12/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 11/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
Решение
Обозначим символом v собственную скорость катера (км/ч), символом x - скорость течения реки весной (км/ч). Тогда скорость течения реки летом составляет (x - 1) км/ч. Имеем
весной: катер идёт против течения со скоростью (v - x), по течению со скоростью (v +x). По условию первая скорость в 12/3 раза меньше, т.е.
(v + x)/(v - x) = 12/3;
летом: катер идёт против течения со скоростью (v - (x - 1)), по течению со скоростью (v + (x - 1)). По условию первая скорость в 11/2 раза меньше, т.е.
(v + (x - 1))/(v - (x - 1)) = 11/2.
Объединяем уравнения в систему и решаем её:
Ответ: 5
Закрыть окно.
Задачи на проценты с уравнениями и без них.
Следующую задачу можно отнести к задачам на сплавы и растворы, а можно считать такой же обычной задачей на проценты, как простые текстовые задачи на проценты. В этот раздел, как я полагаю, она отнесена не за математическую трудность, а за "трудность" понятий "виноград" и "изюм". Не так ли?
Задача 5
Виноград содержит 90% влаги, а изюм - 5%. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Решение
Для получения изюма виноград сушат, т.е. удаляют из него влагу. Влага нам не нужна, нужно остальное!
Способ I.
Этого остального в изюме 100% - 5% = 95%, т.е. 20·0,95 = 19 кг. (95% = 0,95. Часть от числа находим умножением.)
В винограде остального было столько же, 19 кг. (Оно не исчезало и не прирастало при сушке.) По условию задачи остальное в винограде составляло 100% - 90% = 10%. Таким образом 10% = 0,1 составляют 19 кг. Число по его части находим делением: 19/0,1 = 190 кг.
Для получения 20 килограммов изюма потребуется 190 килограммов винограда.
Способ II.
Обозначим вес винограда за x кг. Определим количество не влаги (остального) в винограде: x - x·0,9. Определим количество не влаги (остального) в изюме: 20 - 20·0,05. Это равные количества, поэтому можно составить уравнение
x - x·0,9 = 20 - 20·0,05.
Решаем уравнение: x·(1 - 0,9) = 20 - 1; x·0,1 = 19; x = 19/0,1 = 190.
Ответ: 190
Закрыть окно.
И еще одна простая задача на проценты, подобная тем, которые мы решали в разделе "Простые текстовые задачи".
Задача 6
В 2008 году в городском квартале проживало 40000 человек. В 2009 году, в результате строительства новых домов, число жителей выросло на 8%, а в 2010 году - на 9% по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?
Решение
В 2008 году проживало 100% или 40000 человек, в 2009 году - на 8% больше, т.е. 108%, или 40000·1,08 = 43200 человек.
В 2009 году проживало 100% или 43200 человек, в 2010 году - на 9% больше, т.е. 109%, или 43200·1,09 = 47088 человек.
Ответ: 47088
Закрыть окно.
А теперь сравните следующую и предыдущую задачи. Похожи?
Задача 7
В понедельник акции компании подорожали на некоторое число процентов, а во вторник подешевели на то же самое число процентов. В результате они стали стоить на 4% дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?
Решение
При открытии торгов в понедельник акции стоили 100% или А рублей, до начала торгов во вторник - на х% больше, т.е. (100 + х)% или А·(100 + х)/100 рублей.
При открытии торгов во вторник акции стоили 100% или А·(100 + х)/100 рублей, по окончании торгов во вторник - на х% меньше, т.е. (100 - х)% или (А·(100 +х)/100)·(100 - х)/100 рублей.
С другой стороны,
при открытии торгов в понедельник акции стоили 100% или А рублей, по окончании торгов во вторник - на 4% меньше, т.е. 96% или А·0,96 рублей.
Составляем уравнение для стоимости акций на конец дня вторника:
(А·(100 + х)/100)·(100 - х)/100 = А·0,96.
Обе части уравнения разделим на А и умножим на 1002, получим:
(100 + х)·(100 - х) = 9600.
Таким образом, в уравнении величина А "сократилась", т.е. она не была дана в условии потому, что не влияет на результат решения. Нам А понадобилась только для того, чтобы рассуждать аналогично предыдущей простой задаче.
Итак, решаем уравнение:
1002 - х2 = 9600;
х2 = 10000 - 9600 = 400;
х = 20 (%).
Ответ: 20
Закрыть окно.
Задача 8
Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200000 рублей. Митя внес 14% уставного капитала, Антон - 42000 рублей, Гоша - 0,12 уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1000000 рублей причитается Борису? Ответ дайте в рублях.
Решение
Определим какая часть уставного капитала внесена каждым учредителем. Митя - 14% = 0,14. Антон - 42000/200000 = 0,21. Гоша - 0,12. Борис - 1 − (0,14 + 0,21 + 0,12) = 0,53.
Прибыль делится пропорционально внесенному капиталу. Следовательно, если Борис внес 0,53 части от 200000, то он должен получить также 0,53 части от 1000000. Часть от числа находим умножением 1000000×0,53 = 530000 (рублей).
Ответ: 530000
Закрыть окно.
Задачи на системы линейных уравнений.
Задача 9
Имеется два сплава. Первый содержит 5% никеля, второй - 20% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Решение
Обозначим за х кг массу первого сплава, за y кг массу второго. Соединив сплавы вместе, получили х + y = 225 кг третьего сплава.
При получении третьего сплава также объединили весь никель. В первом сплаве его было х·0,05 кг, во втором было y·0,20 кг, в третьем стало х·0,05 + y·0,20, что по условию задачи составляет 15% от 225 кг, т.е. 225·0,15 кг = 33,75 кг. Таким образом,х·0,05 + y·0,20 = 33,75.Получили два уравнения объединяем их в систему и решаем её.
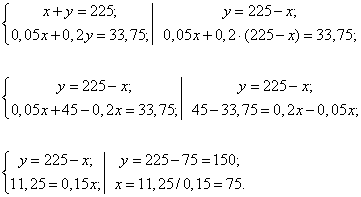
Определили массы обоих сплавов х = 75 кг и y = 150 кг. В ответе требуется записать их разность (на сколько масса первого меньше массы второго), т.е. 150 - 75 = 75 (кг).
Ответ: 75
Закрыть окно.
Одна из главных трудностей при алгебраическом решении текстовых задач состоит в выборе неизвестной величины или величин, которые будут обозначены буквами. Я советую начинать либо с того, что спрашивается в вопросе задачи, либо с того, что содержится в основной формуле, которая описывает процесс. Например, решение задачи на движение основано на применении правила "расстояние = скорость × время". Значит либо расстояние = x, либо время = t, либо скорость = v, смотря что дано, а что неизвестно. При этом, можно получить алгебраические уравнения разного вида. Ведь и "скорость = расстояние : время" и "время = расстояние : скорость". Собственно это варианты одной и той же физической формулы. И от того, в каком варианте вы её раньше вспомните, будет зависеть, как вы введёте обозначения и какие получите уравнения. Здесь не может быть правильного или неправильного начала решения задачи, начните как-нибудь, важно, чтобы было правильным окончание. Однако, решение может оказаться оптимальным и неоптимальным. Вы можете получить слишком громоздкие и сложные уравнения. В этом случае стоит попробовать вернуться к началу задачи и ввести другое обозначение.
Системы уравнений имеет смысл составлять тогда, когда в задаче идет речь о двух или нескольких объектах, на которые одновременно действуют два или несколько факторов, накладывается два или несколько совместимых условий и т.п. Таких ситуаций много в быту, в технике и, особенно много, в экономике. Те из вас, кто собирается продолжать образование, еще не раз столкнутся с системами из разного количества уравнений с разным количеством неизвестных. На экзамене, как правило, вы будете составлять и решать системы из двух уравнений с двумя неизвестными.
Задачи на объезд, обгон и встречное движение.
Когда мы решаем на уроке математики задачи на движение, мы редко вспоминаем о том, что все формулы относятся к описанию движения материальной точки. Происходит это потому, что движущийся объект, как правило, очень мал по сравнению с расстоянием, которое он проходит. Например, поезд, который следует из Москвы в Тюмень всего лишь точка на карте России. Но поезд, который едет по железной дороге в то время, когда мы стоим на переезде и ждем его, вовсе не точка. Его проезд вдоль закрытого шлагбаума занимает порой значительное время. Можно ли в этом случае применять те же формулы? Давайте заглянем в учебник физики, раздел механика. Ответ: можно, если не требуется учитывать вращение или деформирование движущегося объекта. Как применять? Записать их для некоторой точки этого объекта, чаще всего, для центра тяжести. Однако это необязательно, можно выбрать любую точку, которая неподвижна относительно самого объекта.
Итак, чтобы решать задачи на поступательное движение с протяженным объектом, ставим на нём точку в удобном месте, затем чертим схему, на которой отмечаем положение этой точки в заданные моменты времени. И не забываем перейти к одинаковым единицам измерения.
В следующих задачах с поездами, точку я ставила в самом начале - "на носу" поезда. Схему рисовала на нижней линии, а выше рисунки, которые её поясняют.
Задача 10
Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах.
Решение
1) Время дано в секундах, длину проезда нужно найти в метрах, поэтому выразим скорость в м/c. Умножим на 1000, чтобы перейти от километров к метрам, и дважды разделим на 60, чтобы перевести часы в минуты, а минуты в секунды: 80 км/ч = 80·1000/60/60 = 800/36 м/с.
2) Ставим красную точку "на носу" поезда. Чертим схему, на которой отмечаем положение этой точки, когда поезд только начал движение мимо столба, и положение этой точки через 36 секунд, когда поезд проехал мимо столба.
3) По схеме видно, что точка прошла расстояние AB. Известно время (36 с), известна скорость (800/36 м/с), можем найти это расстояние.
AB = (800/36)·36 = 800 (м).
4) Из рисунка видно, что это расстояние совпадает с длиной поезда.
Ответ: 800
Замечание: иногда лучше не производить до конца деление в промежуточных выкладках, потому что в конце дробь может легко сократиться, как это получилось здесь с числом 36.
Задача 11
Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение
1) Время дано в минутах, длину проезда нужно найти в метрах, поэтому выразим скорость в м/мин: 60 км/ч = 60·1000/60 м/мин = 1000 м/мин.
2) Ставим красную точку "на носу" поезда. Чертим схему, на которой отмечаем положение этой точки, когда поезд начал движение мимо лесополосы, и положение этой точки через минуту, когда поезд только что проехал её полностью.
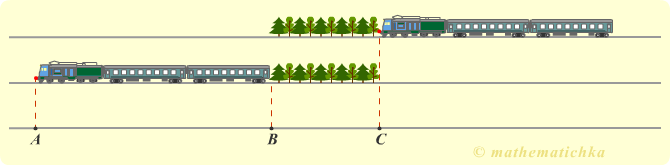
3) По схеме видно, что точка прошла расстояние AС. Известно время (1 мин), известна скорость (1000 м/мин), можем найти это расстояние: AC = 1000·1 = 1000 (м).
4) Из рисунка видно, что это расстояние состоит из двух частей - отрезок AВ равен длине поезда и отрезок ВС равен длине лесополосы.
Находим AВ = AC − BC = 1000 − 400 = 600 (м).
Ответ: 600
Задача 12
По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение
1) Время дано в минутах, ответ нужно дать в метрах, поэтому выражаем обе скорости в м/мин: 90 км/ч = 90·1000/60 = 1500 м/мин; 30 км/ч = 30·1000/60 = 500 м/мин.
2) Ставим красную точку "на носу" пассажирского поезда, и фиолетовую точку "на носу" товарного поезда. Чертим схему, на которой отмечаем положение обоих точек в момент, когда пассажирский поезд догнал товарный, и их положение через минуту, когда пассажирский поезд закончил обгон товарного.
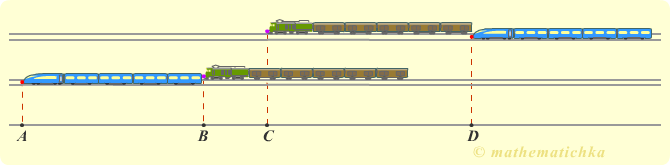
3) По схеме видно, что красная точка прошла расстояние AD за 1 минуту со скоростью 1500 м/мин, следовательно AD = 1500·1 = 1500 (м). Аналогично, фиолетовая точка прошла расстояниеBС за 1 минуту со скоростью 500 м/мин, следовательно BC = 500·1 = 500 (м).
4) Из рисунка видно, что AD = AB + ВС + CD, где отрезок AВ равен длине пассажирского поезда, отрезок СD равен длине товарного поезда.
Находим длину пассажирского поезда AВ = AD − BC − CD = 1500 − 500 − 600 = 400 (м).
Ответ: 400
Задача 13
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
1) Время дано в секундах, ответ нужно дать в метрах, поэтому выражаем обе скорости в м/с: 65 км/ч = 65·1000/60/60 м/с = 650/36 м/с; 35 км/ч = 35·1000/60/60 м/с = 350/36 м/с.
2) Ставим красную точку "на носу" скорого поезда и фиолетовую точку "на носу" пассажирского поезда. Чертим схему, на которой отмечаем положение обоих точек в момент, когда поезда встретились, и их положение через 36 секунд, когда они прошли друг друга.
3) По схеме видно, что фиолетовая точка прошла расстояние AB = (350/36)·36 = 350 метров, a красная точка прошла расстояние BD = (650/36)·36 = 650 метров.
4) Из рисунка видно, что сумма пройденных расстояний - отрезок AD - равна общей длине двух поездов. Найдем длину скорого поезда:
СD = AB + BD − AC = 350 + 650 − 700 = 300 (метров).
Ответ: 300
Для тех из вас, кто знает, что такое относительная скорость, и не боится элементов физики в математических задачах, напоминаю, что существует приём, позволяющий заметно упростить решение задач на объезд, обгон и встречное движение. Нужно один объект "остановить", а скорость другого увеличить на величину скорости первого, если они движутся навстречу друг другу, или, соответственно, уменьшить, если оба движутся в одном направлении. Ниже приведено решение задач 12 и 13 этим способом.
Решение способом II для задачи 12.
Рассмотрим движение пассажирского поезда относительно товарного. Тогда товарный поезд "стоит", а пассажирский едет со скоростью 90 - 30 = 60 км/ч = 1000 м/мин. С этой скоростью за 1 минуту он проезжает расстояние 1000 м, равное длине товарного поезда плюс его собственная длина. (См. картинку к задаче 11 про лесополосу, в качестве которой теперь выступает "стоящий" товарный поезд.) Следовательно, его собственная длина = 1000 - 600 = 400 м.
Ответ: 400.
Решение способом II для задачи 13.
Рассмотрим движение скорого поезда относительно пассажирского. Тогда пассажирский поезд "стоит", а скорый едет со скоростью 65 + 35 = 100 км/ч = 100×1000/3600 = 1000/36 м/c. С этой скоростью за 36 секунд он проезжает расстояние 1000 м, равное длине пассажирского поезда плюс его собственная длина. (См. картинку к задаче 11 про лесополосу, в качестве которой теперь выступает "стоящий" пассажирский поезд.) Следовательно, его собственная длина = 1000 - 700 = 300 м.
Ответ: 300.
Какой способ лучше - судить вам. Но сначала попробуйте самостоятельно решить следующую задачу.
Задача 14
По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 120 метров, второй - длиной 80 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 400 метров. Через 12 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 600 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Показать ответ. 
Задачи на среднюю скорость.
Чтобы найти среднее арифметическое нескольких чисел, нужно их сложить и разделить сумму на количество слагаемых. Например, среднее арифметическое чисел 1, 12, 30, 45 равно 22. Но всегда ли на практике нас интересует именно среднее арифметическое? Если 19 учеников сдали экзамен на 5-ку и только один на 2-ку, можно ли считать, что класс в целом успевает посредственно и заслужил среднюю оценку (5 + 2)/2 = 3,5? Не справедливее ли было учесть "вес" 5-ки и 2-ки? В данном случае это можно сделать, сложив все оценки всех учеников и разделив сумму на число учеников в классе: (19×5 + 1×2)/20 = 4,85. Вполне достойный результат.
Итак, средняя величина и среднее арифметическое чисел, характеризующих эту величину, не одно и то же.
Средняя скорость движения на участке пути длиной S, пройденном за время t, определяется по формуле v = S/t.
Например, если автомобиль двигался 3 часа со скоростью 100 км/ч и 1 час со скоростью 10 км/ч, то за 4 часа он проехал расстояние S = 100×3 + 10×1 = 310 (км). Значит его средняя скорость составляла 310/4 = 77,5 км/ч. А если автомобиль двигался 3 часа со скоростью 10 км/ч и 1 час со скоростью 100 км/ч, то за 4 часа он проехал расстояние S = 10×3 + 100×1 = 130 (км), и его средняя скорость составляла 130/4 = 32,5 км/ч.
Для сравнения вычислим среднее арифметическое значение: (110 + 10)/2 = 55 (км/ч). В первом случае автомобиль большую часть времени ехал быстро, поэтому его средняя скорость больше среднего арифметического значения, а во втором - большую часть времени медленно, поэтому средняя скорость меньше среднего арифметического.
Рассмотрим еще два случая.
Пусть автомобиль двигался 2 часа со скоростью 100 км/ч и 2 часа со скоростью 10 км/ч, тогда за 4 часа он проехал расстояние S = 100×2 + 10×2 = 220 (км). Значит его средняя скорость составляла 220/4 = 55 км/ч, что совпадает со средним арифметическим значением. Так получилось потому, что вклад быстрого и медленного движения был одинаковым по времени.
И, наконец, пусть автомобиль двигался первые 110 км со скоростью 100 км/ч, а следующие 110 км со скоростью 10 км/ч, в итоге на первую половину пути он потратил 110/100 = 1,1 часа, а на вторую - 110/10 = 11 часов. Тогда весь путь 220 км он проехал за 1,1 + 11 = 12,1 часа со средней скоростью 220/12,1 = 18,18182 км/ч, что снова сильно отличается от среднего арифметического значения. Так получилось потому, что вклад быстрого и медленного движения был разным по времени, хотя и одинаковым по длине пройденных участков.
Задача 15
Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час - со скоростью 100 км/ч, а затем два часа - со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение
Всего в пути автомобиль был 2 + 1 + 2 = 5 часов. Проехал расстояние 50·2 + 100·1 + 75·2 = 350 километров. Средняя скорость 350/5 = 70 км/ч.
Ответ: 70
Закрыть окно.
Задача 16
Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км - со скоростью 90 км/ч, а затем 170 км - со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение
Всего автомобиль проделал путь длиной 190 + 180 + 170 = 540 км. Первый участок проехал за 190/50 = 3,8 часа, второй - за 180/90 = 2 часа, третий - за 170/100 = 1,7 часа. Всего был в пути 3,8 + 2 + 1,7 = 7,5 часа. Средняя скорость 540/7,5 = 72 км/ч.
Ответ: 72
Закрыть окно.
Задача 17
Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть - со скоростью 120 км/ч, а последнюю - со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.
Решение
Пусть длина всей трассы S км, а каждого участка, соответственно, S/3 км. Определим время движения по каждому участку:
t1 = (S/3)/60 ч, t2 = (S/3)/120 ч, t3 = (S/3)/110 ч. Время движения по всей трассе
t = t1 + t2 + t3 = (S/3)/60 + (S/3)/120 + (S/3)/110 = (S/3)·(1/60 + 1/120 + 1/110) = (S/3)·(22 + 11 + 12)/1320 = (S/3)·(45/1320) = S·(15/1320) = S/88 (ч).
Средняя скорость v = S/t = S/(S/88) = 88 км/ч.
Ответ: 88
Закрыть окно.
Задачи на производительность.
Производительность труда - эффективность труда в процессе производства. Измеряется количеством продукции, произведенной в единицу времени, или количеством времени, затраченного на производство единицы продукции.
Производительность оборудования - объём продукции (работы), производимой в единицу времени данным оборудованием. Измеряется в тоннах, штуках, метрах и т.п. на единицу времени.
В любом случае к задачам на производительность, надо относиться так же, как к задачам на движение с заданной (или искомой) скоростью, так как
Производительность, проще говоря, это скорость производства:
- скорость движения = расстояние/время;
- производительность труда = объем продукции/время;
- производительность "трубы" = объем воды/время; и т.п.
Просто, читая условие задачи, нужно помнить, что трубы, насосы, станки ... - это оборудование, подготовка к экзамену, выполнение заказа, покраска забора ... - это труд.
Задача 18
Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?
Решение
Способ I.
Весь заказ обозначим символом Z, время, которое рабочие работали вместе обозначим символом t. Каждый из двух рабочих работает со скоростью Z/15. За 3 часа первый рабочий выполнил (Z/15)·3 заказа, еще за t часов оба рабочих выполнили (Z/15)·t·2 заказа. Таким образом, был выполнени весь заказ, т.е. (Z/15)·3 + (Z/15)·t·2 =Z.
Умножаем обе части уравнения на 15 и делим на Z. Получим
3 + t·2 = 15; t·2 = 12; t = 6.
Таким образом, на выполнение всего завказа потребовалось 3 + t = 3 + 6 = 9 часов.
Способ II.
Каждый из двух рабочих за час выполняет 1/15 часть заказа. За 3 часа первый рабочий выполнил 3·(1/15) = 3/15 = 1/5 часть заказа. Оставшиеся 1 - 1/5 = 4/5 части заказа рабочие делали вместе со скоростью 2·(1/15) = 2/15 части в час, следовательно выполнили эту работу за время (4/5)/(2/15) = (4·15)/(5·2) = 6 часов. Таким образом, весь заказ был выполнен за 3 + 6 = 9 часов.
Ответ: 9
Замечание: Способ II, на мой взгляд, лучше. Но, если вы за то время, которое занимались алгеброй, забыли арифметику, вводите дополнительную неизвестную величину - весь объем продукции или работы. После составления уравнения эта величина должна сократиться.
Закрыть окно.
Задача 19
Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 8 вопросов теста, а Ваня - на 9. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 20 минут. Сколько вопросов содержит тест?
Решение
Пусть тест содержит х вопросов. Петя ответил за х/8 часов. Ваня ответил за х/9 часов. Петя закончил свой тест позже Вани на х/8 - х/9 часов или на (х/8 - х/9)·60 минут, что по условию задачи составило 20 минут:
(х/8 - х/9)·60 = 20;
х·(1/8 - 1/9)·3 = 1;
х·(3/8 - 1/3) = 1; х·(9 - 8)/24 = 1; х = 24.
Ответ: 24
Закрыть окно.
Задача 20
Первый насос наполняет бак за 20 минут, второй - за 30 минут, а третий - за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Решение
В вопросе задачи время в минутах, поэтому везде перейдем к минутам. 1 час = 60 мин.
Способ I.
Объём бака обозначим символом V литров, тогда первый насос работает со скоростьюV/20 л/мин, второй - со скоростью V/30 л/мин и третий - со скоростью V/60 л/мин. Работая одновременно, они наполняют бак со скоростью V/20 + V/30 + V/60 = V·(1/20 + 1/30 + 1/60) = V·(3 + 2 + 1)/60 = V·0,1 (л/мин). Значит весь бак будет наполнен заV/(V·0,1) = 10 минут.
Способ II.
Первый насос наполняет за минуту 1/20 часть бака, второй - 1/30 часть и третий - 1/60 часть. Работая одновременно, они наполняют за минуту 1/20 + 1/30 + 1/60 = 6/60 = 1/10 часть бака. Значит весь бак будет наполнен за 10 минут.
Ответ: 10
Закрыть окно.
Задача 21
Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?
Решение
Пусть вторая труба наполняет резервуар за t минут, тогда за одну минуту она наполняет 1/t часть резервуара. Первая труба наполняет резервуар дольше, за t + 6 минут, а за минуту она наполняет 1/(t+6) часть резервуара. Обе трубы вместе за минуту наполняют 1/t + 1/(t+6) часть резервуара. С другой стороны, они вместе наполняют резервуар за 4 минуты, значит за минуту - 1/4 часть. Составим и решим уравнение:
1/t + 1/(t+6) = 1/4; 4(t+6) + 4t = t(t+6); 8t + 24 = t2 + 6t;
t2 − 2t − 24 = 0. Корни уравнения t1 = 6; t2 = −4. Отрицательный корень не имеет смысла, следовательно t = 6.
Ответ: 6
Закрыть
