
Трапеция

Цель урока:
- изучение и закрепление нового материала

Задачи:
Образовательная – дать определение трапеции; ознакомить учащихся с видами трапеций.
Развивающая – развить логическое мышление познавательный интерес к предмету.
Воспитательная – воспитать усидчивость, внимательность и аккуратность, добросовестное отношение к предмету.

План урока:
- Организационный момент (1 минута)
- Проверка домашнего задания. Математический диктант (10 минут)
- Объяснение нового материала (14 минут).
- Первичное закрепление нового материала (18 минут)
- Домашнее задание. Итог урока (2 минуты)

Дайте определение средней линии треугольника:
- Отрезок, соединяющий середины двух сторон треугольника называется средней линией.
Сформулируйте теорему о средней линии треугольника:
- Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна её половине.

Математический диктант
1 вариант
2 вариант
задание 1
задание 2
задание 3
задание 4
задание 1
задание 2
задание 3
задание 4

Задание 1 (1 вариант)
Две стороны треугольника соединены отрезком, не параллельным третьей стороне. Служит ли этот отрезок средней линией данного треугольника?

Задание 1 (2 вариант)
Точки A и B являются серединами двух сторон треугольника. Как называется отрезок AB ?

Задание 2 (1 вариант)
Сторона AB треугольника ABC равна . Чему равна средняя линия треугольника, параллельная этой стороне?

Задание 2 ( 2 вариант)
Средняя линия треугольника ABD параллельна стороне BD , рана . Чему равна сторона BD ?

Задание 3 ( 1 вариант)
Точки M , P , O – середины сторон треугольника ABC . Найдите периметр треугольника ABC , если стороны треугольника MPO равны , и 5см.

Задание 3 ( 2 вариант)
Точки A , B , C – середины сторон треугольника MPO . Найдите периметр треугольника ABC , если отрезки MP , MO и PO равны соответственно 3 дм, 4 дм и 5 дм.

Задание 4 ( 1 вариант)
Концы отрезка AB лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны. Обязательно ли отрезок AB – средняя линия этого треугольника?

Задание 4 ( 2 вариант)
Концы отрезка KL лежат на двух сторонах треугольника. Отрезок KL параллелен третьей стороне этого треугольника и равен ¼ части её длины. Служит ли отрезок KL средней линией этого треугольника?
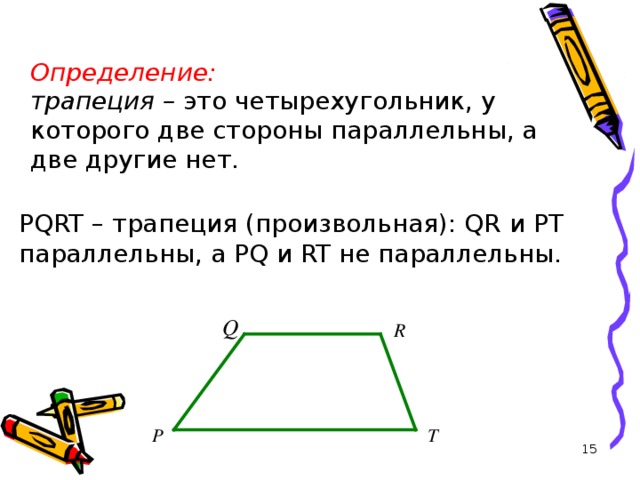
Определение:
трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.
PQRT – трапеция (произвольная): QR и PT параллельны, а PQ и RT не параллельны.
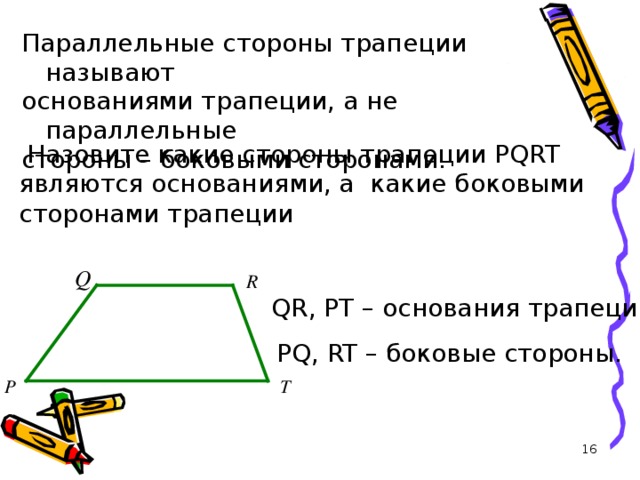
Параллельные стороны трапеции называют
основаниями трапеции, а не параллельные
стороны – боковыми сторонами.
Назовите какие стороны трапеции PQRT являются основаниями, а какие боковыми сторонами трапеции
QR , PT – основания трапеции
PQ , RT – боковые стороны.
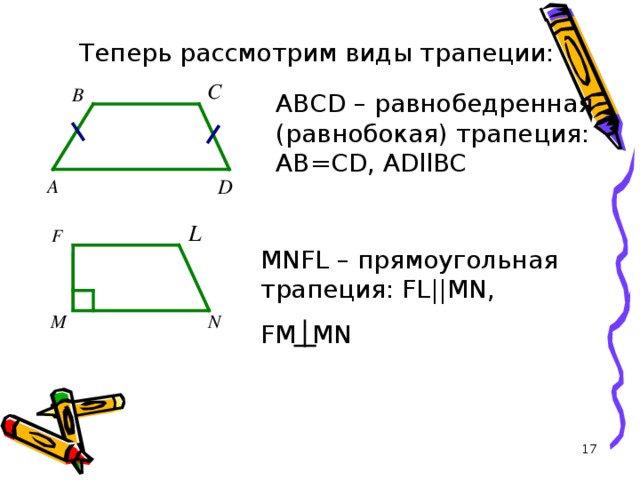
Теперь рассмотрим виды трапеции:
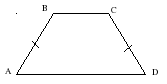
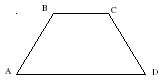
ABCD – равнобедренная (равнобокая) трапеция: АВ= CD, ADllBC
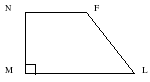
MNFL – прямоугольная трапеция: FL||MN,
FM MN

Решаем в классе :
№ 82
№ 70
 А 1 B 1 || AC и А 1 B 1 = ½AC . б) Рассмотрим ∆ ADC: C 1 D 1 – средняя линия = C 1 D 1 || AC и C 1 D 1 = ½AC . в) Из а) и б) = А 1 B 1 || C 1 D 1 и А 1 B 1 = C 1 D 1 = ½AC = = А 1 B 1 C 1 D 1 - параллелограмм (по признаку пар-ма). Ч. т. д. D" width="640"
А 1 B 1 || AC и А 1 B 1 = ½AC . б) Рассмотрим ∆ ADC: C 1 D 1 – средняя линия = C 1 D 1 || AC и C 1 D 1 = ½AC . в) Из а) и б) = А 1 B 1 || C 1 D 1 и А 1 B 1 = C 1 D 1 = ½AC = = А 1 B 1 C 1 D 1 - параллелограмм (по признаку пар-ма). Ч. т. д. D" width="640"
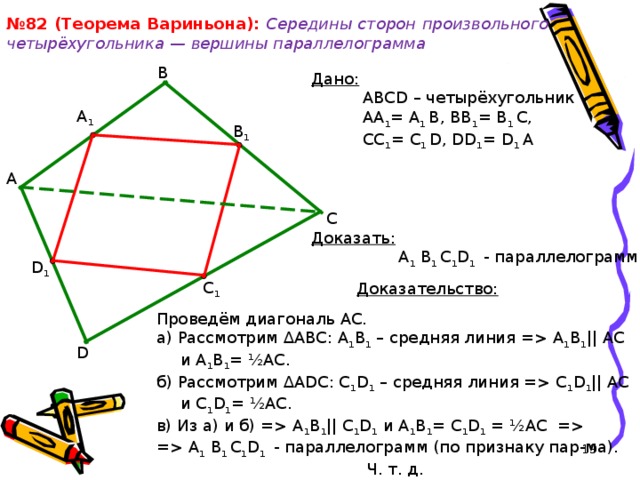
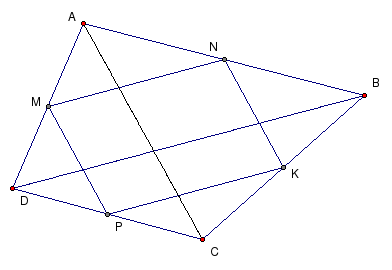
№ 82 (Теорема Вариньона): Середины сторон произвольного четырёхугольника — вершины параллелограмма
B
Дано:
ABCD – четырёхугольник
A А 1 = А 1 B, BB 1 = B 1 C,
CC 1 = C 1 D, DD 1 = D 1 A
Доказать:
А 1 B 1 C 1 D 1 - параллелограмм
А 1
B 1
А
C
D 1
C 1
Доказательство:
Проведём диагональ AC.
а) Рассмотрим ∆ ABC: А 1 B 1 – средняя линия = А 1 B 1 || AC и А 1 B 1 = ½AC .
б) Рассмотрим ∆ ADC: C 1 D 1 – средняя линия = C 1 D 1 || AC и C 1 D 1 = ½AC .
в) Из а) и б) = А 1 B 1 || C 1 D 1 и А 1 B 1 = C 1 D 1 = ½AC =
= А 1 B 1 C 1 D 1 - параллелограмм (по признаку пар-ма).
Ч. т. д.
D
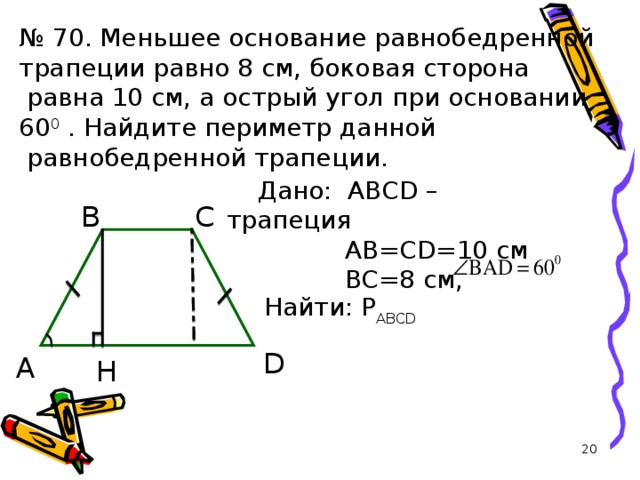
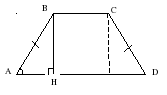
№ 70. Меньшее основание равнобедренной
трапеции равно 8 см, боковая сторона
равна 10 см, а острый угол при основании
60 0 . Найдите периметр данной
равнобедренной трапеции.
Дано: ABCD – трапеция
AB = CD =10 см
BC =8 см ,
B
C
Найти: Р ABCD
D
A
H
19
C
B
D
A
H
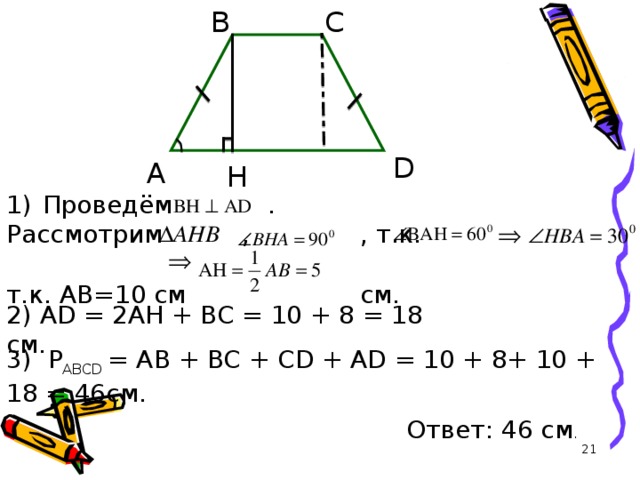
Рассмотрим , , т.к.
т.к. AB =10 см см.
2) AD = 2AH + BC = 10 + 8 = 18 c м .
3) Р ABCD = AB + BC + CD + AD = 10 + 8+ 10 + 18 = 46c м .
Ответ : 46 c м .

Домашнее задание:
№ 68 и теоретический материал






















 А 1 B 1 || AC и А 1 B 1 = ½AC . б) Рассмотрим ∆ ADC: C 1 D 1 – средняя линия = C 1 D 1 || AC и C 1 D 1 = ½AC . в) Из а) и б) = А 1 B 1 || C 1 D 1 и А 1 B 1 = C 1 D 1 = ½AC = = А 1 B 1 C 1 D 1 - параллелограмм (по признаку пар-ма). Ч. т. д. D" width="640"
А 1 B 1 || AC и А 1 B 1 = ½AC . б) Рассмотрим ∆ ADC: C 1 D 1 – средняя линия = C 1 D 1 || AC и C 1 D 1 = ½AC . в) Из а) и б) = А 1 B 1 || C 1 D 1 и А 1 B 1 = C 1 D 1 = ½AC = = А 1 B 1 C 1 D 1 - параллелограмм (по признаку пар-ма). Ч. т. д. D" width="640"



















