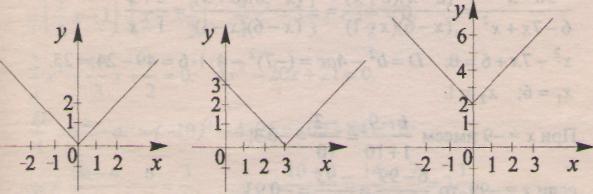РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЁХЧЛЕНА НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ

РАЗЛОЖЕНИЕ КВАДРАТНОГО ТРЁХЧЛЕНА НА ЛИНЕЙНЫЕ МНОЖИТЕЛИ

Урок №1

Цели: доказать теорему о разложении квадратного трёхчлена на множители и закрепить её знание в ходе выполнения упражнений.

Ход урока

I. Проверка домашнего задания.

1. Итоги самостоятельной работы.

2. Двое учащихся работают у доски по карточкам.

Карточка №1

1) Найдите корни квадратного трёхчлена:
7x²-21x+ 14 и 3y²-18.

2) Принадлежит ли графику функции у =126/x точка А (0; -126)?

Карточка № 2

1. Докажите, что при любом у квадратный трёхчлен у² -4у + 1 принимает положительные значения.

2. Решите уравнение - 2х² - 5х +18 = 0.

II. Изучение нового материала.

1. Вспомнить способы разложения многочлена на множители.

2. Разложение на множители квадратного трёхчлена

Зх²-21x+ 30 = = 3(х² - 7х +10) = 3(х² - 2х - 5х +10) = 3(х(х - 2) – 5(х - 2)) =

3(х - 2)(х - 5).

При х = 2 и х = 5 произведение 3(х - 2)(х - 5) , а значит, и трёх­член 3х² -21x + 30 обращаются в нуль. Следовательно, числа 2 и 5 являются его корнями.

1. Доказательство теоремы:

«Если х₁, и х₂ - корни квадратного трёхчлена

aх²+bс + с, то ах² + bх + с = а(х-x_t)(x-х₂)»

4. Разобрать пример 1 и пример 2 на стр. 21-22 в учебнике.

III. Закрепление изученного материала.

1. Решить № 60 (б, в, з, и) на доске и в тетрадях.

2. Решить № 61 (б, г). Применить формулы (a±b)²=-a² ±2ab+b .

б) -9x²+12x-4 = -(9x²-12х + 4) = -(Зх-2)²;

г) 0,25m² - 2т + 4 = 0,25(т² – 8m +16) = 0,25(т -4)².

1. Доказать тождество № 63 (б).

2. Устно № 64. Указание: необходимо вычислить дискриминант

D = b² -4ас.

1. Устно № 71 по рис. 19 в учебнике.

2. Построить графики функций:

y=IxI y=Ix-3I y=IxI+2

IV. Итоги урока.

Домашнее задание: п. 4; решить № 62; 63 (а); 86; 177*.