"Применение подобия на практике"

«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает возможность правильно мыслить и рассуждать». Г. Галилей

Класс: 8

Предмет: геометрия

Цели урока :

Образовательные : повторить признаки подобия треугольников, закрепить признаки при решении задач, рассмотреть применение признаков подобия на практике

Развивающие

• повышать интерес учащихся к геометрии;
• активизировать познавательную деятельность учащихся;
• развивать логическое мышление, творческие способности, математическую речь

Воспитательные

• формировать умение работать в команде;
• воспитание настойчивости в достижении цели

Тип урока : практический семинар по решению задач

Мотивация урока

Геометрические знания широко применяются в жизни – в быту, на производстве, в науке. Прослеживая зарождение и становление геометрии, легко усмотреть её связь с практической деятельностью человека. В наше время задачи по геометрии по-прежнему находят широкое применение в строительстве, искусстве и архитектуре, а также во многих отраслях промышленности. Теперь ученые, используя накопившиеся материалы в области геометрии, совершенствуют их, ищут что-то новое, создают свои гипотезы. А без практики не может существовать и теория. И сегодня я предлагаю вооружившись знаниями геометрии выяснить практическую значимость знаний, которые приобретаются в процессе учёбы в школе. На уроках геометрии мы прошли подобие треугольников. Какими способами с помощью подобия треугольников можно измерять очень большие высоты и недосягаемые расстояния?

1 группа

2 группа

3группа

4 группа

Теоретическая разминка

№ 1

• Какие треугольники называют подобными? (углы равны, стороны пропорциональны)
• Какое из этих слов лишнее и почему? Прямоугольник, ромб, треугольник, квадрат. (Треугольник, все остальные фигуры четырехугольники).
• Первый признак подобия треугольников. (СУС)
• Как называется прямоугольник, у которого все стороны равны?

( квадрат)

• Верно ли, что треугольник со сторонами 3;4;5-прямоугольный? (да, 3 2 +4 2 =5 2 ).
• Чему равно отношение площадей двух подобных треугольников?

( к 2 )

№ 2

• Какие отрезки называются пропорциональными ( отношение длин равны )
• Верно ли, что четырехугольник, у которого противоположные стороны попарно параллельны, называется трапецией? (нет, этот четырехугольник параллелограмм )
• Второй признак подобия треугольников( уу )
• Какое из этих слов лишнее и почему? Биссектриса, высота, диагональ, медиана . ( Диагональ, все остальные принадлежат треугольнику )
• Чему равно отношение периметров подобных треугольников? ( к )

№ 3  

• Как, одним словом назвать сумму длин всех сторон многоугольника? ( периметр )
• Как называется отрезок соединяющий вершину треугольника с серединой противоположной стороны треугольника? ( медиана )
• Третий признак подобия треугольников.( ССС )
• Какое из этих слов лишнее и почему? Пифагор, Фалес, Дискриминант, Виет, . ( Дискриминант )
• Свойство биссектрисы треугольника( делит сторону на отрезки пропорциональные двум другим сторонам )

№ 4.

• Свойство средней линии треугольника.( Соединяет середины двух сторон , параллельна третьей стороне и равна ее половине )
• Свойство медиан треугольника ( точкой пересечения делятся в отношении 2:1 )
• Верно ли утверждение: если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники равны? (нет, треугольники подобны ).
• Какое из этих слов лишнее и почему? Прямоугольник, ромб, трапеция, квадрат. (трапеция )
• Верно ли утверждение: четырехугольник, у которого диагонали взаимно перпендикулярны, является квадратом?( нет, не обязательно, возможно – ромб )

Марафон открытий

1 группа

Применить метод подобия, для измерения или определения высоты дома, дерева

с помощью записной книжки

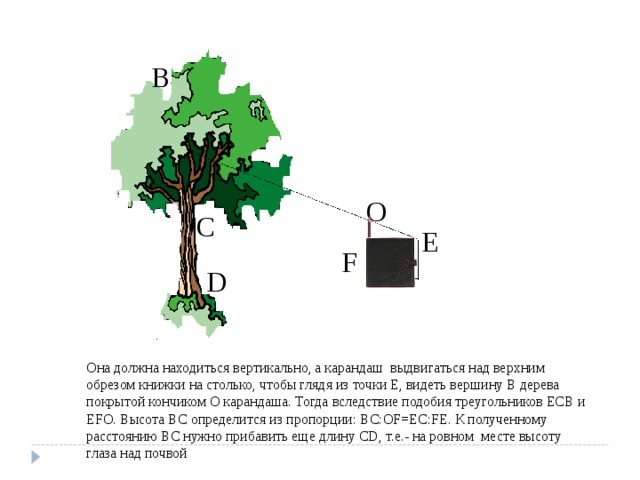
Можно измерить высоту дерева с помощью записной книжки, если она снабжена карандашом, всунутым в петельку при книжке. Она поможет построить вам в пространстве те два подобных треугольника, из которых получается искомая высота. Книжку надо держать возле глаза.

B

O

C

E

F

D

Она должна находиться вертикально, а карандаш выдвигаться над верхним обрезом книжки на столько, чтобы глядя из точки Е, видеть вершину В дерева покрытой кончиком О карандаша. Тогда вследствие подобия треугольников ЕСВ и ЕFО. Высота ВС определится из пропорции: BC:OF=EC:FE. К полученному расстоянию ВС нужно прибавить еще длину CD, т.е.- на ровном месте высоту глаза над почвой

По способу Жюля Верна.

Этот способ описан в книге у Жюля Верна в известном романе

«Таинственный остров». Там инженер и Герберт измеряют высоту

площадки дальнего вида. Я же расскажу этот способ на примере измерения высоты дерева.

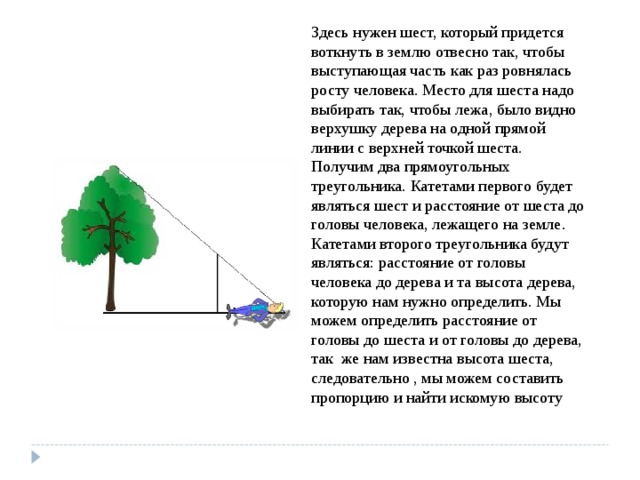
Здесь нужен шест, который придется воткнуть в землю отвесно так, чтобы выступающая часть как раз ровнялась росту человека. Место для шеста надо выбирать так, чтобы лежа, было видно верхушку дерева на одной прямой линии с верхней точкой шеста. Получим два прямоугольных треугольника. Катетами первого будет являться шест и расстояние от шеста до головы человека, лежащего на земле. Катетами второго треугольника будут являться: расстояние от головы человека до дерева и та высота дерева, которую нам нужно определить. Мы можем определить расстояние от головы до шеста и от головы до дерева, так же нам известна высота шеста, следовательно , мы можем составить пропорцию и найти искомую высоту

• 2группа
• С помощью подобия можно найти расстояния,
• которые невозможно измерить.
• С помощью булавочного прибора .
• Например ширину реки.
• АВ это ширина реки. Находим точку С на продолжении АВ с помощью прибора. Держим этот прибор так чтобы смотря вдоль двух булавок, вы видели, как обе они покрывают точки В и А. Затем намечается прямая СD под прямым углом к СА, с помощью этого же прибора. На прямой СD отмечают точки Е и F, так чтобы СЕ было в несколько раз больше ЕF. Затем с булавочным прибором намечают направление FG, перпендикулярное к FC. Теперь идя по прямой FG, отыскивают на этой прямой точку Н, из которой веха Е кажется покрывающей точку А. Получилось, FH во столько раз меньше АС во сколько FE меньше ЕС.

• астролябия (прибор для измерения углов на местности, рулетка и вехи

Пусть в реке есть остров и на нём дерево это точка С. Нужно узнать н каком расстоянии оно находится. Для выполнения данной работы потребуется астролябия (прибор для измерения углов на местности), рулетка вехи.

• Вехи устанавливают в точки А и В и с помощью астролябия измеряют угол 1 и угол 2. Рулеткой измеряют расстояние от точки А до В. На плоскости строят треугольник А1В1С1 с углами равными углу 1 и углу 2, этот треугольник будет подобный треугольнику АВС по первому признаку подобия (УУ), следовательно можно найти сходственные стороны треугольников на плоскости – измерением, а на местности вычислением.

3 группа

Самый легкий и самый древний способ – которым греческий мудрец Фалес за шесть веков до нашей эры определил в Египте высоту пирамиды. Он воспользовался ее тенью. Жрецы и Фараон, собравшиеся у подножья высочайшей пирамиды, озадаченно смотрели на северного пришельца, отгадывающего по тени высоту огромного сооружения. Фалес выбрал день, и час когда его тень равнялась его росту, тогда и высота пирамиды должна соответствовать ее высоте.

А

Таким образом, можно измерить и высоту дерева.

Но этот способ не всегда можно применить. Чтоб не дожидаться когда ваша тень станет равна вашему росту можно поступить проще.

Измерить тень дерева и вашу собственную. Во сколько раз тень дерева больше вашей, значит во столько же раз дерево выше вашего роста. Из этого можем составить пропорцию AB:ED=BC:EF

Это вытекает из геометрического подобия треугольников АВС и DEF.

Но этим способом мы получаем не совсем точные результаты

Вполне возможно обойтись при измерении высоты и без тени Мы можем воспользоваться свойством равнобедренного треугольника. Для этого надо изготовить один простой прибор, его можно изготовить из дощечки и двух булавок. Приближаясь к дереву или отдолясь от него вы всегда найдете такое место А из которого, глядя на булавки E, F вы увидите , что они покрывают

верхушку С дерева: это значит что продолжение гипотенузы ЕF проходит через С. Тогда очевидно расстояние EB равно CB так как угол Е=45.

Следовательно измерив расстояние ЕВ и прибавив ОВ , т.е. возвышение АЕ глаза над землей получите искомую высоту дерева.

4 группа применить метод подобия, для измерения или определения высоты дома, дерева при помощи зеркала

Высоту дерева можно определить при помощи зеркала. На некотором расстоянии от измеряемого дерева на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево АВ во столько раз выше роста наблюдателя ЕD, во сколько раз расстояние ВС от зеркала до дерева больше расстояния СD от зеркала до наблюдателя.

Способ основан на законе отражения света. Вершина А отражается в точке А1 так, что АВ=А1В.

Из подобия же треугольников ВСА1 и СЕD следует, что А1В: УВ=ВС:СD.

В этой пропорции остается лишь заметитьА1В равным

ему АВ, чтобы обосновать указанное в задаче соотношение.

В этой пропорции остается лишь заменить А 1 В равным ему АВ, чтобы обосновать указанное в задаче соотношение.

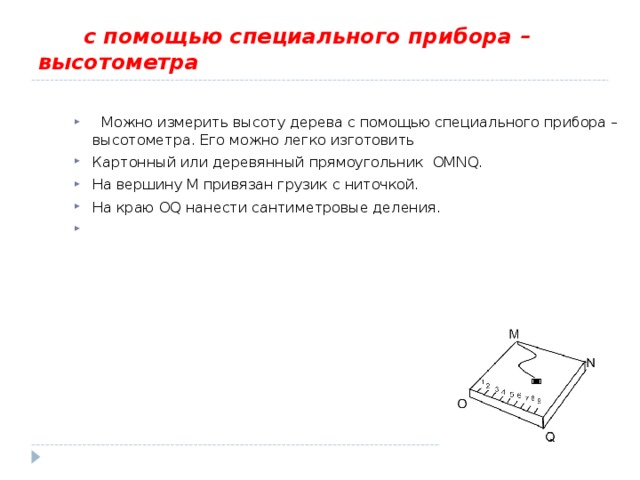
с помощью специального прибора – высотометра

• Можно измерить высоту дерева с помощью специального прибора – высотометра. Его можно легко изготовить
• Картонный или деревянный прямоугольник OMN Q .
• На вершину M привязан грузик с ниточкой.
• На краю О Q нанести сантиметровые деления.
•  

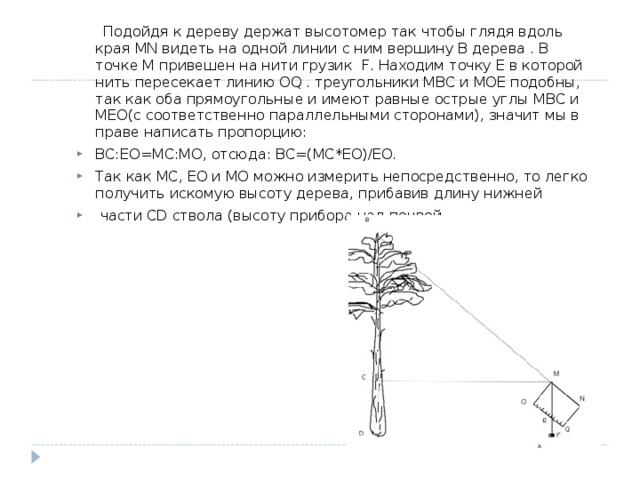
Подойдя к дереву держат высотомер так чтобы глядя вдоль края MN видеть на одной линии с ним вершину В дерева . В точке М привешен на нити грузик F . Находим точку Е в которой нить пересекает линию OQ . треугольники МВС и МОЕ подобны, так как оба прямоугольные и имеют равные острые углы МВС и МЕО(с соответственно параллельными сторонами), значит мы в праве написать пропорцию:  

• ВС:ЕО=МС:МО, отсюда: ВС=(МС*ЕО)/ЕО.
• Так как МС, ЕО и МО можно измерить непосредственно, то легко получить искомую высоту дерева, прибавив длину нижней
• части С D ствола (высоту прибора над почвой.

Практикум

Практическая часть

Измерение высоты многоэтажного дома

Длина тени многоэтажного здания равна 4 м, а длина тени вертикально закрепленного колышка равна 0,1 м. Вычислите высоту здания, если высота колышка равна 0,7 м.

Практическая часть

Измерение высоты дерева

Для измерения высоты дерева человек измерил:

Ширину записной книжки – 10см

Карандаш – 12см

Расстояние от него до дерева – 624см

Уровень глаза над землей – 100м

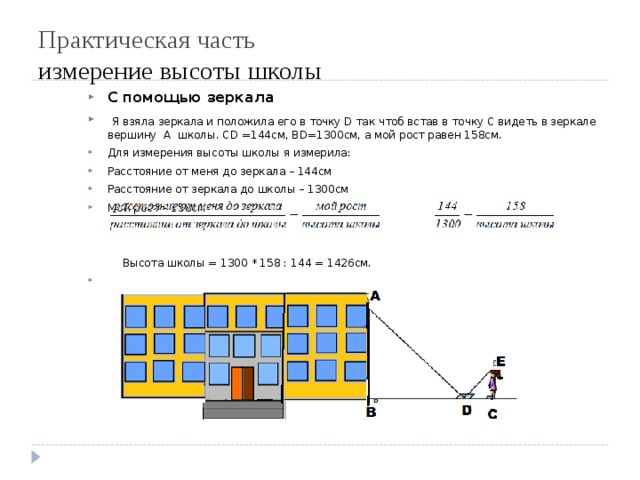
Практическая часть измерение высоты школы

• С помощью зеркала
•   Я взяла зеркала и положила его в точку D так чтоб встав в точку С видеть в зеркале вершину А школы. С D =144см, В D =1300см, а мой рост равен 158см.
• Для измерения высоты школы я измерила:
• Расстояние от меня до зеркала – 144см
• Расстояние от зеркала до школы – 1300см
• Мой рост – 158см

Высота школы = 1300 * 158 : 144 = 1426см.

• Значит высота школы равна 1426см = 14.26м .

Реши, если силен

Определение ширины реки Человек ростом 180 см ( по уровню глаз ) определяет ширину реки. Он втыкает на берегу шест высотой 170 см и отходит от него до тех пор, пока верхушка шеста и противоположный берег реки не окажутся расположенными на одном луче зрения. Отойти ему пришлось на 10 м. Какова ширина реки?

Решение:

Определение высоты предмета

Человек ростом 180 см ( по уровню глаз ) определяет высоту телебашни. Он втыкает в землю шест высотой 350 см и отходит от него до тех пор, пока верхушка шеста и верхушка башни не окажутся расположенными на

одном луче зрения. Отойти ему пришлось на 7 м. Какова высота телебашни, если расстояние от шеста до телебашни равно 630 м?

Решение:

Определение расстояния до недоступной точки

Радиолокационный пост наблюдения находится в 20 км от горы высотой 3 км. Из-за горы на высоте 9 км летит самолёт. На каком расстоянии (по горизонтали) он будет обнаружен?

Решение:

Определение расстояний с помощью монеты На каком расстоянии от наблюдателя находится заводская труба высотой 150 метров, если монета диаметром 15мм , находящаяся на расстоянии вытянутой руки ( 60 см)от глаза, заслоняет эту трубу полностью ?

Решение:

Определение глубины уровня воды колодца.

Человек ростом 2 м определяет глубину уровня воды в колодце шириной

3 м. Он отходит от кромки колодца до тех пор, пока не перестает видеть воду в нем. Отойти пришлось на 1 м. Какова глубина уровня воды?

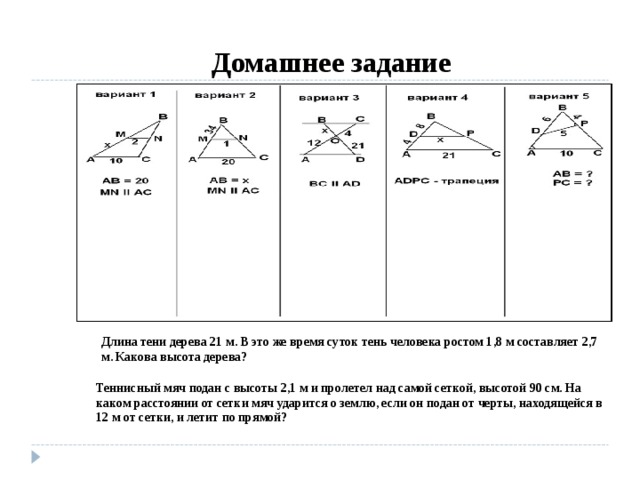
Домашнее задание

Длина тени дерева 21 м. В это же время суток тень человека ростом 1,8 м составляет 2,7 м. Какова высота дерева?

Теннисный мяч подан с высоты 2,1 м и пролетел над самой сеткой, высотой 90 см. На каком расстоянии от сетки мяч ударится о землю, если он подан от черты, находящейся в 12 м от сетки, и летит по прямой?