Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Открытый урок " Умножение положительных и отрицательных чисел"
Тема: Умножение и деление положительных и отрицательных чисел
Цели: (слайд 1) Цели:
Образовательные: отработка умений и навыков при сложении, вычитании, умножении и делении чисел с разными знаками путём применения разнообразных форм упражнений (решении примеров, уравнений, упрощении выражений), научить делить положительные и отрицательные числа
Развивающие: формировать навыки самостоятельной работы; развивать логическое мышление, вычислительные навыки; расширение кругозора.
Воспитательные: воспитание познавательного интереса к предмету; воспитывать культуру труда, математической речи, активность, самостоятельность, культуру общения
Оборудование: ПК, мультимедийный проектор
2. Мотивация урока. Французский писатель 19 столетия Анатоль Франс однажды заметил: «Учиться можно весело… Чтобы переваривать знания, надо поглощать их с аппетитом». Пусть эти слова послужат девизом сегодняшнего урока, урока-путешествия в страну положительных и отрицательных чисел.
Ребята, а что у нас принято на уроке?
А еще сегодня нам на уроке пригодятся:
хорошее настроение;
уважение друг к другу;
знание материала;
желание открыть истину;
добросовестная работа;
осмысление произведенной деятельности.
Едва ли не самым тёмным для учащихся местом в математике является учение о действиях с отрицательными числами. И это не потому, что устанавливаемые правила действий сложны. Напротив, они очень просты. Но тёмными остаются два вопроса: 1) Зачем вводятся отрицательные числа? 2) Почему над ними совершаются действия по таким-то правилам, а не по иным? В частности, очень плохо понимается, почему при умножении и делении отрицательного числа на отрицательное результат есть положительное число.
Все эти вопросы возникают потому, что с отрицательными числами учащихся обычно знакомят до того, как они начали решать уравнения, и больше не возвращаются к правилам действий с отрицательными числами. Между тем лишь в связи с решением уравнений выясняется ответ на оба поставленных выше вопроса. Исторически отрицательные числа возникли именно в этой связи. Не будь уравнений, не было бы нужды и в отрицательных числах.
Долгое время уравнения изучались без помощи отрицательных чисел; при этом возникали многие неудобства; для устранения этих неудобств и были введены отрицательные числа. При этом в течение долгого времени многие выдающиеся математики отказывались вводить их в употребление или вводили с большой неохотой. Ещё Декарт (1596–1650) называл отрицательные числа “ложными числами”.
Таким примерно образом и были введены отрицательные числа; цель этого — рационализация вычислительного процесса; правила действий над отрицательными числами явились результатом введения этого рационализаторского приёма в вычислительную практику.
Многолетние и многообразные испытания показали, что этот приём обладаем огромной эффективностью и находит себе блестящие применения во всех областях науки и техники. Всюду введение отрицательных чисел позволяет охватить единым правилом такие явления, для которых нужно было бы выдумывать десятки правил, если ограничиться числами положительными.
Итак, на два выше поставленных вопроса нужно ответить следующим образом: 1) отрицательные числа вводятся затем, чтобы устранить ряд трудностей, возникших прежде всего при решении уравнений; 2) правила действий над ними вытекают из необходимости согласовать результаты, полученные с помощью отрицательных чисел, с теми результатами, которые могли бы быть получены и без них.
Ход урока:
Сегодня мы будем изучать с вами новый материал, но с начала повторим ранее изученный материал. Для этого нам нужно будет решить примеры.
(слайд )
Актуализация опорных знаний.
Устный счет
Записать только ответы:
1) -12-18
2) -20+10
3) Найти модуль -6
4) (-2)
5) Заменить неправильной дробью31/5
6) Заменить десятичной дробью 2/5
7) 5,2:1,3
8) - (а+в)
9) – (-а-в)
10) : 2
11) Заполнить схему (-)(-)=
(-)(+)=
(-)(-)=
12)Какие примеры мы пока еще не сможем решить? (на деление)
Дети поочерёдно выполняют устные примеры с рациональными числами:
1145. При каких значениях множителей произведение ху равно нулю? не равно нулю?
1146. В каких случаях может быть верно равенство: а) х = х 2; б) х = х3 ; в) х2 = х3?
1147. Проверьте на примерах справедливость равенства |аb| = |a| • |b|. Попробуйте доказать, что это равенство верно при любых значениях а и b.
1.2 Микрообобщение
2. Работа по теме урока: «Деление положительных и отрицательных чисел». (слайд 4)
Как же нам научиться делить отрицательные числа и числа с разными знаками
Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел: по данному произведению и одному из множителей находят второй множитель.
.1. Деление отрицательных чисел имеет тот же смысл, что и деление положительных чисел, т.е. по данному произведению и одному из множителей находят второй множитель.
Кто может назвать компоненты деления?
Например: -12 : (-4) =?
Что значит -12 : (-4) ? (Значит, найти такое число х, что при -4 • х = -12)
Теперь найдем знак числа х.
Как вы думаете, как это можно сделать?
Т.к. при умножении -4 на х получается отрицательное число -12 следовательно множители должны иметь разные знаки. Следовательно, х – положительное число.
Теперь найдем модуль числа х.
Как вы думаете, чему он будет равен?
Т.к. модуль произведения равен произведению модулей множителей, следовательно. Следовательно, т.к. х – положительное число, то х = следователь х = 3.(слайд 5)
Это записывается так:
или короче
(-12) : (-4) = 12: 4 = 3 (слайд 6)
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
Например, —4,5: ( — 1,5)=4,5:1,5 = 3;
Разделить — 12 на 4 — это значит найти такое число х, что 4 • х= —12. При умножении 4 на х получилось отрицательное число —12, значит, множители 4 и х должны иметь разные знаки. Поэтому х — отрицательное число. При этом должно выполняться равенство |4|•|x|=|—24|. Отсюда I х | = | — 12|:|4| =12:4 = 3. Значит, х — отрицательное число с модулем 3, т. е. х = — 3.
Итак, —12:4=—3.
Рассуждая таким же образом, получим, что 12:( —4)= —3.
При делении чисел с разными знаками, надо: 1) разделить модуль делимого на модуль делителя; 2) поставить перед полученным числом знак «—».
Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.
Например, 3,6:(— 3) = — (3,6:3) = —1,2;
При делении нуля на любое число, не равное нулю, получается нуль. Делить на нуль нельзя!
Сформулируйте правило деления отрицательного числа на отрицательное. Сформулируйте правило, деления чисел, имеющих разные знаки. Чему равно частное 0:а, где аО?
1133. Верно ли выполнено деление:
а) -36:2=-18; в) 2,7:(-1)=2,7;
б) 60:( —1,5)= —4; г) -7,5:(-5)=1,5?
1134. Найдите частное:
а) -38:19; д) — 6,1:(—17); и) 48,1 :(-48,1);
б) 45:( —15); е) 650:(-1,3); к) -950:9,5;
в) —36:( — 6); ж) -4,4:4; л) -5,42:(-27,1);
г) 270:( — 9); з) -8,6:( —4,3); м) 10,01:(-1,3).
Частное, в которое входят отрицательные числа, читают так:
-54:(— 2,7) — частное минус пятидесяти четырех и минус двух целых семи десятых — минус пятьдесят четыре разделить на минус две целых семь десятых (— 6m):( — 3) — частное минус шести эм и минус трех
— минус шесть эм разделить на минус три
Равенство, содержащее отрицательные числа, читают так:
минус две седьмых икс равны минус четырем одиннадцатым
1136. Выполните действия:
а) — 4•( — 6)—( — 30):6; д) (-8 + 32):(-6)-7;
б) 15:( —15)—( —24):8; е) -21+(-3-4 + 5):(-2);
в) -8(-3 + 12):36 + 2; ж) -6•4-64:(-3,3 + 1,7);
г) 2,3•(—6 —4):5; з) (-6+6,4-10):(-8)•(-3).
2
Правило: чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя. (ученики читают правило про себя, а затем рассказывают соседу по парте. Потом кто-то из учащихся рассказывает правило всему классу). (слайд 7)
2.2 Теперь разделим отрицательное число на положительное.
А теперь давайте проговорим алгоритм деления чисел с разными знаками, (учащиеся пытаются сами составить алгоритм). Итак:
1. разделить модуль делимого на модуль делителя;
2. поставить перед полученным числом знак минус. (слайд 10)
2.3 При делении нуля на любое число, не равное нулю, получается нуль.
И самое главное правило: Делить на нуль нельзя! (слайд 11) Вывод.
4)Заполнить схему: (-):(-)=
(+):(-)=
(-):(+)=
Чтобы разделить отрицательное число на отрицательное, надо разделить модуль делимого на модуль делителя.
При делении чисел с разными знаками, надо:
1) разделить модуль делимого на модуль делителя;
2) поставить перед полученным числом знак ?.
Делить на нуль нельзя!
5. Физкультминутка.
6. Закрепление нового материала:
3. Закрепление нового материала
3.1 № 1135 (три примера разбираются на доске, три с комментированием с места)
3.2 Самостоятельная работа № 1136 (все решают примеры, а затем 1 вариант проверяет у 2 варианта примеры с д - з, а 2 у 1 варианта проверяет примеры с а - г). На эту работу вам 8-10 минут.
а. -4 • (-5) – (-30) : 6 = 25
б. 15 : (-15) – (-24) : 8 = 2
в. -8 • (-3 + 12) : 36 + 2 = 0
г. 2,3 • (-6 – 4) : 5 = - 4,6
д. (-8 + 32) : (-6) – 7 = -11
е. -21 + (-3 - 4 + 5) : (-2) = - 20
ж. -6 • 4 – 64 : (-3,3 + 1,7) = - 64
з. (-6 + 6,4 – 10) : (-8) • (-3) = - 3,6 (примеры а, д слайд 14; б-г, е-з слайд 15; ответы слайд 16 )
решить № 1131, 1136 (устно), 1132 (1-7), 1134 (1-4), 1137(1).
Работа в парах:
1. -57+(-19)
2. 1,7-5,8
3.-5/8-7/12
4. -3+12/5
5. 55/14-(31/2-5/7)
6.-8,65*0
7.-5/9*(-12/25)
8.11/8*(-51/3)
9.48:(-16)
10. 4/9:(-8)
11. 5,25:(-1/20)
12. (-3)2*(-2)3
7. Самостоятельная работа.
Решить № 1137 (2). 1135 (6).
8. Итоги урока. Д/з. Рефлексия.
Решить на 7 баллов: № 1133(1-7), на 11 баллов: № 1138 (1, 2), 1135 (1-4).
Учащиеся по кругу высказываются одним предложением.
• Я научился…
• Было трудно…
• Сегодня я узнал…
• У меня получилось…
• Теперь я могу…
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Открытый урок " Умножение положительных и отрицательных чисел" »
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1670 руб.
2380 руб.
1970 руб.
2820 руб.
2000 руб.
2860 руб.
2000 руб.
2860 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства

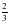 : 2
: 2