| 1.Организационный этап(1-2 мин) | Приветствие учителя, проверка подготовленности к учебному занятию, организация внимания учащихся. Учитель: «Ребята, Тема сегодняшнего урока «Определение синуса, косинуса и тангенса угла». | Включаются в деловой ритм урока. | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности Личностные: мотивация на обучение | фронтальная |
|
| 2.Объяснение нового материала.(3-5 мин) | Учитель:»Сегодня мы поднимемся на следующую ступеньку наших знаний «Тригонометрия». Вы узнаете определения синуса, косинуса, тангенса и котангенса угла, научитесь решать простейшие тригонометрические уравнения | Участвуют в работе: 1. в беседе с учителем отвечают на поставленные вопросы. | Познавательные: структурирование собственных знаний. Коммуникативные: организация и планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала. | 1. фронтальный опрос 2. Мини опрос 3.Работа в парах | 1.Устный опрос 3.Взаимопроверка (в парах) |
| 3.Изучение нового материала(7-10 мин) | Рассмотрим окружность радиуса, равного 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют Единичной или тригонометрической. 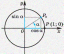
Рисунок 1 – точка Р на единичной окружности Точка Р (1; 0) при повороте вокруг начала координат на угол 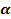 переместилась в точку Рₐ. Определим её координаты. (рис. 2). переместилась в точку Рₐ. Определим её координаты. (рис. 2). Определения. Синусом угла 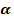 называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол называется ордината точки, полученной поворотом точки (1; 0) вокруг начала координат на угол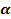 . . Обозначается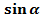 Косинусом угла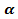 называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол называется абсцисса точки, полученной поворотом точки (1; 0) вокруг начала координат на угол 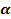 . . Обозначается  Угол 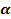 может выражаться и в градусах и в радианах может выражаться и в градусах и в радианах | Записывают дату в тетрадь, определяют тему, цель, задачи урока. | Познавательные: умение осознанно и произвольно строить речевое высказывание в устной форме. Личностные: самоопределение. Регулятивные: целеполагание. Коммуникативные: умение вступать в диалог, участвовать в коллективном обсуждении вопроса. | фронтальная | Устный опрос |
| 4.Закрепление нового материала Решение задач.(21-23 мин) | Пример 1. Точка А(1; 0) при повороте на угол 90 (рис. 1) (рис. 1) Ордината точки В равна 1, значит 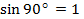 или или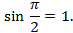 Абсцисса точки В равна 0, значит  Пример 2. Точка А(1; 0) при повороте на угол 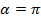 переместилась в точку переместилась в точку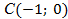 ( рис. 1) ( рис. 1) Найдите 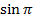 и и  Ответ: 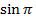 = 0; = 0; 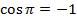 Пример 3. Точка А(1; 0) при повороте на угол 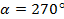 переместилась в точку переместилась в точку  (рис. 1) (рис. 1) Найдите 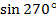 и и 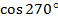 Ответ:  = =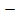 1 1 = 0 = 0 Рассмотрим ещё два понятия. Определение. Тангенсом угла 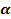 называется отношение синуса угла к его косинусу. называется отношение синуса угла к его косинусу. Обозначается tg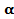 tg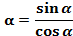 , ,  Пример 4. Найти tg 0. Вычислим по формуле tg  = = 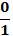 = 0. = 0. Определение. Котангенсом угла 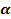 называется отношение косинуса угла к его синусу. называется отношение косинуса угла к его синусу. Обозначается сtg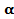 сtg Пример 5. Найти сtg  . . Вычислим по формуле сtg  = = 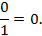 2. Меру угла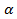 (в радианах) можно рассматривать как действительное число, поэтому (в радианах) можно рассматривать как действительное число, поэтому  и и 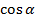 – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1; -1 ≤ у ≤ 1,то синус и косинус не могут превышать значения, больше – это числовые выражения. А так как каждая точка единичной окружности имеет координаты х и у такие, что выполняются неравенства -1 ≤ х ≤ 1; -1 ≤ у ≤ 1,то синус и косинус не могут превышать значения, больше 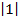 . . Чтобы решить уравнения  = а, = а,  нужно считать х неизвестным, число а – заданным. нужно считать х неизвестным, число а – заданным. Пример 6. Решить уравнение  = 1. = 1. Найдем точку с ординатой 1 и запишем, каким числам х она соответствует. На окружности мы видим эту точку: В (0; 1). Она соответствуют числу  и всем числам вида и всем числам вида 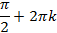 Решением уравнения 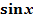 = 1 являются х = = 1 являются х =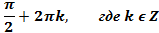 . . 3. Полезно знать синусы, косинусы, тангенсы некоторых углов. Для этого рассмотрим дугу единичной окружности в I четверти координатной плоскости (рис. 3). 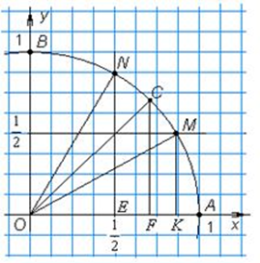
Рисунок 2 – 1 четверть единичной окружности Точки А (1; 0) и В (0; 1) нам знакомы. Рассмотрим ещё несколько точек на окружности и найдем их координаты. Точка С является серединой дуги АВ, значит угол АОС равен половине прямого угла, 45 или или  . Ордината точки С равна её абсциссе. Их значения нетрудно найти по теореме Пифагора из прямоугольного треугольника ОСF, оно равно . Ордината точки С равна её абсциссе. Их значения нетрудно найти по теореме Пифагора из прямоугольного треугольника ОСF, оно равно  А значит, А значит,   , ,
tg 45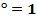 Дуга АМ составляет третью часть прямого угла,  . Ордината точки М равна . Ордината точки М равна  , значит , значит 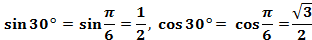 , tg30 , tg30 . .
Дуга АNсоставляет  прямого угла, прямого угла,  . Абсцисса точки N равна . Абсцисса точки N равна  , поэтому , поэтому 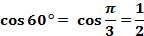 , , 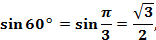 tg 60 tg 60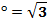 . .
Чтобы легче запомнить эти значения, придумали мнемоническое правило- правило на ладони (рис. 4). 
Рисунок 3 - мнемоническое правило- правило на ладони Расположим ладонь так, как на рисунке, пусть мизинцу соответствует угол 0 , следующим пальцам– 30 , следующим пальцам– 30 , 45, 60 , 45, 60 и 90 и 90 . Так же присвоим им номера: мизинец №0, следующие №1, №2, №3, №4. Чтобы найти синус, используем формулу: . Так же присвоим им номера: мизинец №0, следующие №1, №2, №3, №4. Чтобы найти синус, используем формулу: 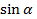 = =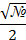 . А для косинуса нумерацию будем вести от большого пальца, выполняя вычисления по той же формуле. . А для косинуса нумерацию будем вести от большого пальца, выполняя вычисления по той же формуле.  = =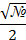 . . Например,  = = , ,  = =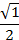 = = . . А тангенс можно вычислить по формуле: tg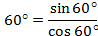 = = 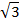 | Повторяют определения. Выполняют задания.
| Познавательные: формирование интереса к данной теме. Коммуникативные: Умение самостоятельно выполнять задание Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. | Групповая и и ндивидуальная работа | Устный опрос |
| 5.Рефлексия (подведение итогов урока) (2-3мин)
| Подводит итоги работы. 1.Организует работу по эмоциональной окраске 2. Организует работу по закреплению нового материала, запоминанию определений | Учащиеся анализируют свою работу, выражают вслух свои затруднения и обсуждают правильность решения задач. Оценивают свою работу. | Личностные: формирование позитивной самооценки Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли Регулятивные: Использование полученных знаний в нестандартных ситуациях, оценивание собственной деятельности на уроке | Индивидуальная работа |
|



















