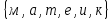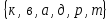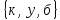Разработка урока, состоит из трех частей: начало средина и конец урока.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Методическая разработка урока "Проценты. Решение задач с помощью составления уравнения"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Методическая разработка урока "Проценты. Решение задач с помощью составления уравнения"»
Полезное для учителя
Распродажа видеоуроков!
1690 руб.
2820 руб.
1540 руб.
2560 руб.
1060 руб.
1760 руб.
1490 руб.
2480 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
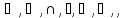 работая со множествами
работая со множествами

 ).
). 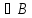 . Читают: «а-элемет множества В» или «а принадлежит множеству В».
. Читают: «а-элемет множества В» или «а принадлежит множеству В».  .(рис. 1 ).
.(рис. 1 ).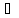 А Читают: с не принадлежит множеству А». Например, число 0 не принадлежит множеству натуральныхчисел N, записывают: 0
А Читают: с не принадлежит множеству А». Например, число 0 не принадлежит множеству натуральныхчисел N, записывают: 0 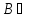 А
А 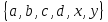 и D=
и D=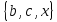
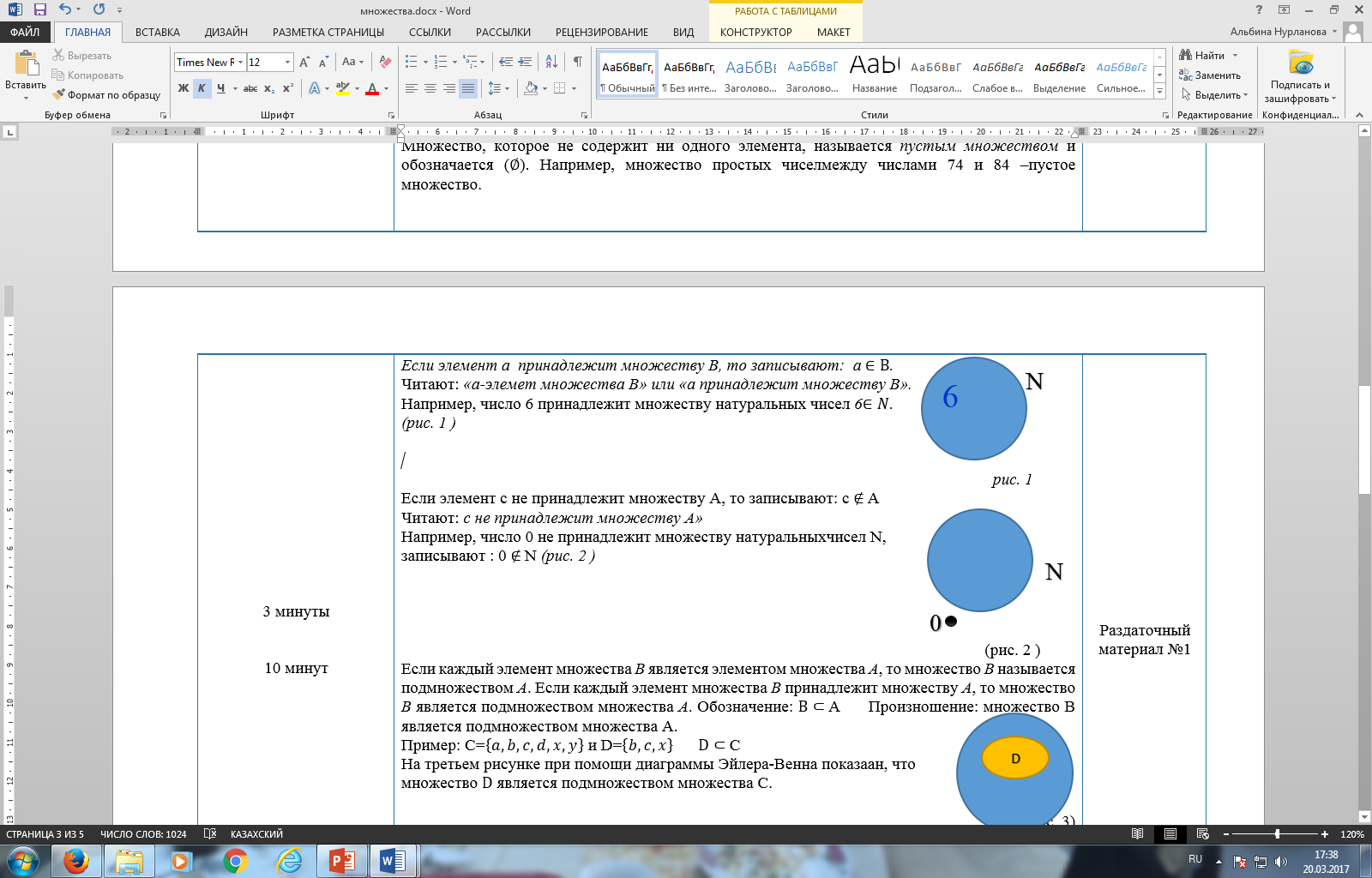
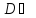 C. На третьем рисунке при помощи диаграммы Эйлера-Венна показаано, что множество
C. На третьем рисунке при помощи диаграммы Эйлера-Венна показаано, что множество 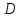 является подмножеством множества С.
является подмножеством множества С.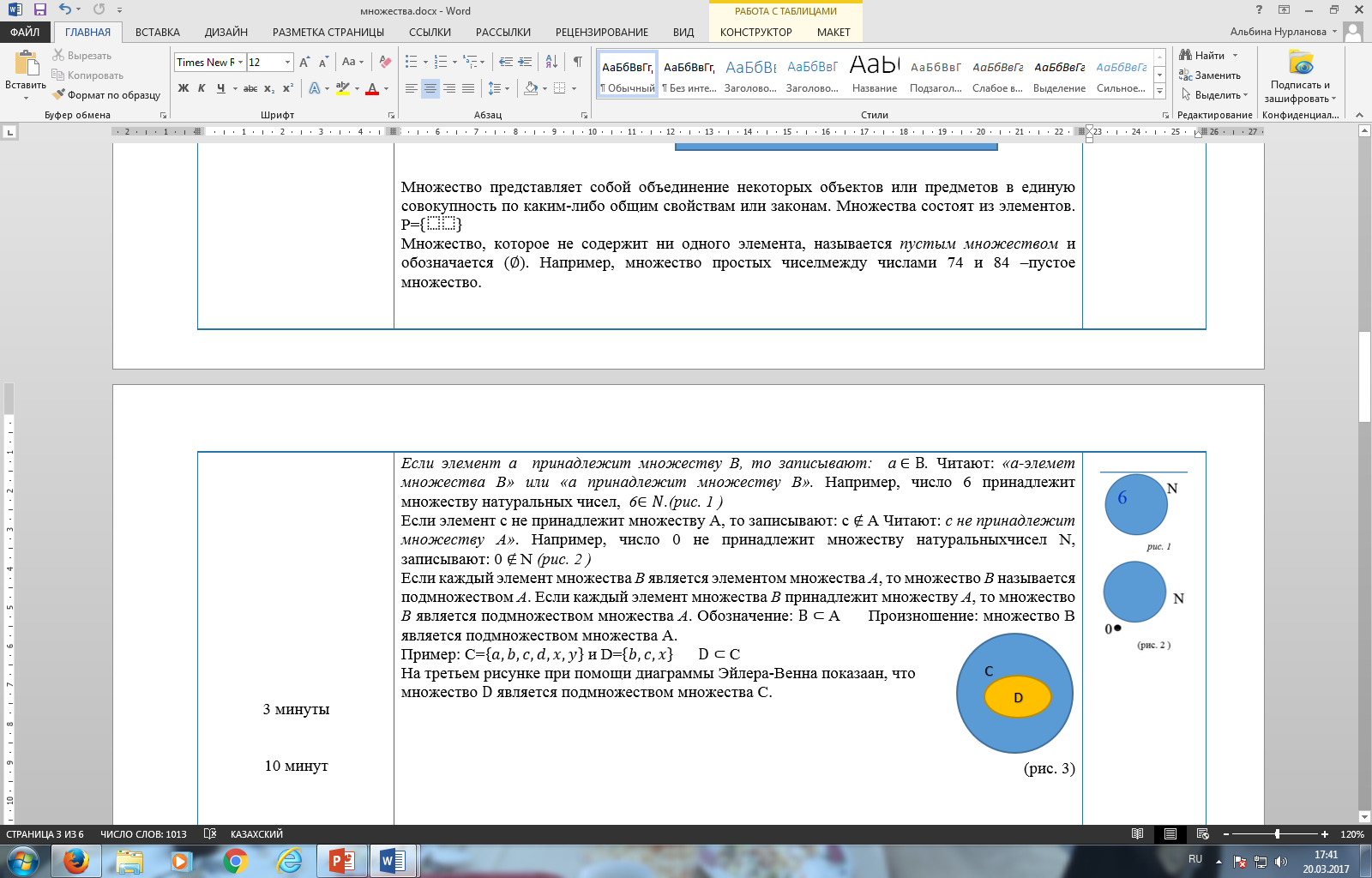
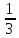 ; 60;
; 60; 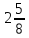 ; 0,4; 100 принадлежат и не принадлежат множеству N?
; 0,4; 100 принадлежат и не принадлежат множеству N? 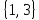 ; В=
; В= 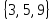 ; С=
; С=  ; және D=
; және D= 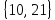 . Какое из них является подмножеством множества F=
. Какое из них является подмножеством множества F= 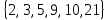 ? Сделайте соответствующие записи, используя знак «
? Сделайте соответствующие записи, используя знак «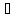 »
»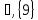 ; б)
; б) 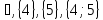 в)
в) 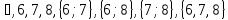 . Задайте множество К перечислением его элементов.
. Задайте множество К перечислением его элементов.