Государственное областное бюджетное
профессиональное образовательное учреждение
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»
Методическая разработка урока
математики
«Цилиндр. Решение задач».
Выполнил:
преподаватель математики
Заварзина В.Г.
Липецк 2016 г.
Тема урока: «Цилиндр. Площадь поверхности цилиндра».
Цели урока:
ввести понятие цилиндра; формирование понятия площади полной и боковой поверхности цилиндра; вывести формулы площади поверхности цилиндра и сформировать умения применять их при решении задач; проверить уровень первичного усвоения материала учащегося;
развитие пространственного мышления, культур математической речи; развитие коммуникативных умений: умение слушать и слышать, правильно задавать вопросы;
воспитание ответственного отношения к учебному труду.
Тип урока: введение нового материала
Методические приемы:
-практический- решение задач
Межпредметные связи: черчение, история
Оборудование и наглядные средства обучения: мультимедийный проектор, интерактивная доска, презентация, учебник “Геометрия 10-11 классы” авторы: Л. С. Атанасян, В. Ф. Бутузов
Методическая цель: активизировать мыслительную деятельность обучающихся.
Ход урока.
I. Организационный момент
Приветствие преподавателем студентов.
Преподаватель;
- Сегодня весь урок мы посвятим обобщению знаний о цилиндре.
В ходе фронтального опроса студентам предлагается ответить на следующие вопросы:
Назовите знакомые вам фигуры вращения (круг, окружность)
Что лежит в основании цилиндра? (круг)
Дан отрезок АВ. Какая фигура получится при вращении вокруг точки А, точки В? (окружность)
5. Какую фигуру образует отрезок АВ при вращении его вокруг точки А? (круг с центром в точке А и радиусом, равным отрезку АВ)
6. Дайте определение цилиндра.
Ответ:
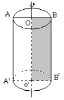 Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
7. Как можно получить эту фигуру?
Ответ:
Цилиндр получается при вращении прямоугольника вокруг стороны.
8. Назовите элементы данного цилиндра (рисунок выше).
Ответ:
прямая OO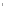 - ось цилиндра
- ось цилиндра
отрезок OO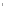 - высота,
- высота,
отрезок АА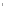 = ВВ
= ВВ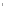 - образующая
- образующая
круг (О,ОВ) =кругу (O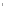 , O
, O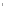 В
В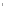 ) – основание цилиндра
) – основание цилиндра
9. Что называется касательной плоскостью к цилиндру?
Ответ:
Касательной плоскостью к цилиндру называется плоскость проходящая
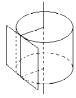 через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
10. По какой формуле находится площадь круга?
Ответ:
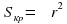
11. Что называется высотой цилиндра?.
Ответ:
Длина образующей называется высотой цилиндра.
(Пока ребята будут отвечать на вопросы, другие студенты получают карточки. Преподаватель раздает листочки с заданиями, студенты заполняют и сверяют свои ответы с правильными, названными учителем)
Пример карточки
1. Нанесите на рисунок основные элементы цилиндра.
2. Изобразите а) осевое сечение цилиндра; б) сечение цилиндра плоскостью, проходящей перпендикулярно оси цилиндра; в) сечение цилиндра плоскостью, проходящей параллельно оси цилиндра. Какая фигура получается в каждом случае?
III. Актуализация знаний.
(заранее подготовленная студентом)
Историческая справка
Слово цилиндр происходит от греческого слова , что означает “валик”, “каток”. Конус в переводе с греческого “konos” означает “сосновая шишка”. С конусом и цилиндром люди знакомы с глубокой древности. В 1906 году была обнаружена книга Архимеда (287–212 гг. до н. э. ) “О методе”, в которой дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед приписывает честь открытия этого принципа – Демокриту (470–380 гг. до н. э. ) – древнегреческому философу - материалисту. С помощью этого принципа Демокрит получил формулу для вычисления объема пирамиды и конуса.
Много сделала для геометрии школа Платона (428–348 гг. до н. э. ). Платон был учеником Сократа (470–399 гг. до н. э. ). Он в 387 г. до н. э. основал в Африке Академию, в которой работал 20 лет. Каждый, входящий в Академию, читал надпись: “Пусть сюда не входит никто, не знающий геометрии”. Школе Платона с частности принадлежит: а) исследование свойств призмы, пирамиды, цилиндра и конуса; б) изучение конических сечений.
Большой трактат о конических сечениях был написан Аполлонием Пергским (260–170 гг. до н. э. ) – учеником Евклида (III в. до н. э. ), который создал великий труд из 15 книг под названием “Начала”. Эти книги издаются и по сей день, а в школах Англии по ним учатся до сих пор.
Цили́ндр (др. - греч. κύλινδρος — валик, каток) — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью, называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями - это основания цилиндра. Таким образом, граница основания будет по форме совпадать с направляющей. Цилиндр - это тело полученное в результате вращения прямоугольника, относительно одной из его сторон.
В большинстве случаев под цилиндром подразумевается прямой круговой цилиндр, у которого направляющая — окружность и основания перпендикулярны образующей. У такого цилиндра имеется ось симметрии.
Другие виды цилиндра — (по наклону образующей) косой или наклонный (если образующая касается основания не под прямым углом); (по форме основания) эллиптический, гиперболический, параболический.
Призма также является разновидностью цилиндра — с основанием в виде многоугольника.
Преподаватель: Ребята, возникла проблема, моему знакомому мальчику для выступления на сцене необходимо изготовить из бумаги шляпу в виде кругового цилиндра. Как ему помочь?
(Студенты предлагают свои идеи решения проблемы).
Необходимо измерить охват головы (это длина окружности основания цилиндра).
Пусть L =30 см.
Вычислить радиус окружности по формуле: L =  R.
R.
R = L/ .
.
R = 30/ ~ 4,7 см ~ 5 см
~ 4,7 см ~ 5 см
Развёртка цилиндра это прямоугольник, являющийся боковой поверхностью цилиндра и два круга, являющиеся основаниями цилиндра. Нам необходимо построить прямоугольник и один круг.
Стороны прямоугольника это длина окружности (L = 30 см) и произвольная высота (высота цилиндра). Пусть высота Н = 20 см.
Определим сколько бумаги нам необходимо. Для этого вычислим площадь прямоугольника и площадь круга. Затем их сложим.
Sпр. = L *Н = 30*20 = 600см2; Sкр =  R 2 = 3.14*52 ~ 79см2 . Площадь необходимой бумаги: 600+79 = 679 см2. Разделим на высоту цилиндра. Получим длину рулона бумаги шириной 20 см. 679/20 = 33,95 см. Итак рулон бумаги 33,95см на 20 см.
R 2 = 3.14*52 ~ 79см2 . Площадь необходимой бумаги: 600+79 = 679 см2. Разделим на высоту цилиндра. Получим длину рулона бумаги шириной 20 см. 679/20 = 33,95 см. Итак рулон бумаги 33,95см на 20 см.
Осталось вырезать прямоугольник со сторонами 20см на 30 см и круг радиусом 8 см(учесть напуски для склеивания бумаги).
Преподаватель: Попробуйте записать формулу которая получается в результате нахождения объёма необходимой бумаги, но теперь учтите оба основания цилиндра. (Обучающиеся работают самостоятельно).
Приходят к выводу: S =  RН + 2
RН + 2 R 2= 2
R 2= 2 R(Н+ R).
R(Н+ R).
Преподаватель: Сформулируйте на математическом языке, что вычисляют по данной формуле.
Ответ: Площадь поверхности цилиндра.
Преподаватель: Вы сами вывели формулу для вычисления площади поверхности цилиндра. Запишите эту формулу в тетрадь. Sп.п.ц. =  RН + 2
RН + 2 R 2= 2
R 2= 2 R(Н+ R).
R(Н+ R).
VI. Решение задач.
 Задачи для устного решения.
Задачи для устного решения.
Задача №1.
Дано: d = 8 м
Найти: Sкруга
Sкруга = πR2
Ответ: 8π м2
Задача №2.
Дано: ОА= 8,
Найти: l
l=2πR
Ответ:16π
Задача №3.
Дано: ABCD –прямоугольник,
CD=3, AC=5

 Найти: SABCD
Найти: SABCD
Ответ: 12
А
Преподаватель: Как вычислить площадь боковой поверхности цилиндра?
Ответ: Sб.п.ц. =  RН
RН
Преподаватель:
-Давайте решим следующие задачи на доске.
Задача 1.
Радиус основания цилиндра равен 17, высота равна 5. Найдите площадь боковой поверхности цилиндра, деленную на π.
Решение:
Площадь боковой поверхности цилиндра вычисляется по формуле 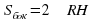 , где H– высота цилиндра, R– радиус.
, где H– высота цилиндра, R– радиус.
Тогда 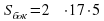 =150π
=150π
Следовательно, 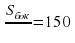
Ответ: 150.
Задача 2.
Площадь осевого сечения цилиндра равна 23. Найдите площадь боковой поверхности цилиндра, деленную на π.
. 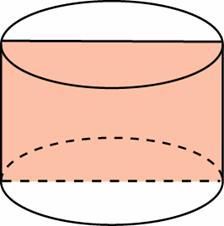
Решение:
Площадь осевого сечения цилиндра есть 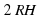 (где H– высота цилиндра, R– радиус). Поэтому
(где H– высота цилиндра, R– радиус). Поэтому
23= 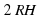
Площадь боковой поверхности цилиндра равна 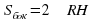 ,
,
Подставляя в последнюю формулу значение , получаем
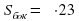
Тогда 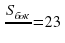
Ответ: 23.
V. Самостоятельная работа.
Раздаточный материал: карточки (для тестовой работы по 2-м вариантам)
Вариант - 1
1. Радиус основания цилиндра равен 2 см, высота – 5 см, тогда площадь боковой поверхности равна:
| А) 10π см2 | В) 20π см2 | С) 4π см2 | D) 20π см | E) 40π см2 |
2. Радиус основания цилиндра в два раза меньше образующей, равной 4а, тогда площадь боковой поверхности равна:
| А) 8а2π | В) 24а2π | С) 4а2π | D) 48а2π | E) 16а2π |
Вариант - 2
1. Радиус основания цилиндра равен 8 см, высота – 3 см, тогда площадь полной поверхности равна:
| А) 66π см2 | В) 112π см2 | С) 80π см2 | D) 128π см2 | E) 176π см2 |
2. Радиус основания цилиндра в два раза больше образующей, равной 3m, тогда площадь боковой поверхности равна:
| А) 12m2π | В) 108m2π | С) 36m2π | D) 9m2π | E) 6m2π |
Бланки ответов (ключ к тесту):
| Вариант - 1
| В Е А |
| Вариант - 2
| Е С Д |
Для слабых ребят предлагается следующий тест.
Тест по теме: «Площадь поверхности цилиндра»
1. По какой формуле можно вычислить длину окружности?
а)S =  RН б)S = 2
RН б)S = 2 R(Н+ R) в) L =
R(Н+ R) в) L =  R г)L =
R г)L =  RН д)S =
RН д)S =  R 2
R 2
2. По какой формуле можно вычислить площадь круга?
а)S =  RН б)S = 2
RН б)S = 2 R(Н+ R) в) L =
R(Н+ R) в) L =  R г)L =
R г)L =  RН д)S =
RН д)S =  R 2
R 2
3. Цилиндр это
а)многогранник б)тело вращения в)фигура планиметрии
4.Вычислить площадь круга, если радиус равен 3 м
а)9 м2 б)6
м2 б)6 м2 в)3
м2 в)3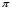 м2 г) не достаточно условий
м2 г) не достаточно условий
5.Что обозначают буквой Н в формулах?
а)высоту б)образующую в)радиус г)диаметр
6.Что является осевым сечением цилиндра?
а)круг б)треугольник в)квадрат г)прямоугольник
7.Какая фигура является развёрткой боковой поверхности цилиндра?
а)круг б)квадрат в)прямоугольник г) прямоугольник и круг
8.Чему равен угол прямого цилиндра между основанием и образующей?
а)180° б) 90° в)45° г)0° д)60°
9.Сколько образующих у цилиндра?
а)одна б) две в)много г) четыре
10.Боковая поверхность цилиндра содержит основание?
а) да б) нет
Дается время на выполнение работы на листочках. Листочки сдаются преподавателю.
IV. Рефлексия.
Что мы сегодня нового узнали на уроке?
С каким новым телом познакомились?
Как найти площадь полной поверхности цилиндра?
Итог урока: озвучивание и комментирование оценок.
Домашнее задание:
§1п.60 № 522,523 из учебника.
Спасибо за урок!
Список литературы:
1. Г. Глейзер. История математики в школе. 9-10 классы. Пособие для
учителя. «Теорема Эйлера» о многогранниках. О правильных многогранниках. 1983 г.
2. Детская энциклопедия. Том № 2, 1965 г. Леонард Эйлер. 3. Энциклопедия для детей. Том № 11, 1998 год. Многогранники.
3. М. Веннинджер. Модели многогранников. Перевод с английского.
1974 г.
4. А. Погорелов. Геометрия. 10-11 класс. 2004 г.
5. Ю. Киселев. Геометрия. 11 класс. 2008 г. Историческая справка.
6. Геометрия 10-11 классы Л. С. Атанасян, В. Ф. Бутузов. 2012г.
 Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.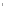 - ось цилиндра
- ось цилиндра через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
через образующую цилиндра и перпендикулярная плоскости осевого сечения, содержащей эту образующую.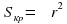


 Задачи для устного решения.
Задачи для устного решения.
 Найти:
Найти: 
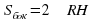 , где
, где 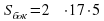 =150
=150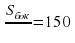

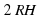 (где
(где 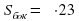
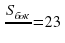
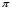 м2 г) не достаточно условий
м2 г) не достаточно условий






















