Содержание.
Пояснительная записка………………………………………………..............2
Функция у = kx + b и ее график………………………………………………3
Урок №1……………………………………………………………………….3
Урок №2……………………………………………………………………….5
Линейная функция и ее график………………………………………………7
Урок №3…….…………………………………………………………………7
Урок №4……………………………………………………………………….9
Урок №5 «Своя игра» (урок обобщения и повторения)…………………..11
Список литературы………………………………………………………….15
Пояснительная записка.
Методическая разработка представляет собой серию уроков по теме «Линейная функция и ее график» к учебнику алгебры для 8 класса (авторы С.М. Никольский, М. К. Потапов, Н.Н. Решетников, А.В. Шевкин – М.: Просвещение, 2009) с мультимедийным приложением (CD) к каждому уроку в виде презентаций, содержащих как информативные материалы, так и задания для закрепления и контроля усвоения изученного материала.
Разработка материала по данной теме обусловлена тем, что задания по этой теме включены в материалы Государственной итоговой аттестации за курс основной школы, а также в КИМы промежуточных мониторингов. Однако практика показывает, что задачи с графиками функций вызывают затруднения у учащихся, и очень многие не имеют прочных навыков по данной теме.
Предлагаемая разработка наглядно демонстрирует учащимся взаимное расположение графиков функций. Познавательный материал способствует не только выработке умений и навыков, но и формированию устойчивого интереса к процессу и содержанию деятельности, а также познавательной активности.
Цели разработки:
ввести понятия прямой пропорциональной зависимости и линейной функции, выработать умение решать задачи, связанные с графиками данных функций;
развивать математические способности учащихся, продолжить формирование умений логически мыслить и отыскивать закономерности;
создавать положительную мотивацию, активизировать познавательную деятельность.
Задачи разработки:
обучить навыкам построения графиков и проведению преобразований графиков с помощью изученных методов;
научить распознавать графики;
развивать общеучебные умения и навыки;
развивать умение систематизировать получаемые знания.
Данная разработка предполагает компактное и четкое изложение теоретического материала, задания для устной работы, решение типовых задач, самостоятельную работу, также приведены критерии оценивания самостоятельных работ при само-, или взаимопроверки, задачи для домашнего решения. В разработке приводится примерное распределение учебного времени, план занятий.
Основные формы организации учебных занятий: объяснение материала в форме беседы, выполнение тренировочных задач, фронтальная и самостоятельная работа, работа в группах.
Все занятия направлены на развитие познавательного интереса учащихся к предмету, на расширение представлений об изучаемом материале, дают возможность подготовиться к успешному решению заданий по данной теме на ГИА.
Урок 1.
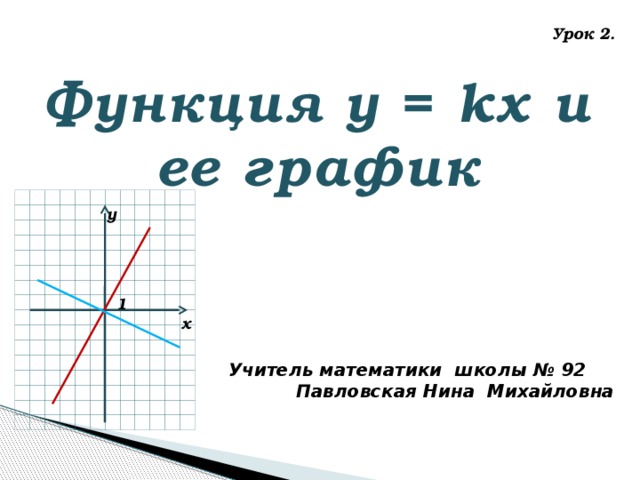
Тема урока: Функция у = kx и ее график.
Тип урока: урок изучения нового материала.
Цели урока:
систематизировать и развивать у учащихся знания по теме функция, область определения функции, график функции;
ввести понятие прямой пропорциональности;
сформировать умение строить и читать график функции, заданной формулой у = кх;
научиться определять:
- положение графика на координатной плоскости,
- принадлежность данной точки графику;
научиться по графику задавать формулой прямую пропорциональность;
способствовать развитию познавательного интереса учащихся
побуждать учеников к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
Оборудование: Экран, компьютер, мультимедийный проектор.
Ход урока
Мотивация учебной деятельности учащихся, постановка целей и задач урока (1–2 мин)
(слайд 2)
Актуализация знаний.
Устная работа (2–3 мин)
(слайд 3)
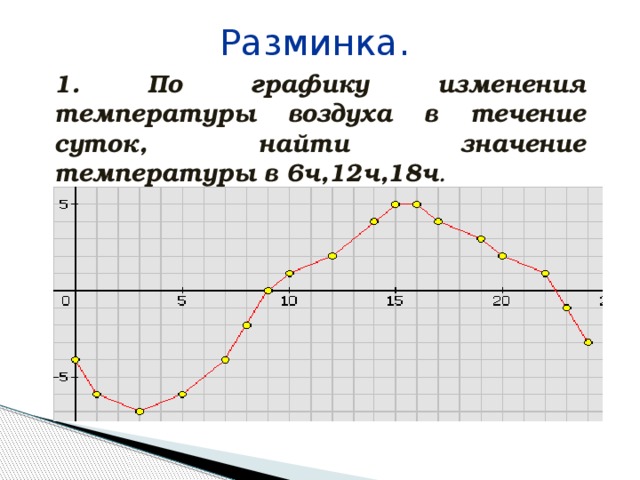
По графику изменения температуры воздуха в течение суток (рис. 1), найти значение температуры в 6ч,12ч,18ч.
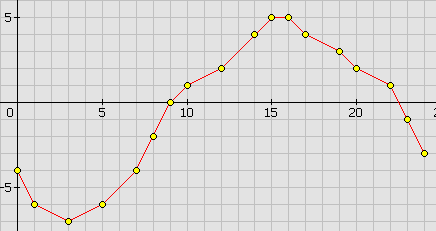 рис. 1
рис. 1
Что называют функцией, графиком функции?
Что называют областью допустимых значений переменной алгебраической дроби?
Найдите допустимые значения переменной для дроби: (слайд 4)
а) 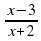 (х ≠ – 2); б)
(х ≠ – 2); б) 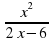 (х ≠ 3); в)
(х ≠ 3); в) 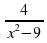 (х ≠ ±3); г)
(х ≠ ±3); г) 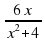 (х
(х R).
R).
Изучение нового материала (8–9 мин)
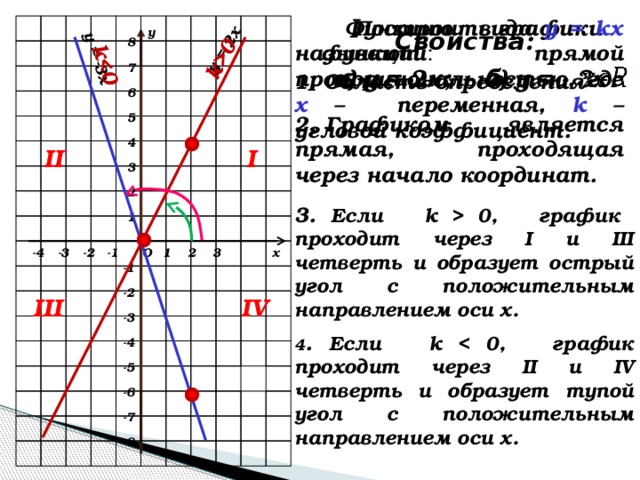
Построить в одной системе координат графики функций у = 2х и у = – 3х.
Ввести понятие прямой пропорциональной зависимости.
(слайд 5)
Функцию вида у = кх, где k ≠ 0 называют прямой пропорциональной зависимостью (прямой пропорциональностью).
k – коэффициент пропорциональности или угловой коэффициент прямой у = kх.
Свойства:
Область определения функции: х  R
R
Графиком является прямая, проходящая через начало координат.
При k0 – график проходит через I и III четверть, образует острый угол с положительным направлением оси х.
При k0 – график проходит через II и IV четверть, образует тупой угол с положительным направлением оси х.
В одной системе координат построить графики функций:
у = 5х; у = – 3х; у = 0,2х; у = – 0,5х.
Найти особенности их расположения и сделать вывод. (слайд 6)
При |k| 1 график вытягивается вдоль оси ординат.
При |k| график вытягивается вдоль оси абсцисс.
Закрепление изученного материала (20–25 мин)
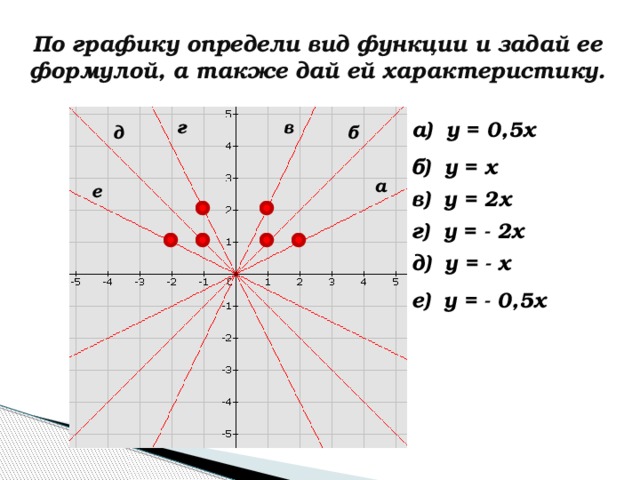
Определить, какой формулой задан каждый из графиков, изображенных на рис. 2.
(слайд 7)

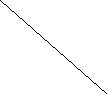


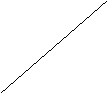

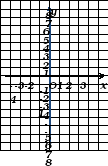 рис. 2
рис. 2 Ответы:
Так как у = kх
а) у = 0,5х
б) у = х
в) у = 2х
г) у = - 2х
д) у = - х
е) у = - 0,5х
е
дд
г
в
б
а
Решить устно: № 490, 491.
Письменно: № 493, 494(а, в), 495(а, в)
Ответить на вопросы. (слайд 8)
Что является графиком функции у = кх?
Что называют угловым коэффициентом прямой у = кх?
В каких координатных четвертях расположен график функции у = кх при k0, при k0?
Итоги урока (1–2 мин)
Домашнее задание (1–2 мин)
(слайд 8)
п.6.1, 6.2 учебника, № 494(б, г), 495(б, г), 496.
№ 644 – по желанию.
Урок 2.
Тема урока: Функция у = kx и ее график.
Тип урока: комбинированный урок.
Цели урока:
систематизировать и развивать у учащихся знания по теме функция, область определения функции, график функции;
провести контроль приобретенных знаний;
развивать логическое мышление, умение анализировать, делать вывод;
Оборудование: Экран, компьютер, мультимедийный проектор, карточки для самостоятельной работы.
Ход урока
Мотивация учебной деятельности учащихся, постановка целей и задач урока (1–2 мин) (слайд 2)
Актуализация знаний.
Устная работа. (3–4 мин) (слайд 3)
Какие из формул задают прямую пропорциональность?
а) у = –3х; б) у = 0,5х; в) у = –х; г) у = х2; д) у =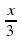 ; е) у = 2 – х;
; е) у = 2 – х;
ж) у = 5х – 1; з) у = 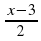 ; и) у = х.
; и) у = х.
(слайд 4)
В каких координатных четвертях расположены графики функций? а) у = 200х; б) у = – 0,201х; в) у = 2010х.
Принадлежат ли точки А(38;–15) и В(– 13;–3,9) графику функции у = 0,3х.
При каком k точки А(1;2), В(– 2;8); С(1;0,5) принадлежат графику функции у =kх.
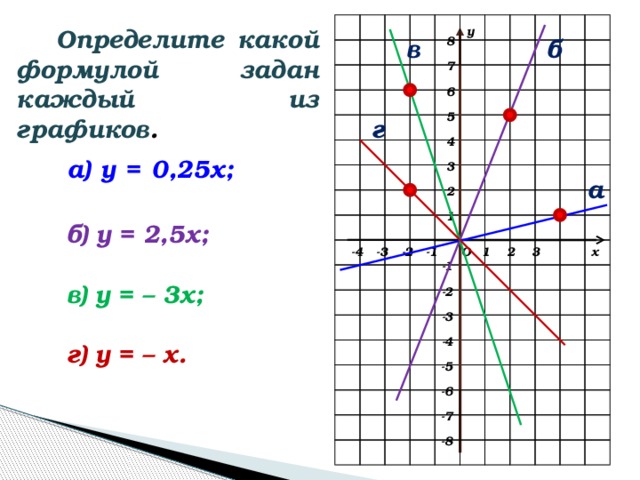
Определите, какой формулой задан каждый из графиков на рис. 3. (слайд 5)
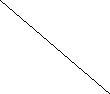

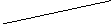

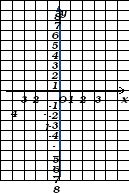 рис.3
рис.3 Ответы:
а) у = 0,25х;
б) у = 2,5х;
в) у = – 3х;
г) у = – х.
г
б
а
в
Проверка домашнего задания. (2–3 мин)
Формирование умений и навыков (15 мин)
№ 498 (Исследовать функцию у = 3х по плану.)
№ 501 (а, б); №503(а, б, в); №506(а, в, д)
Самостоятельная работа (10 мин) (слайд 6)
Вариант 2.
В каких координатных четвертях расположен график функции:
а) у = – 5 х; б) у = 0,4х.
Задайте формулой график прямой, проходящей через точку В( – 1; 2,3).
Постройте в одной системе координат графики функций:
а) у = 2,5х; б) у = – х ; в) у = –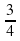 х
х
Вариант 1.
В каких координатных четвертях расположен график функции:
а) у = 4х; б) у = – 0,7х.
Задайте формулой график прямой, проходящей через точку А(3; – 1,5).
Постройте в одной системе координат графики функций:
а) у = 1,5х; б) у = х; в) у = – 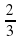 х
х
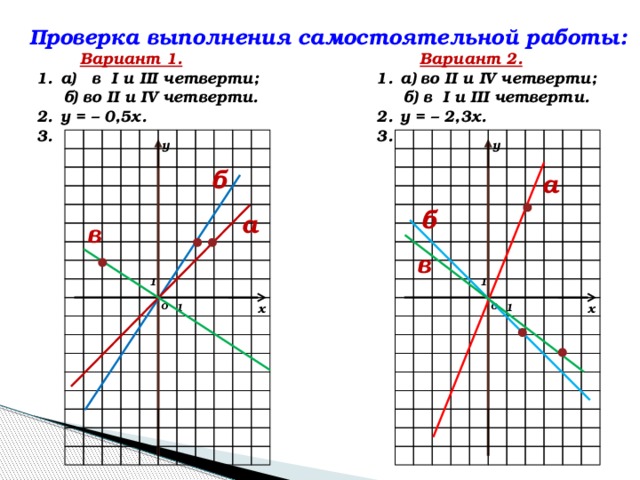
После выполнения работы проверка решения (2–3 мин) (слайд 7)
Критерии оценивания (слайд 8)
Верно выполнены задания 1 и 2 – «3»
Верно выполнены задания 1, 2 и 3(а) или 3(а,б) – «4»
Верно выполнены задания 1,2 и 3 – «5»
Подведение итогов, выставление оценок (1-2 мин)
Домашнее задание (1-2 мин) (слайд 9)
П. 6.1, 6.2 учебника, №499, №503(г, д, е), №506(г, е). № 510 – по желанию.
Урок 3.
Тема урока: Линейная функция и ее график.
Тип урока: урок изучения нового материала.
Цели урока:
ввести понятие «линейной функции»;
сформировать умение строить и читать график функции, заданной формулой у = кх+в;
научиться определять:
- положение графика на координатной плоскости,
- взаимное расположение графиков двух линейных функций,
- принадлежность данной точки графику;
научиться задавать формулой линейную функцию, график которой параллелен данной прямой или пересекает ее;
способствовать развитию наблюдательности, умению анализировать, сравнивать и делать выводы;
побуждать учеников к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
Оборудование: Экран, компьютер, мультимедийный проектор.
Сообщить тему урока, цели урока (1-2 мин) (слайд 2)
Устная работа(5 мин) (слайд 3)
1) Опрос по теории:
Что называют функциональной зависимостью?
(зависимость одной переменной от другой)
Как называется независимая переменная? (аргумент)
Как называют зависимую переменную? (функция)
Что называют областью определения функции?
(множество допустимых значений аргумента, при которых функция имеет смысл)
(слайд 4)
2) Найдите область определения функции
а) у = 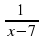 (х ≠ 7);
(х ≠ 7);
б) у = 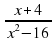 (х ≠ ±4); в) у = х2+ 8 (х
(х ≠ ±4); в) у = х2+ 8 (х R).
R).
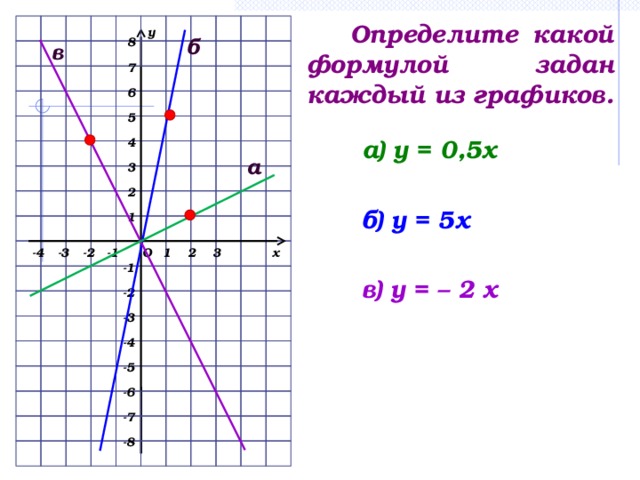
3) Определите какой формулой задан каждый из графиков на рис. 4.
(слайд 5)



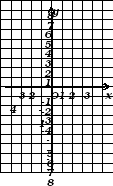 рис. 4
рис. 4 Ответы:
а) у = 0,5х;
б) у = 5х;
в) у = -2х.
в
б
а
Проверка домашнего задания фронтально (1-2 мин)
Изучение нового материала (7-10 мин)
Решить задачи. (слайд 6):
Стоимость одного бланка телеграммы 10 руб., а одного слова 5 руб. Какова зависимость стоимости телеграммы (с) от количества слов (т)?
с = 5т + 10
Тело, начальная скорость которого 15 м/с движется с постоянным ускорением 0,6м/с. Чему равна зависимость скорости (v) от времени (t)?
v = 0,6t + 15
Вывод 1:
Функцию вида у = kх + b, где k и b заданные числа называют линейной функцией.
Областью определения функции у = kх + b является множество всех действитльных чисел R.
Графиком функции у = kх + b является множество точек координатной плоскости хОу с координатами (х; kх + b), где х любое действительное число. Для построения графика достаточно двух точек.
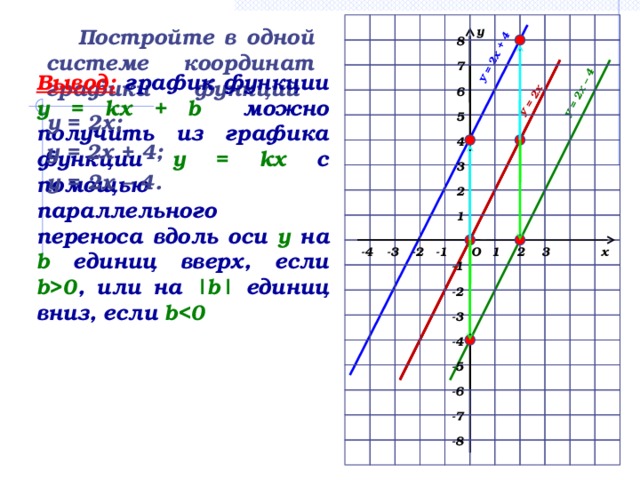
Практическе задание. (слайд 7)
Построить в одной системе координат графики функций: у = 2х; у = 2х + 4; у = 2х – 4, сделать соответствующие выводы.
Вывод 2:
График функции у = kх + b, можно получить из графика функции у = kх с помощью параллельного переноса вдоль оси у на b единиц вверх, если b 0, или на |b| единиц вниз, если b .
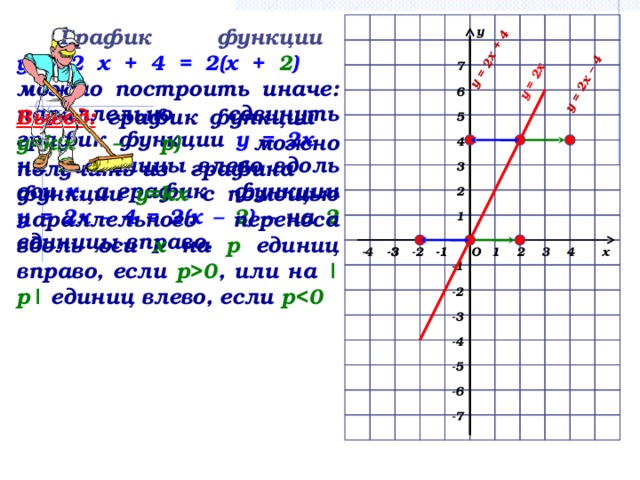
Вывод 3: (слайд 8)
График функции у = k(х – p), можно получить из графика функции у = kх с помощью параллельного переноса вдоль оси х на р единиц вправо, если р 0, или на |р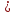 единиц влево, если р
единиц влево, если р 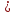 0.
0.
Это важно знать: (слайд 9)
Коэффициент k в уравнении у = kх + b называют угловым коэффициентом этой прямой.
Число b есть ордината точки пересечения прямой у = kх + b с осью ординат.
Прямые у = kх + b и у = k1х + b1 параллельны, если k = k1, а b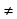 b1.
b1.
Прямые у = kх + b и у = k1х + b1 пересекаются, если k 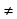 k1.
k1.
Если k = 0, то графиком функции у = b является прямая параллельная оси абсцисс и пересекающая ось ординат в точке (0; b)
Закрепление (20 мин).
Устная работа: (слайд 10)
Определите точки пересечения графиков функций с осью ординат.
а) у = 2х + 5 (0;5) б) у = -0,5х – 1,5 (0; - 1,5)
в) у = -х –7 (0;7) в) у = 7,5 (0;7,5)
В каких координатных четвертях расположены графики функций.
а) у = 0,5х + 3 (1,2,3) б) у = 3х – 2 (1,3,4)
в) у = -х – 0,5 (2,3,4) в) у = -2х + 7 (1,2,4)
Практические задания: (слайд11)
Фронтальная работа.
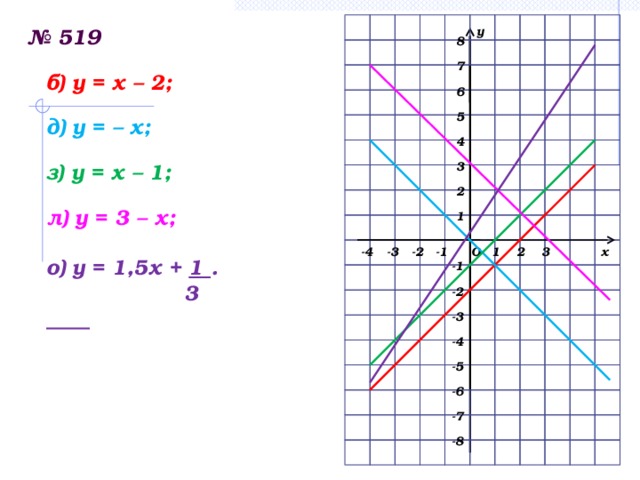
№ 516; №519(а,г,ж,к); №517, 530 – устно
Итоги урока (1-2 мин).
Домашнее задание: (1-2 мин) (слайд 11)
п. 6.3 учебника, №515; №519(б,д,з,л,о), № 531, 646 – по желанию.
Урок 4.
Тема урока: Линейная функция и ее график.
Тип урока: комбинированный урок.
Цели урока:
способствовать развитию наблюдательности, умению анализировать, сравнивать и делать выводы, развивать логическое мышление;
провести контроль приобретенных знаний;
побуждать учеников к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.
Оборудование: Экран, компьютер, мультимедийный проектор, презентация «Линейная функция и ее график», карточки для самостоятельной работы.
Сообщить тему урока, цели урока (1 – 2 мин) (слайд 2)
Актуализация опорных знаний (3 - 5 мин)
На экран проецируются задания для устной работы (слайд 3)
Фронтальная работа.
Какую функцию называют линейной?
Что называют угловым коэффициентом линейной функции?
При каком условии 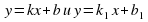 параллельны?
параллельны?
Какие из следующих функций являются линейными? Назовите k и b в линейных функциях.
а) у = 5х – 1; б) у = 2х2 + 3; в) у = 0,5 – х; г) у = 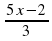 ; д) у =
; д) у = 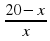 .
.
Какие из функций имеют параллельные графики:
а) у = 2х – 3; б) у = 2 + х; в) у = 4х – 3; г) у = 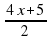 ; д) у = 2х2 + 1; е) у = 2х.
; д) у = 2х2 + 1; е) у = 2х.
Проверка домашнего задания (2 – 3 мин) (слайд 4 – 5)
Проверка домашнего задания осуществляется с помощью презентации, ребята обмениваются тетрадями.
Закрепление изученного материала (15 мин) (слайд 6)
Фронтальная работа.
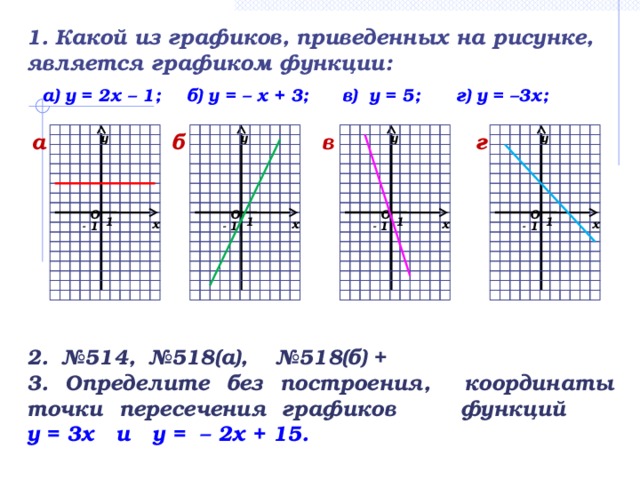
Какой из графиков, приведенных на рисунке, является графиком функции:
а) у = 2х – 1; б) у = – х + 3; в) у = 5; г) у = – 3х;
а) б) в) г)




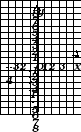
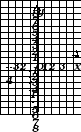
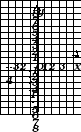
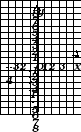
Исследовать функцию у = – 2х + 1 по плану (№514 учебника).
№518(а) 1 ученик у доски (Какой формулой задана прямая, проходящая через точки (0;8) и (1;12)); №518(б) – самостоятельно, с последующей проверкой.
Определите без построения, координаты точки пересечения графиков функций у = 3х и у = – 2х + 15.
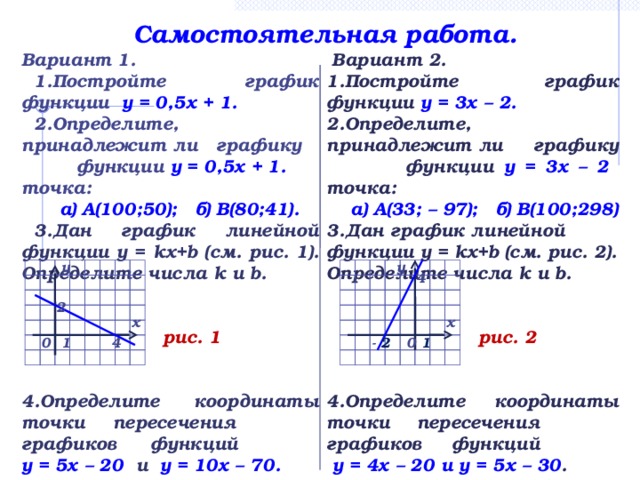
Самостоятельная работа. (10 мин) (слайд 7)
Вариант 2.
Постройте график функции у = 3х – 2.
Определите, принадлежит ли графику функции у = 3х – 2 точка:
а) А(33; – 97); б) В(100;300)
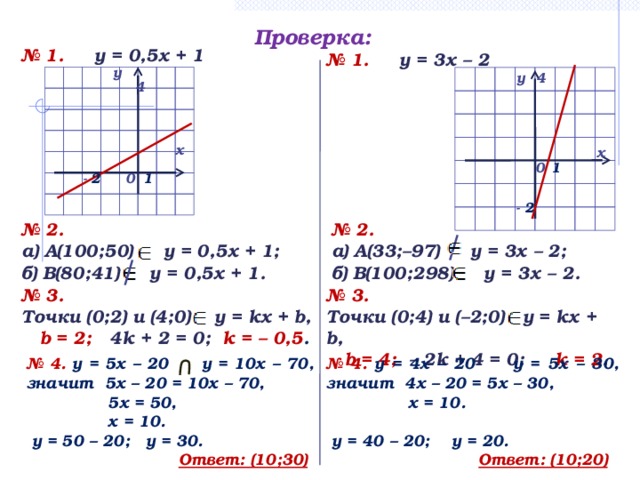
Дан график линейной функции у = kх+b (см. рис. 2). Определите числа k и b.
 рис. 2
рис. 2
Определите координаты точки пересечения графиков функций у = 4х – 20 и у = 5х – 30.
Вариант 1.
Постройте график функции у = 0,5х + 1.
Определите, принадлежит ли графику функции у = 0,5х + 1 точка:
а) А(100;50); б) В(80;41)
Дан график линейной функции у = kх+b (см. рис. 1). Определите числа k и b.
рис. 1
Определите координаты точки пересечения графиков функций у = 5х – 20 и у = 10х – 70.
у






1
-2
4
х
О
2
х
у
1
4
О
1
Проверка решения (ученики обмениваются тетрадями) (1-2 мин) (слайд 8)
Критерии оценивания (слайд 9)
Правильно выполнены задания 1 и 2 – «3»
Правильно выполнены задания 1, 2 и 3 – «4»
Правильно выполнены задания 1,2,3 и 4 – «5»
Итоги урока (1 мин)
Домашнее задание (1 – 2 мин) (слайд 10)
П. 6.3 учебника, № 518(б, г); 524; № 529 - по желанию.
Урок 5.
Тема урока: Линейная функция.
Тип урока: урок обобщения и повторения.
Цели урока:
обобщить и повторить учебный материал данной темы;
развивать вычислительные навыки;
развивать логическое мышление, умение анализировать, делать вывод;
Оборудование: Экран, компьютер, мультимедийный проектор, бланки для ответов.
Организационный момент.
Постановка цели урока.
Сегодня у нас с вами не совсем обычный урок, я предлагаю вам сыграть в «Свою игру»
Правила игры.
Класс делится на 3команды, выбирается капитан, название и девиз команды.
В результате жеребьевки определяется команда первая выбирающая вопрос, последующие вопросы выбирает команда, правильно ответившая на вопрос.
Ответ на вопрос готовится каждой командой и записывается в бланке ответов (Приложение 1)
Команда, капитан которой первый поднял руку, отвечает на вопрос, если ответ не правильный, то другие команды могут ответить на этот вопрос.
Проверка производится с помощью гиперссылки.
Очки присуждаются команде, правильно ответившей на вопрос.
Игра-презентация с гиперссылками «Своя игра». Учащиеся работают в группах.
Проводится жеребьевка.
Отгадайте слово, связанное с координатой точки на плоскости.
| 1 | 2 АБВГ | 3 ДЕЖЗ |
| 4 ИЙКЛ | 5 МНОП | 6 РСТУ ордината |
| 7 ФХЦЧ | 8 ШЩЪЫ | 9 ЬЭЮЯ |
Проводится игра.
Вопросы к игре.
А100 – Что называют функцией?
А200 – Что называют графиком функции?
А300 – Какую функцию называют линейной функцией?
А400 – Как найти координаты точки пересечения двух прямых?
Б100 – Какую функцию называют прямой пропорциональностью?
Б200 – Что является графиком функции y=b? Как называют эту функцию?
Б300 – В каком случае графики функций y1=k1x+b1 и y2=k2x+b2 параллельны?
Б400 – Графиком прямой пропорциональности является прямая, проходящая
через точку А(3;6). Задайте формулой эту функцию.
В100 – Какова область определения линейной функции?
В200 – Какой угол с осью X образует прямая y=kx+b при k
В300 – Расшифруйте слова и назовите лишнее: раяпмя, цуфняик, медиатр,
гунтмеар.
В400 – График функции вида y=kx – 0,5 параллельна графику функции
y= - 0,5x. Найдите k.
Г100 – В каких координатных четвертях расположен график функции
y=1,5x?
Г200 – Определите без построения, какие из графиков данных
функций пересекаются: y=5x, y=5 – 5x, y= - 5+x.
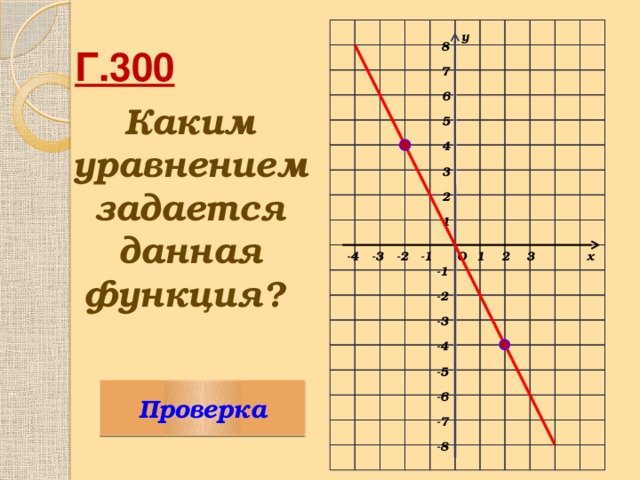
Г300 – Каким уравнением задается данная функция?
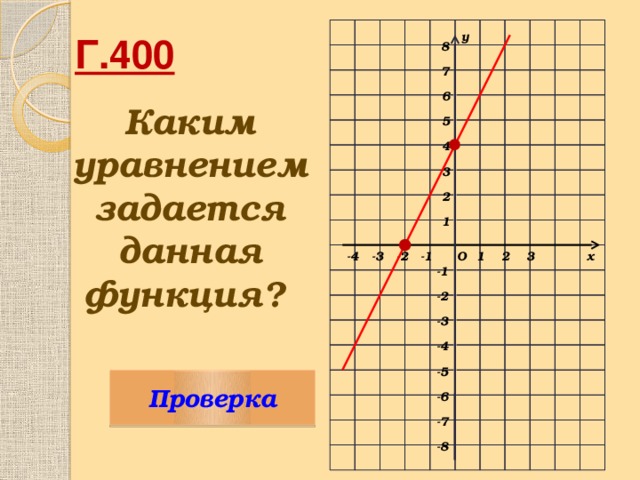
Г400 – Каким уравнением задается данная функция?
Жюри подводит итоги.
В конце игры оцениваются наиболее активные учащиеся.
Команды награждаются грамотами.
Приложение 1.
Бланк ответов
| № вопроса | Ответ на вопрос |
| 
| 100 |
|
| 200 |
|
| 300 |
|
| 400 |
|
| 
| 100 |
|
| 200 |
|
| 300 |
|
| 400 |
|
| 
| 100 |
|
| 200 |
|
| 300 |
|
| 400 |
|
| 
| 100 |
|
| 200 |
|
| 300 |
|
| 400 |
|
Список литературы.
Алгебра: учебник для 8 класса / С.М. Никольский, М. К. Потапов, Н.Н. Решетников, А.В. Шевкин – М.: Просвещение, 2009.
Алгебра. Дидактические материалы. 8 класс / М. К. Потапов, А.В. Шевкин – М.: Просвещение, 2009.
Уроки математики с применением информационных технологий 5-10 классы / Л.И. Горохова и др. – М.: Издательство «Глобус», 2010.
Сборник элективных курсов. Математика 8 – 9 классы/ В.Н. Студецкая, Л.С. Сагателова – Волгоград: Издательство «Учитель», 2006.
18
 рис. 1
рис. 1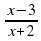 (х ≠ – 2); б)
(х ≠ – 2); б) 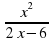 (х ≠ 3); в)
(х ≠ 3); в) 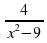 (х ≠ ±3); г)
(х ≠ ±3); г) 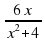 (х
(х R).
R).





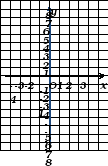 рис. 2
рис. 2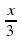 ; е) у = 2 – х;
; е) у = 2 – х;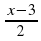 ; и) у = х.
; и) у = х.



 рис.3
рис.3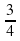 х
х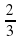 х
х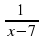 (х ≠ 7);
(х ≠ 7); 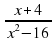 (х ≠ ±4); в) у = х2+ 8 (х
(х ≠ ±4); в) у = х2+ 8 (х


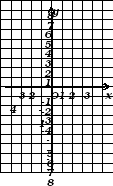 рис. 4
рис. 4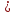 единиц влево, если р
единиц влево, если р 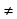
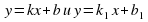 параллельны?
параллельны?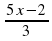 ; д) у =
; д) у = 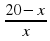 .
.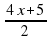 ; д) у = 2х2 + 1; е) у = 2х.
; д) у = 2х2 + 1; е) у = 2х.



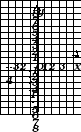
 рис. 2
рис. 2



 0 k Функцию вида у = kх называют прямой пропорциональностью, где х – переменная, k – угловой коэффициент. Построить графики функций : у Свойства : 8 7 а) у = 2х; б) у = - 3х. 1. Область определения 6 5 2. Графиком является прямая, проходящая через начало координат. 4 II I 3 2 3. Если k 0, график проходит через I и III четверть и образует острый угол с положительным направлением оси х. 1 -3 -2 -1 3 2 1 х -4 О -1 -2 III IV -3 4 . Если k -4 -5 -6 -7 -8" width="640"
0 k Функцию вида у = kх называют прямой пропорциональностью, где х – переменная, k – угловой коэффициент. Построить графики функций : у Свойства : 8 7 а) у = 2х; б) у = - 3х. 1. Область определения 6 5 2. Графиком является прямая, проходящая через начало координат. 4 II I 3 2 3. Если k 0, график проходит через I и III четверть и образует острый угол с положительным направлением оси х. 1 -3 -2 -1 3 2 1 х -4 О -1 -2 III IV -3 4 . Если k -4 -5 -6 -7 -8" width="640"
 1 график вытягивается вдоль оси у. 2. Если |k| вдоль оси х." width="640"
1 график вытягивается вдоль оси у. 2. Если |k| вдоль оси х." width="640"














 0 , или на |b| единиц вниз, если b 6 y = 2x; 5 4 y = 2x + 4; 3 y = 2x – 4. 2 1 х О 1 2 3 -2 -1 -3 -4 -1 -2 -3 -4 -5 -6 -7 -8" width="640"
0 , или на |b| единиц вниз, если b 6 y = 2x; 5 4 y = 2x + 4; 3 y = 2x – 4. 2 1 х О 1 2 3 -2 -1 -3 -4 -1 -2 -3 -4 -5 -6 -7 -8" width="640"
 0 , или на |р| единиц влево, если р 5 4 3 2 1 -4 4 х -1 -3 -2 -1 3 2 1 О -3 -1 -2 -3 -4 -5 -6 -7" width="640"
0 , или на |р| единиц влево, если р 5 4 3 2 1 -4 4 х -1 -3 -2 -1 3 2 1 О -3 -1 -2 -3 -4 -5 -6 -7" width="640"






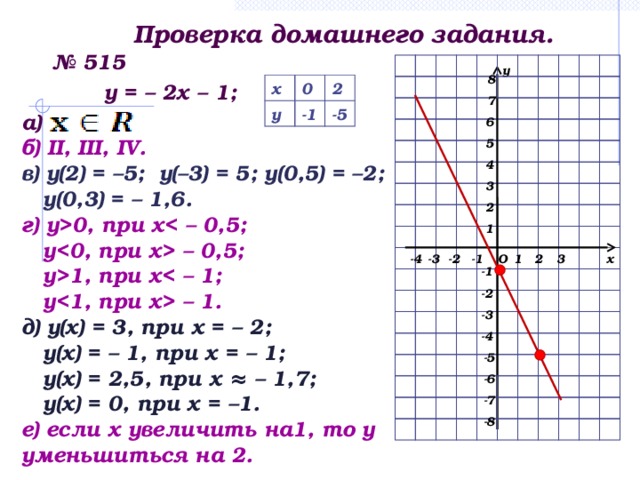 0, при х у – 0,5; у1, при х у – 1. д) у(х) = 3, при х = – 2; у(х) = – 1, при х = – 1; у(х) = 2,5, при х ≈ – 1,7; у(х) = 0, при х = –1. е) если х увеличить на1, то у уменьшиться на 2. 6 5 4 3 2 1 х О -3 1 3 -1 -2 -4 2 -1 -2 -3 -4 -5 -6 -7 -8" width="640"
0, при х у – 0,5; у1, при х у – 1. д) у(х) = 3, при х = – 2; у(х) = – 1, при х = – 1; у(х) = 2,5, при х ≈ – 1,7; у(х) = 0, при х = –1. е) если х увеличить на1, то у уменьшиться на 2. 6 5 4 3 2 1 х О -3 1 3 -1 -2 -4 2 -1 -2 -3 -4 -5 -6 -7 -8" width="640"