Жеребцова Галина Александровна
Решение комбинаторных задач.
Урок 1.
Цель: начать формировать умения решать простейшие комбинаторные задачи.
Задачи:
К концу урока учащиеся должны уметь:
Способствовать:
формированию познавательного интереса к предмету; мировоззрения учащихся.
воспитанию чувства патриотизма; ответственности за качество и результат, выполняемой работы.
совершенствованию операций умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать выводы, выделять существенные признаки.
ХОД УРОКА
I Актуализация опорных знаний.
Слово учителя: в старинных русских сказаниях повествуется, как богатырь или другой добрый молодец, доехав до распутья, читает на камне: “Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься”. Ребята, с какой проблемой сталкивается добрый молодец на перепутье?
Ответ учащихся: с проблемой выбора дальнейшего пути движения.
Слово учителя: Верно! А дальше уже говорится, как он выходит из того положения, в которое попал в результате выбора. Но выбирать разные пути или варианты приходится и современному человеку. Это сделать очень трудно не потому, что его нет или оно одно и поэтому его трудно найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций. И нам всегда хочется, чтобы этот выбор был оптимальный.
Оказывается существует целый раздел математики, именуемый комбинаторикой, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую.
II. Изучение нового материала.
Слово учителя: задачи, которые мы сегодня будем решать помогут вам творить, думать необычно, оригинально, смело, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое; преодолевать трудности и идти через невозможное вперед.
Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях объектов.
Учащимся раздаются цветные полоски (белый, синий, красный) и предлагается из них составить флаг РФ. Затем задаются вопросы исторического характера.

Что означает каждый цвет?
Значение цветов флага России: белый цвет означает мир, чистоту, непорочность, совершенство; синий – цвет веры и верности, постоянства; красный цвет символизирует энергию, силу, кровь, пролитую за Отечество.
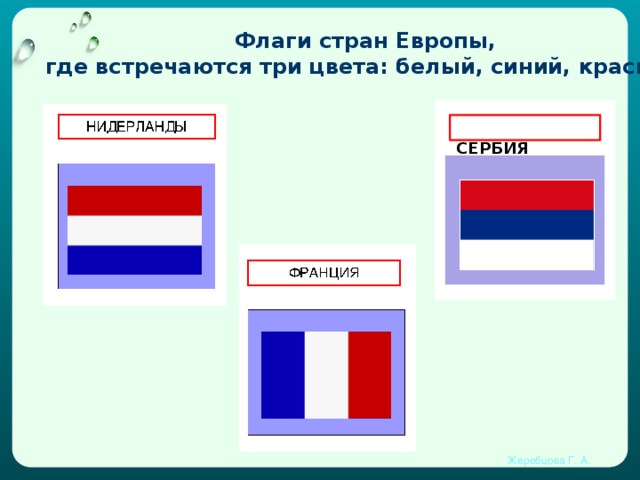
Оказывается, есть государства, где флаги имеют такие же цвета.
Флаги стран Европы, где встречаются три цвета: белый, синий, красный.
СЕРБИЯ



Видим, что от перестановок цветных полосок, можно получить другой флаг. Как подсчитать, сколько таких флагов мы можем составить из трех цветных полосок?
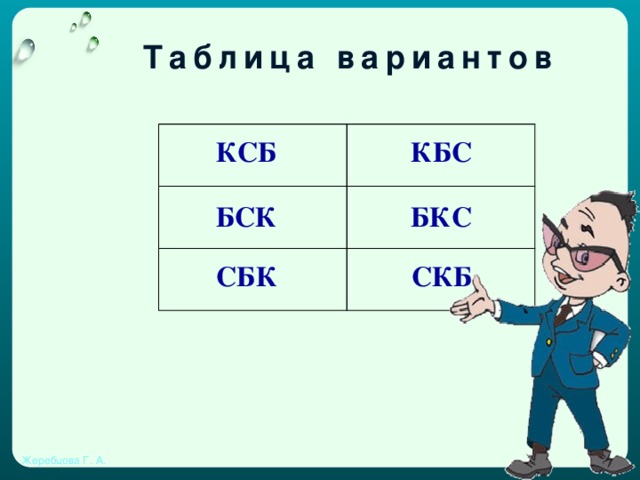
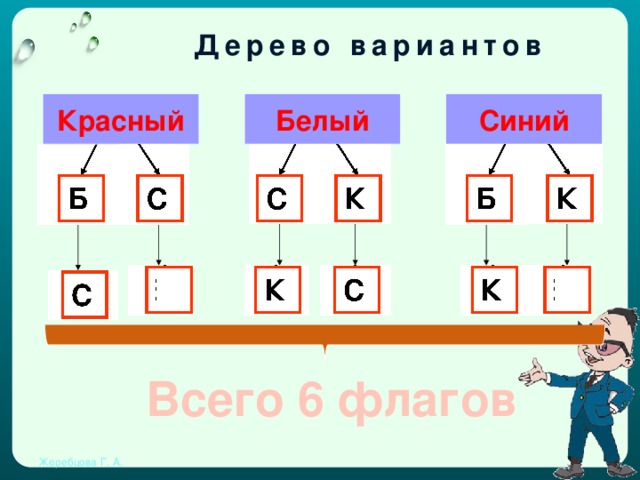
Решение этой задачи можно записать тремя способами:
Таблица вариантов
Дерево вариантов













Правило умножения
1 полоса 3 способа
2 полоса 2 способа
3 полоса 1 способ
3 ∙ 2 ∙ 1 = 6
Ответ: 6 способов
III Выполнение упражнений.
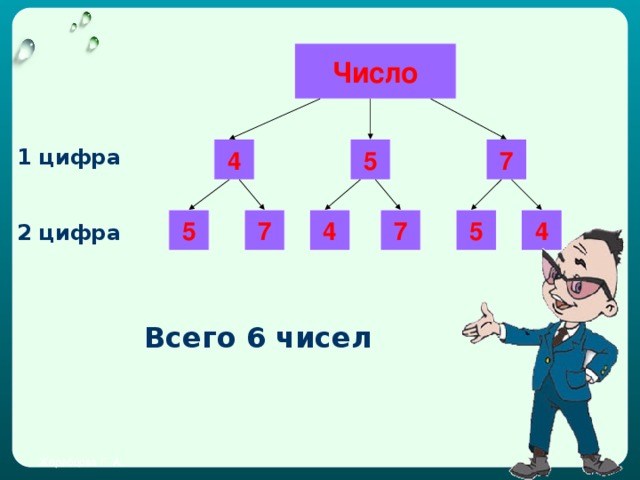
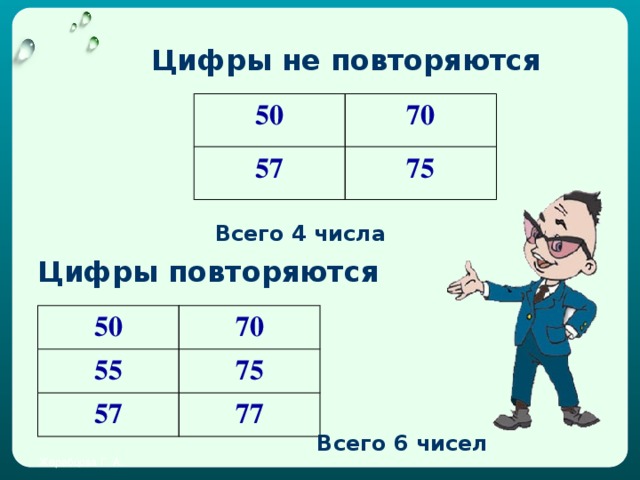
Сколько двузначных чисел можно составить, используя цифры 5, 7, 4, если известно, что цифры не повторяются (повторяются)?
Сколько двузначных чисел можно составить из цифр 5, 7 и 0?
IV Итог урока.
Домашнее задание.
Сколько трехзначных чисел можно составить из цифр 1, 3 и 5? Решите задачу различными способами
Урок 2.
Цель: продолжить формирование умений решать простейшие комбинаторные задачи практического содержания.
Задачи:
К концу урока учащиеся должны уметь:
учить учащихся находить возможные комбинации, составленные из чисел, слов, предметов, отвечающие условию задачи;
выяснить практическое применение математики в повседневной жизни.
Способствовать:
формированию познавательного интереса к предмету;
воспитывать чувство ответственности за качество и результат, выполняемой работы;
формированию сознательного отношения к труду.
развитию умения самостоятельно выбирать способ решения и умения обосновать выбор.
Из урока в урок я не перестаю повторять, а вы убеждаетесь в том, что наш мир полон математики. И сегодня мы продолжим исследовать на предмет выявления (если можно так выразиться) математики вокруг нас.
1) Устный опрос.
Какие задачи называются комбинаторными?
Что такое комбинаторика?
Может ли комбинаторика помочь в реальной жизни?
Как часто люди комбинируют?
Какими способами мы умеем решать комбинаторные задачи?
Ч чем заключается правило умножения?
В чем заключается правило решения задач с помощью дерева вариантов?
В каких играх мы применяем комбинаторику?
В это время два ученика оформляют на доске решение домашних задач.
2) Работа в группах.
Класс разбит на 5 групп. Каждая группа получает задания, на решение которых отводится 10 мин. После выполнения заданий каждая группа представляет свое решение.
1 группа.
В субботу в 5 «А» классе 5 уроков: физкультура, русский язык, литература, ИЗО, математика. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что математика – последний урок?
2 группа.
Путешественник хочет выехать на своей машине из города А, посетить города В, С и D, после чего вернуться в город А. Какими путями можно это сделать? На рисунке схема путей, связывающих города. Какой из вариантов самый оптимальный?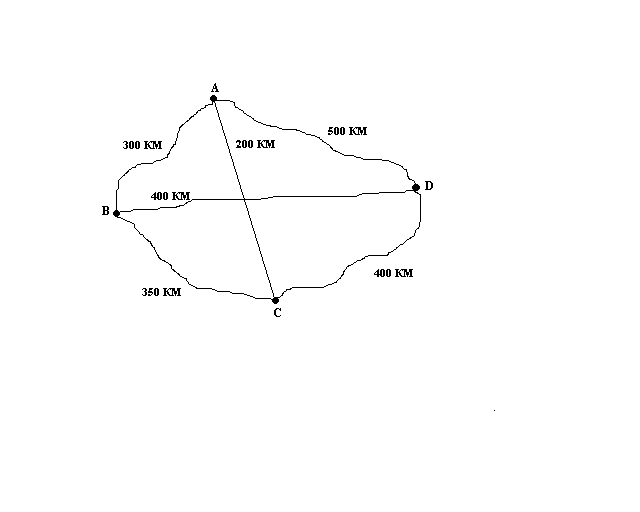
3 группа.
Участники лыжных соревнований стартуют с интервалом в 30 секунд. Чтобы определить порядок старта, спортсмены тянут жребий, определяющий номер старта. Сколько существует различных последовательностей выхода лыжников на старт, если в соревнованиях принимает участие 6 лыжников. Через какой промежуток времени все спортсмены будут на лыжне?
4 группа.
Проказница Мартышка,
Осел,
Козел,
Да косолапый Мишка
Затеяли сыграть в квартет.
Ударили в смычки, дерут, а толку нет.
………………..
«Стой, братцы, стой!» - кричит Мартышка.-
Погодите.
Как музыке идти? Ведь Вы не так сидите!
Сколькими различными способами могут сесть крыловские музыканты в один ряд?
5 группа.
Хоккейная комбинация. На поле 5 игроков. Начал комбинацию игрок № 1, продолжили игроки с другими номерами, а забил гол игрок № 5. Каждый хоккеист ударил по шайбе только один раз. На рисунке с помощью стрелок изображен один из возможных вариантов передачи шайбы между игроками в данной комбинации. Изобразите в тетради все другие возможные варианты передачи шайбы.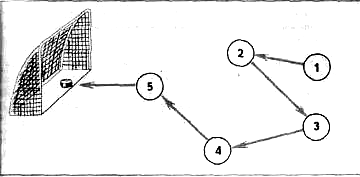
3) Представление решений.
4) Итоги
5) Домашнее задание.
а) Решить любые три задачи.
1. Сколько трёхзначных чисел можно составить, используя цифры 3 и 5?
2. Андрей зашел в магазин, чтобы купить майки. В магазине оказались майки четырех цветов: белые, голубые, красные, черные.
а) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки?
Подсказка: обозначьте цвета маек буквами Б, Г, К, Ч. Составьте дерево возможных вариантов
б) Сколько вариантов покупки есть у Андрея, если он хочет купить две майки разного цвета?
3. В классе три человека хорошо поют, двое других играют на гитаре, а еще один умеет показывать фокусы. Сколькими способами можно составить концертную бригаду из певца, гитариста и фокусника?
4. Наташа сшила кукле десять разных платьев, а Даша сшила своему мишке трое штанишек и четыре футболки. Как вы думаете, у кого больше разных нарядов – у куклы или у мишки?
5. Для начинки пирогов у Наташи есть капуста, яйца, зелень лук и клубничное варенье. Сколько различных начинок можно приготовить из этих продуктов? При этом не надо забывать, что пироги должны быть вкусными. Вряд ли кто из вас захочет съесть пирог с начинкой из капусты с клубничным вареньем.
6. Служитель зоопарка должен дать зайцу два различных овоща. Сколькими различными способами он может это сделать, если у него есть морковь, свекла и капуста?
7. В алфавите племени УАУА имеются всего две буквы – «а» и «у». Сколько различных слов по три буквы в каждом можно составить, используя алфавит этого племени?
8. На завтрак Вова может выбрать плюшку, бутерброд, пряник или кекс, а запить их он может кофе, соком или кефиром.
Сколько различных вариантов завтрака может выбрать Вова?
б) Составить синквейн.
ПРАВИЛА НАПИСАНИЯ СИНКВЕЙНА
1 строчка – одно слово – название стихотворения, тема, обычно существительное.
2 строчка – два слова (прилагательные или причастия). Описание темы, слова можно соединять союзами и предлогами.
3 строчка – три слова (глаголы). Действия, относящиеся к теме.
4 строчка – четыре слова – предложение. Фраза, которая показывает отношение автора к теме в 1-ой строчке.
5 строчка – одно слово – ассоциация, синоним, который повторяет суть темы в 1-ой строчке, обычно существительное.
Комбинаторика
Интересная, непознанная.
Изучать, понимать, перебирать.
Присутствует во всех областях.
Вариативность.
Урок 3.
Цель: продолжить формирование умений решать простейшие комбинаторные задачи практического содержания.
Задачи:
К концу урока учащиеся должны уметь:
находить возможные комбинации, составленные из чисел, слов, предметов, отвечающие условию задачи.
Способствовать:
обобщению и систематизации знаний и умений учащихся по теме
формированию познавательного интереса к предмету;
формированию сознательного отношения к труду;
развитию математического мышления и логической речи учащихся;
развитие умения самостоятельно выбирать способ решения и умения обосновать выбор.
1) Из истории науки «Комбинаторика» (сообщение ученика)
Комбинаторика – ветвь математики, изучающая комбинации и перестановки предметов, - возникла в XII веке.
Еще в доисторическую эпоху люди сталкивались с комбинаторными задачами. Выбирать и расположить предметы в определенном порядке, отыскивать среди разных рассположений наилучшее – вот задачи, решаемые в быту, на охоте или в сражениях. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. По мере усложнения производственных и общественных отношений задачи усложнялись. Комбинаторные задачи встречались, как игры в досуге. Наряду с состязаниями в беге, метании диска, кулачными боями появлялись игры, требовавшие умение мыслить, рассчитывать, составлять планы, опровергать планы противника. Со временем игры усложнились: появились нарды, карты, шашки и шахматы. В таких играх приходилось рассчитывать различные ситуации, комбинации сочетания фигур.
При тайных переписках дипломаты стали применять шифры, которые были основаны на различных перестановках букв, чисел, заменах букв с использованием ключевых слов и т. д.
Комбинаторика как наука стала развиваться в XIII в. параллельно с возникновением теории вероятностей. Первые научные исследования по этой теме принадлежат итальянским ученым Дж. Кардано, Н. Чарталье (1499-1557), Г. Галилею (1564-1642) и французским ученым Б.Пискамо (1623-1662) и П. Ферма. Комбинаторику, как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика». Значительный вклад в развитие комбинаторики внес Л. Эйлер. Современная символика сочетаний была предложена разными авторами учебных руководств только в XIX в.
За последние годы комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач, в частности задач по составлению расписаний; для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т. д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах — теории групп и их
представлений, изучении оснований геометрии, неассоциативных алгебр и т. д.
2) Повторение
Какие способы решения комбинаторных задач мы знаем?
Дерево вариантов, табличный, правило умножения.
Сравним эти способы.
| Способ решения | Плюсы | Минусы |
| Дерево вариантов | Наглядность, возможность увидеть все варианты | Очень громоздкий и длительный, если много различных вариантов |
| Табличный | Наглядность, компактность, возможность увидеть все варианты | Невозможность решать задачи, в которых более двух составляющих одного события |
| Правило умножения | Компактность, быстрота решения | «Не видно» самих вариантов, можно только просчитать их количество. |
3) Выполнение упражнений.
1. Туристическая фирма планирует посещение туристами в Италии трех городов: Венеции, Рима и Флоренции. Сколько существует вариантов такого маршрута?
2. Человек, пришедший в гости, забыл код, открывающий дверь подъезда, но помнил, что он составлен из нулей и единиц и содержит четыре цифры. Сколько вариантов кода в худшем случае ему придется перебрать, чтобы открыть дверь?
3. Витя, Толя и Игорь купили вместе интересную книгу и решили ее читать по очереди. Выпишите все варианты такой очереди. Сколько есть вариантов, в которых Игорь на первом месте? Витя не на последнем месте?
4. Имеется ткань двух цветов: голубая и зеленая – и требуется обить диван, кресло и стул. Сколько существует различных вариантов обивки этой мебели?
3) Самостоятельная работа.
| 1 вариант. 1. Сколько можно составить четырехзначных чисел из цифр 1, 5, 8, 3, если: а) цифры в числе не повторяются; б) цифры могут повторяться. 2. В среду в 5 «Б» классе 5 уроков: русский, информатика, естаствознание, ИЗО, иностранный. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что информатика –первый урок? | 2 вариант. 1. Сколько можно составить трехзначных чисел из цифр 4, 9, 7, если: а) цифры в числе не повторяются; б) цифры могут повторяться. 2. В среду в 5 «А» классе 5 уроков: русский, литература, естаствознание, математика, иностранный. Сколько можно составить вариантов расписания на день? Сколько можно составить вариантов расписания на день, зная, что математика – второй урок? |
4) Итог урока.
Математика повсюду –
Глазом только поведешь
И примеров сразу уйму
Ты вокруг себя найдешь…
5) Домашнее задание
Составить комбинаторные задачи практического содержания.
![]()
7