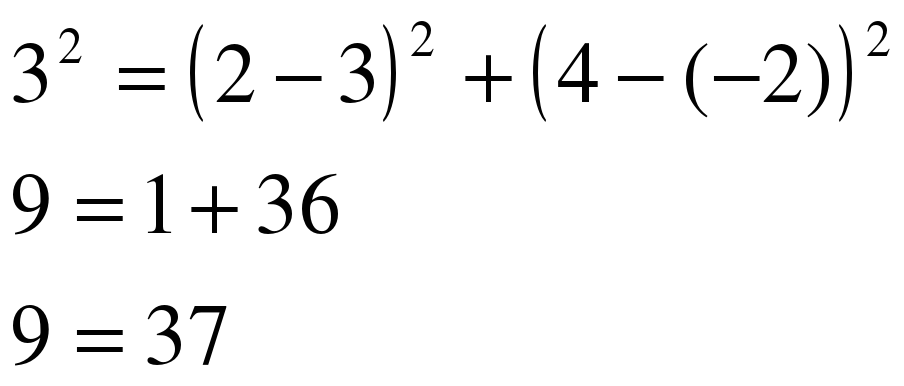.Цели урока:
– Распознать уравнение окружности по предложенному уравнению, научить учащихся составлять уравнение окружности по готовому чертежу, строить окружность по заданному уравнению.
– Видеть проблему и наметить пути её решения.
– Кратко излагать свои мысли устно и письменно.
| Этап урока | Деятельность учителя | Деятельность обучающихся |
| 1.Организационный момент. 2 мин
Цель данного этапа: Психологический настрой учащихся; Вовлечение всех учащихся в учебный процесс, создание ситуации успеха. | Включение в деловой ритм. Как сказал персидский философ Саади: «Ученик, который учится без желания – это птица без крыльев». И мне хотелось, чтобы у вас было желание учиться, узнавать что-то новое, неопознанное не только на сегодняшнем уроке, а всегда и только в этом случае своими «крыльями» будете «взлетать» все выше и выше. И пусть девизом к сегодняшнему уроку будут слова древнегреческого математика Фалеса: - Что есть больше всего на свете? – Пространство. - Что быстрее всего? – Ум. - Что мудрее всего? – Время. - Что приятнее всего? – Достичь желаемого. Хочется, чтобы каждый из вас на сегодняшнем уроке достиг желаемого резурезультата.
| Подготовка класса к работе.
|
| 2.Актуализация знаний. 5 мин
Цель этапа – получить представление о качестве усвоения учащимися материала, определить опорные знания. | Ведёт подводящий диалог. Фронтальная работа с классом
|
|
Даны координаты двух точек А(2;7) ; В(--2;7). Найдите: Координаты вектора 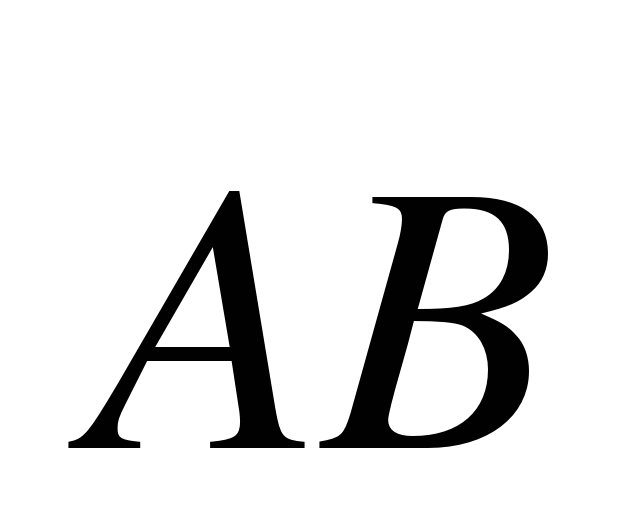 , , Длину вектора 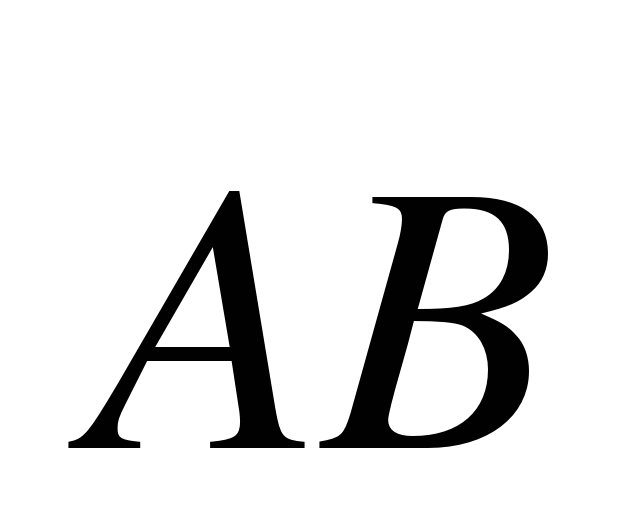 , , Расстояние между точками А и В.
| Вспоминают формулы и алгоритмы определения координат вектора, его длины, расстояния между двумя точками. Выполняют задания, тренирующие мыслительные операции и учебные навыки. Принимают участие в диалоге. Излагают своё мнение.
|
Определите, принадлежит ли точка К(3;1) графику функции y = 4x – 11? | Вспоминают алгоритм определения принадлежности точки графику функции. |
Что для этого надо сделать? | y = 4·3 – 11 = 1, да, принадлежит. |
Что является графиком данной функции? | Прямая |
| 3. Постановка учебной задачи 1 мин
Цель: выявление места и причины затруднения, постановка задач урока.
| Пробное действие: Принадлежит ли точка А(2;4) окружности с центром в точке К(3;-2) и радиусом 3?
| Самостоятельно пробуют решить задание. |
Что вызвало у вас затруднение? | Нет уравнения, в которое надо подставлять координаты точки.
|
Значит, какова ваша задача на сегодняшний урок? | Узнать уравнение окружности. |
| Запишите тему урока «Узнать уравнение окружности» |
|
| 4.«Открытие» детьми нового знания. 12 мин
Цель: построение детьми нового способа действий и формирование способности к его выполнению.
| С окружностью вы познакомились ещё в 5 и 8 классах. А что вы о ней знаете?
| Это геометрическая фигура, все точки которой равноудалены от данной точки. |
| Как называется эта данная точка? | Эта точка называется центром окружности. |
| Как называется расстояние от центра до любой точки окружности. | Радиусом |
| Историческая справка про окружность Древние греки считали окружность совершеннейшей и «самой круглой» фигурой. И в наше время в некоторых ситуациях, когда хотят дать особую оценку, используют слово «круглый», которое считается синонимом слова полнейший. Еще в древности людям были известны многие геометрические фигуры, в том числе окружность. Об этом свидетельствуют археологические раскопки. Окружность – самая простая кривая линия
|
|
| Начертите прямоугольную систему координат с началом в точке О(0;0) /Учитель строит на доске/ На данной системе координат произвольно отметьте точку А. Пусть ее координаты (а; в) /Учитель отмечает точку на построенной СК/ Постройте окружность произвольного радиуса с центром в точке А. /Учитель строит окружность/ Возьмите на окружности любую точку и обозначьте ее С. Пусть координаты данной точки будут (x; y) /Учитель на окружности берет точку, обозначает ее и записывает ее координаты/
| Учащиеся последовательно выполняют озвученные учителем действия. |
| У нас в СК есть две точки С и А. Что можно найти? | Расстояние между ними. |
| По какой формуле? | 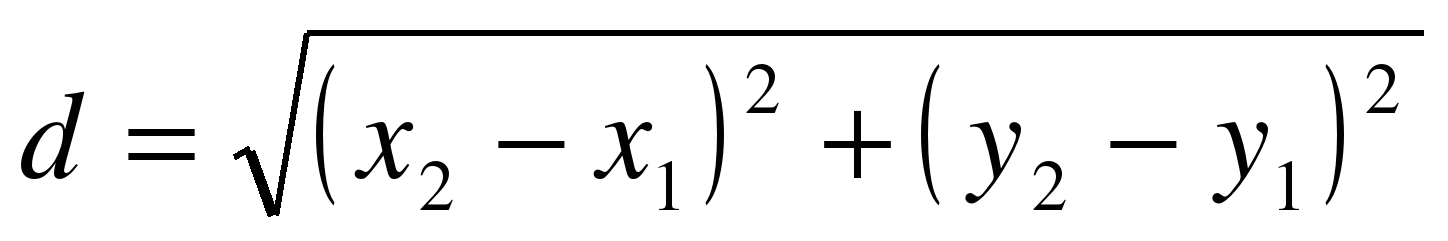
|
| Найдите расстояние между точками С и А. | 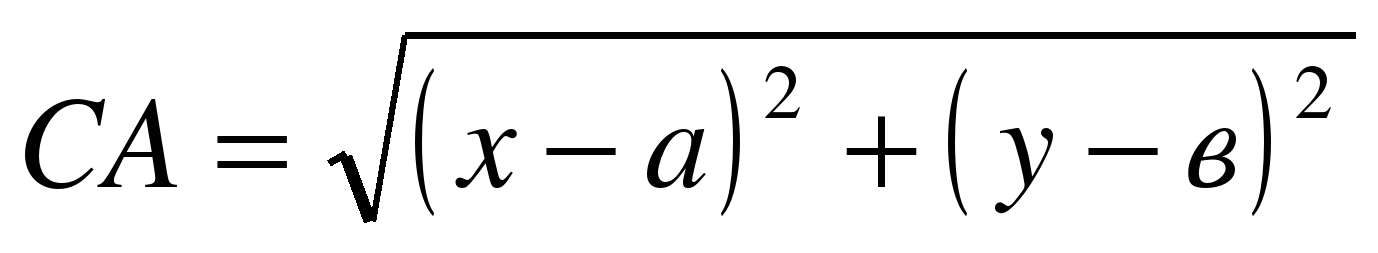
|
| Чем для окружности является расстояние СА? | Радиусом. |
| Какой буквой обозначается радиус? | r |
| Замените в равенстве СА и избавьтесь от квадратного корня. Что надо сделать для этого? | Возвести обе части уравнения в квадрат. |
| Что у вас получилось? | 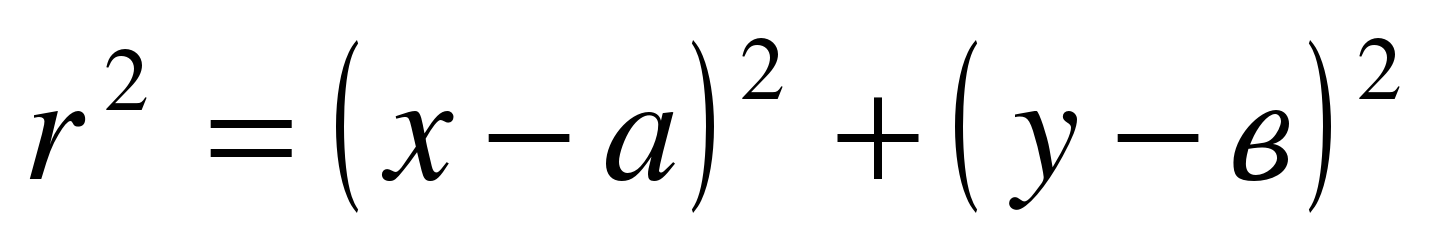 (1) (1)
|
| Что же это такое? | Уравнение окружности |
| А теперь вернемся к пробному действию: Принадлежит ли точка А(2;4) окружности с центром в точке К(3;-2) и радиусом 3? |
|
| Как будем делать? | Вместо (x0; y0) подставляем координаты точки К (3; -2); вместо (x; y) подставляем координаты точки А(2;4), а вместо r подставляем 3. Получается 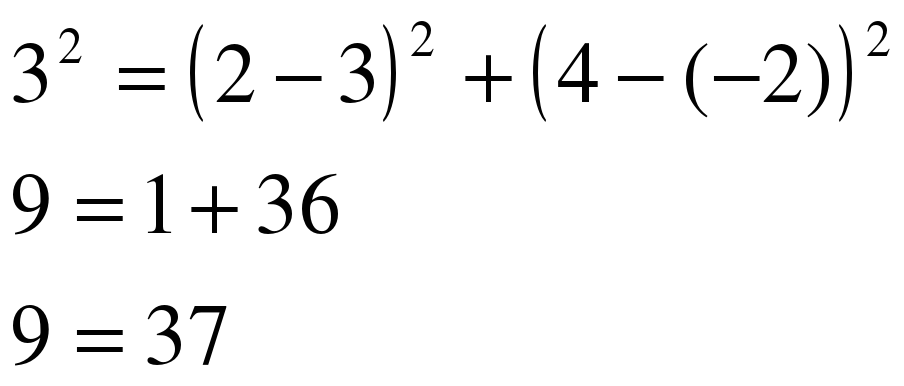
Равенство неверное, значит, точка А не принадлежит окружности с центром в точке К и радиусом 3. |
| Решите задачу: Какой вид будет иметь уравнение окружности с центром в начале координат?
Итак, что надо знать для составления уравнения окружности? Предложите алгоритм составления уравнения окружности.
Вывод: … записать в тетрадь.
ФИЗМИНУТКА | (0;0)-координаты центра окружности. х²+у²=r², где r-радиус окружности.
-координаты центра окружности, радиус, любую точку окружности… Предлагают алгоритм… Записывают алгоритм в тетрадь. |
| 4.Первичное закрепление 10 мин
Цель: усвоение нового способа действий.
| Применим полученные знания при решении следующих задач. Задача: Определите, является ли данное уравнение уравнением окружности и если да, то найдите радиус и диаметр.
-Не каждое уравнение второй степени с двумя переменными задаёт окружность. 4х²+у²=4-уравнение эллипса. х²+у²=0-точка. х²+у²=-4-это уравнение не задаёт никакой фигуры.
Фронтальная работа у доски.
Решите задачу №966(а) стр.241(учебник). Учитель вызывает ученика к доске. -Достаточно ли данных, которые указаны в условии задачи, чтобы составить уравнение окружности? (да)
Задача: Напишите уравнение окружности с центром в начале координат и диаметром 8.
Задача: построение окружности. - Центр имеет координаты? - Определите радиус… и выполняйте построение
Фронтальная работа у доски.
|
4х²+у²=4-не является уравнением окружности. х²+у²=0- не является уравнением окружности. х²+у²=-4- не является уравнением окружности.
а) А(0; 5) – центр окружности, r=3 1. x0 = 0, y0 = 5 2. r=3 3. 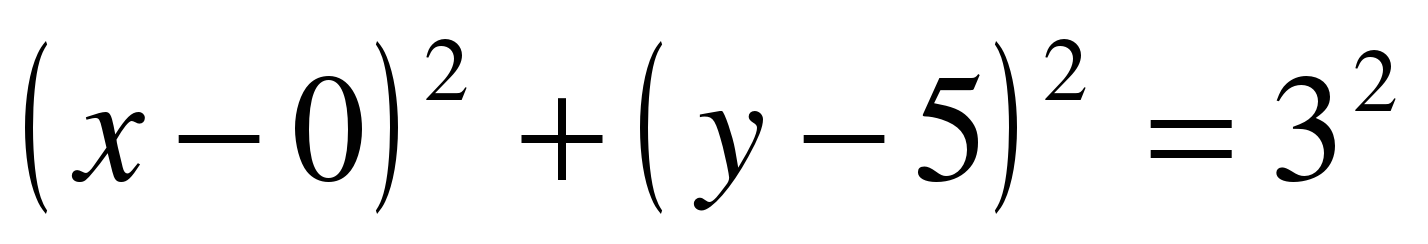 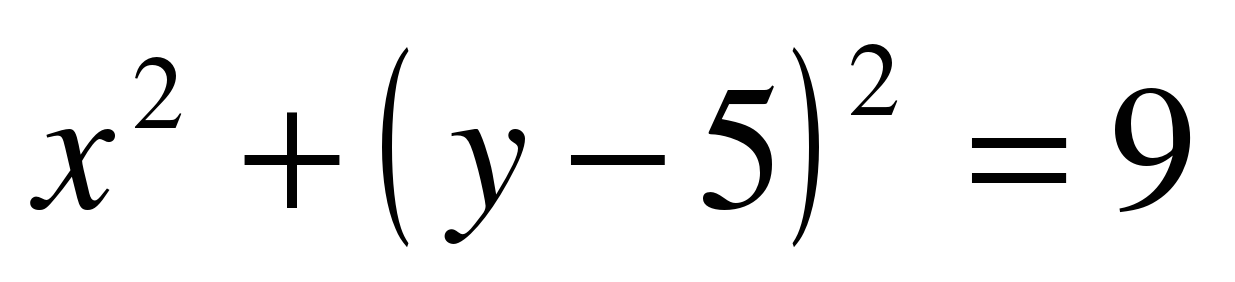 - уравнение искомой окружности. - уравнение искомой окружности.
-Так как диаметр окружности в два раза больше её радиуса, то r=8÷2=4. Поэтому х²+у²=16.
- Выполняют построение окружностей 
|
| Еще раз озвучьте введенный алгоритм. Задача на стр.243(учебник) разбирается устно. Используя план решения задачи со стр.243, решите задачу: Составьте уравнение окружности с центром в точке А(3;2), если окружность проходит через точку В(7;5).
| Работа по учебнику. Задача на стр.243. Дано: А(3;2)-центр окружности; В(7;5)є(А;r) Найти: уравнение окружности Решение r² =(х –х )²+(у –у )² r² =(х –3)²+(у –2 )² r = АВ, r² = АВ² r² =(7-3)²+(5-2)² r² =25 (х –3)²+(у –2 )²=25 Ответ: (х –3)²+(у –2 )²=25
|
| 6. Самостоятельная работа с самопроверкой 10-12 мин Цель: контроль ЗУН
|
В задачах составить уравнения окружности по готовым чертежам
Заполнить таблицу:  Практическая работа. Задание 1: Записать своё ФИО в тетради, подсчитать количество букв в каждом слове и записать над словом. Число, которое соответствует фамилии – значение а, имени – b и отчеству – R. Составьте уравнение окружности по данным значениям и начертите окружность в системе координат. **Задание 2: В системе координат нарисуйте снеговика. Найдите центр и радиус каждой окружности и запишите её уравнение.
|
|
| 7.Рефлексия деятельности (итог урока) 2 мин
Цель: самооценка результатов деятельности, осознание метода построения, границ применения нового знания.
|
-О чём на уроке мы говорили? -Что хотели получить? -Какая цель была поставлена на уроке? -Какие задачи позволяет решить сделанное нами «открытие»?
| Проводят рефлексию и самооценку своей деятельности на уроке. Высказываются мнения. Узнать уравнение окружности |
| 8.Домашнее задание 2 мин | Домашнее задание: §3, п.94, контрольные вопросы №16,17. Задачи № 959(б, г, д), 967. Дополнительная задача (проблемная задача): Построить окружность, заданную уравнением х²+2х+у²-4у=4. Оценивание работы уч-ся на уроке.( объявить оценки учащимся) У каждого из вас на столе карточки (красная, зелёная, жёлтая). Уходя из класса, прикрепите на магнитную доску одну из них. До свидания! Спасибо за урок! Карточка красного цвета обозначает: “Я удовлетворён уроком, урок был полезен для меня, я много, с пользой и хорошо работал на уроке, я понимал всё, о чём говорилось и что делалось на уроке”. Карточка желтого цвета: «В целом материал мне понятен, но остались вопросы» Карточка зеленого цвета: «Я ничего не понял»
| Записывают домашнее задание.
На выходе из класса учащиеся крепят на магнитной доске карточку выбранного цвета
|