Тема: «Вероятность равновозможных событий».
Автор: Мухаметгалиева Эльвира Наиловна
МБОУ «Кушарская ООШ» Атнинского муниципального района
Класс: 9
Тип урока: урок обобщения и систематизации знаний.
Цель урока:
Задачи урока:
повторить, что такое вероятность;
рассмотреть задания из тренировочных тестов ГИА, ЕГЭ по данной теме;
развивать элементы логического мышления, речь, память, мышление;
воспитывать познавательный интерес к предмету, расширять кругозор.
План урока:
1. Организационный момент.
2. Актуализация знаний.
3. Обобщение и систематизация знаний.
4. Проверка знаний.
5. Домашнее задание.
6. Итоги урока.
Ход урока
1. Организационный момент. ХАЙ ФАИВ
Применяю структуру МЭНЭДЖ МЭТ.
Учащиеся рассаживаются по 4 человека за столы, образуя команды.
Сообщить тему урока и сформулировать цели урока.
2. Актуализация знаний.
Применяю структуру СИНГЛ РАУНД РОБИН (обучающая структура, в которой учащиеся проговаривают ответы на данный вопрос по кругу один раз).
Какие виды событий вы знаете?
Из курса математики 5-6 класса известны 3 вида событий:
- достоверное (вероятность такого события равна 1);
- невозможное (вероятность такого события равна 0);
- случайное (вероятность такого события от 0 до 1).
Вероятностью Р наступления случайного события А называется отношение 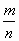 , где n - число всех возможных исходов эксперимента, а m - число всех благоприятных исходов события А:
, где n - число всех возможных исходов эксперимента, а m - число всех благоприятных исходов события А:
P (A) =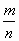
3. Обобщение и систематизация знаний.
Применяю структуру ФИНК-РАЙТ-РАУНД-РОБИН (« подумай – запиши - обсуди в команде». Во время выполнения данной структуры участники ОБДУМЫВАЮТ высказывание или ответ на какой-либо вопрос, ЗАПИСЫВАЮТ и по очереди ОБСУЖДАЮТ свои ответы в команде.).
Каждый ученик получает задание, думает (вспоминает определение), записывает решение, обсуждают в команде.
Задачи из тестов ГИА.
1. При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих кубиках выпадут одинаковые числа? Вероятность: P(A)=6/36=1/6.
2. Из 50 детей детского дома 18 были на Ёлке в Кремле, 12 - на Ёлке в цирке, а остальные посетили Ледовое шоу в Лужниках. Какова вероятность, что случайно выбранный ребенок был в Лужниках? Ответ: 2/5=0,4
3. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру. Найдите вероятность того, что начинать игру должен будет мальчик. Ответ: 0,4.
4. Из класса, в котором учатся 10 мальчиков и 15 девочек, выбирают по жребию одного дежурного. Какова вероятность того, что это будет девочка? Ответ: 15/25=0,6
5. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5? Ответ: 0,2.
6. Из ящика, где хранятся 17 желтых и 14 красных шаров, продавец, не глядя, вынимает один шар. Какова вероятность того, что этот шар окажется желтого цвета?
1) 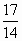 2)
2) 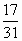 3)
3) 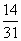 4)
4) 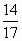 Ответ:
Ответ: 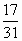
7. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен из Норвегии или Швеции. Ответ: 0,35.
8. Телевизор у Маши сломался и показывает только один случайный канал. Маша включает телевизор. В это время по трем каналам из двадцати показывают кинокомедии. Найдите вероятность того, что Маша попадет на канал, где комедия не идет. Ответ: 0,85.
9. Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер? Ответ: 0,18
10. В чемпионате по футболу участвуют 16 команд, которые жеребьевкой распределяются на 4 группы: A, B, C и D. Какова вероятность того, что команда России не попадает в группу A? Ответ: 0,75.
4. Проверка знаний.
Применяю структуру СИМАЛТИНИУС РАУНЛ ТЭЙБЛ
Учащиеся выполняют одновременно работу, потом по команде передают по кругу и проверяют по готовым кратким решениям.
Самостоятельная работа.
I-вариант
1. На семинар приехали 4 ученых из Италии, 6 из России и 5 из Норвегии. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что вторым окажется доклад ученого из России. Ответ: 0,4
2.Фабрика выпускает сумки. В среднем на 160 качественных сумок приходится четыре сумки со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых. Ответ: 0,98
3. Катя дважды бросает игральный кубик. В сумме у нее выпало 6 очков. Найдите вероятность того, что при втором из бросков выпало 5 очков. Ответ: 0,2
II-вариант
1. В среднем из 1500 садовых насосов, поступивших в продажу, 12 подтекают. Найдите вероятность того, что случайно выбранный для контроля насос не подтекает. Ответ: 0,992
2. В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам. Ответ: 0,55
3. Даша дважды бросает игральный кубик. В сумме у нее выпало 8 очков. Найдите вероятность того, что при одном из бросков выпало 2 очка. Ответ: 0,4
5. Домашнее задание.
В случайном эксперименте бросают три игральные кости. В сумме выпало 12 очков. Найдите вероятность того, что при первом броске выпало 3 очка. Результат округлите до сотых.
Даша трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут одинаковые числа.
6. Итоги урока.
- Что нужно знать для нахождения вероятности случайного события?
Для вычисления классической вероятности нужно лишь знать все возможные исходы события и благоприятные исходы. Однако в жизни чаще встречаются события, сравнить и оценить которые, основываясь только интуиции, невозможно и трудно. Классическое определение вероятности применимо только к событиям с равновозможными исходами, что ограничивает область его применения.
- Для чего в школе изучаем теорию вероятности?
Теория вероятностей – один из наиболее важных прикладных разделов математики. Многие явления окружающего нас мира поддаются описанию только с помощью теории вероятностей.
Спасибо за урок!
















