Пояснительная записка.
Построение сечений многогранников – тема не из легких, но на изучение отводится 2 – 3 урока.
В дальнейшем учащиеся сталкиваются с применением сечений на ЕГЭ, а также при изучении математики в ВУЗах. С помощью средств программы Power Point можно более наглядно представить данный материал, что способствует лучшему усвоению, формированию умений самостоятельного решения задач на построение сечений.
Данный урок по теме - №2. То есть, рассмотрены свойства тетраэдра и параллелепипеда, понятие секущей плоскости, свойства параллельных плоскостей и т.д.
Урок посвящен формированию и закреплению навыков построения сечений многогранников.
Цели урока.
- Повторить теоретический материал: секущая плоскость, пересечение плоскостей, пересечение плоскости и многоугольника, пересечение двух параллельных плоскостей третьей плоскостью, тетраэдр, параллелепипед. Формирование и закрепление навыков решения задач на построение сечений тетраэдра и параллелепипеда.
- Развитие логического мышления, пространственного воображения, умения применять изученный материал в нестандартных ситуациях. Развитие грамотной математической речи через теоретическое обоснование своих выводов. Повышение интереса к изучаемому предмету.
- Воспитание ответственного отношения к выполнению заданий, подготовке к уроку. Воспитание уважения к своим одноклассникам через умение слушать и слышать отвечающих, оказание помощи в трудных ситуациях.
Оборудование:
- ПК; проектор
- Классная доска;
- Школьные принадлежности ученика;
- Модели тетраэдра и параллелепипедов.
Просмотр содержимого документа
«Конспект урока геометрии»
Просмотр содержимого презентации
«к уроку. построение сечений»

Геометрия. 10 класс.
«Построение сечений».
Автор: учитель математики
МКОУ Брединской СОШ №2
Смирнова Галина Александровна.
Бреды. 2013.

ЦЕЛИ УРОКА:
- Повторить теоретический материал: секущая плоскость, пересечение плоскостей, пересечение плоскости и многоугольника, пересечение двух параллельных плоскостей третьей плоскостью, тетраэдр, параллелепипед. Формирование и закрепление навыков решения задач на построение сечений тетраэдра и параллелепипеда.
- Развитие логического мышления, пространственного воображения, умения применять изученный материал в нестандартных ситуациях. Развитие грамотной математической речи через теоретическое обоснование своих выводов. Повышение интереса к изучаемому предмету.
- Воспитание ответственного отношения к выполнению заданий, подготовке к уроку. Воспитание уважения к своим одноклассникам через умение слушать и слышать отвечающих, оказание помощи в трудных ситуациях.
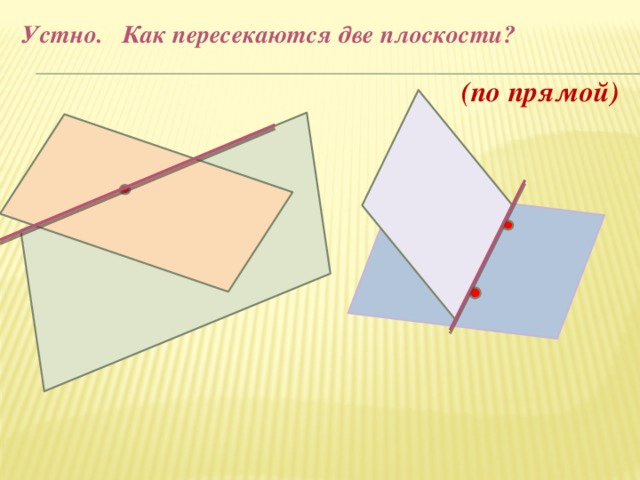
Устно. Как пересекаются две плоскости?
(по прямой)
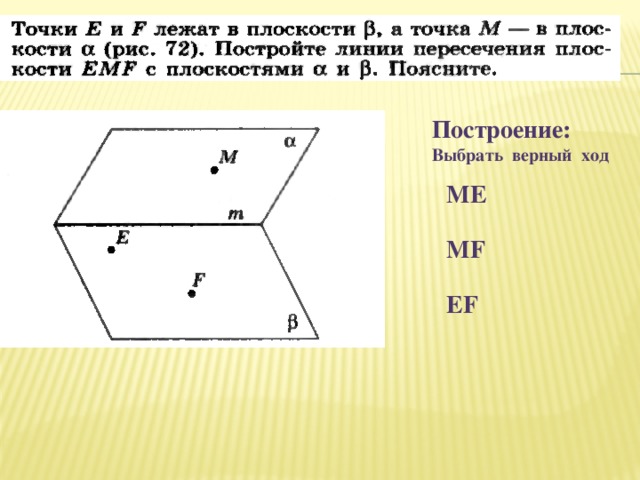
Построение:
Выбрать верный ход
МЕ
MF
EF
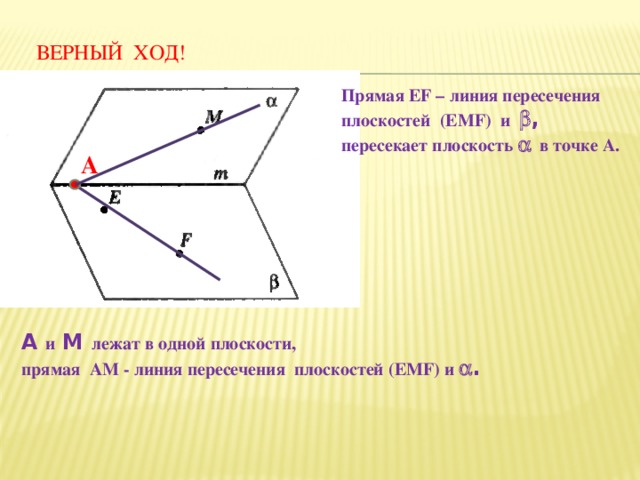
ВЕРНЫЙ ХОД!
Прямая EF – линия пересечения
плоскостей (EMF) и ,
пересекает плоскость в точке А.
А
А и М лежат в одной плоскости,
прямая АМ - линия пересечения плоскостей (EMF) и .
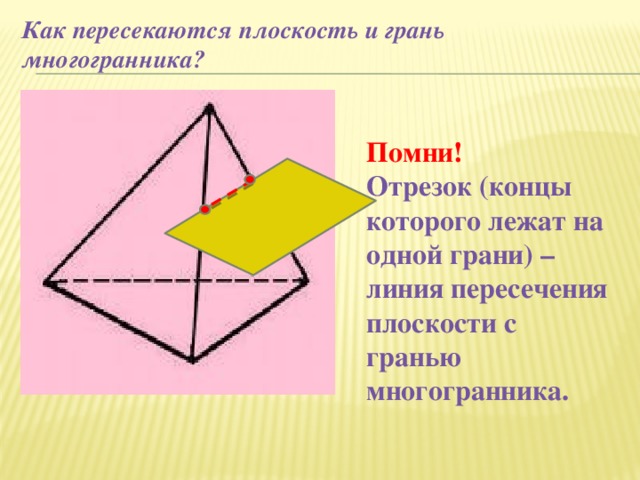
Как пересекаются плоскость и грань многогранника?
Помни!
Отрезок (концы которого лежат на одной грани) – линия пересечения плоскости с гранью многогранника.
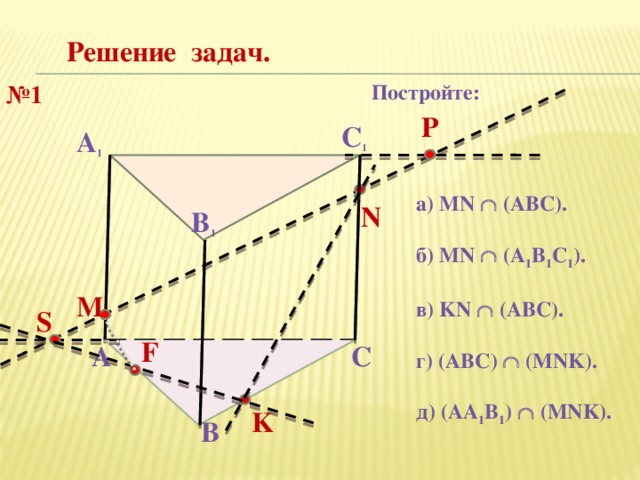
Решение задач.
Постройте:
№ 1
P
С 1
А 1
а) MN (ABC).
б) MN (A 1 B 1 C 1 ).
в) KN (ABC).
г) (АВС) (MNK).
д) (АA 1 B 1 ) (MNK).
N
В 1
М
S
F
А
С
K
В
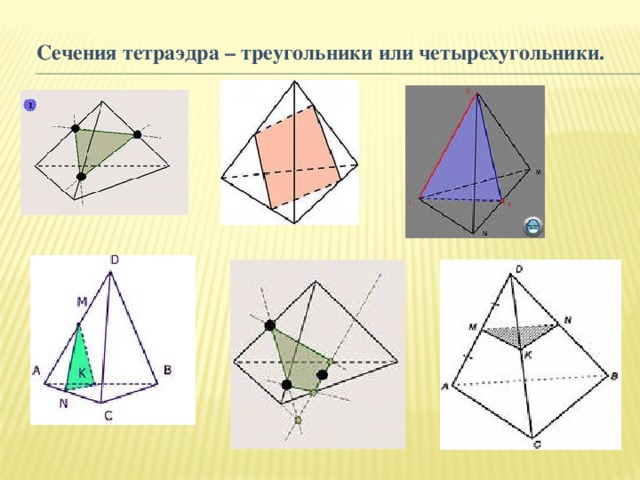
Сечения тетраэдра – треугольники или четырехугольники.
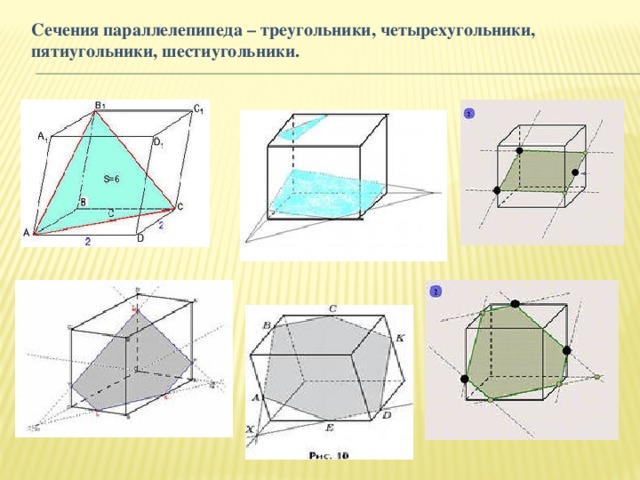
Сечения параллелепипеда – треугольники, четырехугольники, пятиугольники, шестиугольники.

Наши действия при построении сечения многогранника плоскостью.
- Соединим точки, принадлежащие одной грани.
- Дополним до прямых те ребра многогранника , которые при продолжении пересекутся с секущей плоскостью.
- Соединим точки, принадлежащие одной плоскости.
- Получим точки пересечения секущей плоскости и рёбер многогранника.
- Эти точки и будут вершинами многоугольника, являющегося искомым сечением.
Помним!
Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
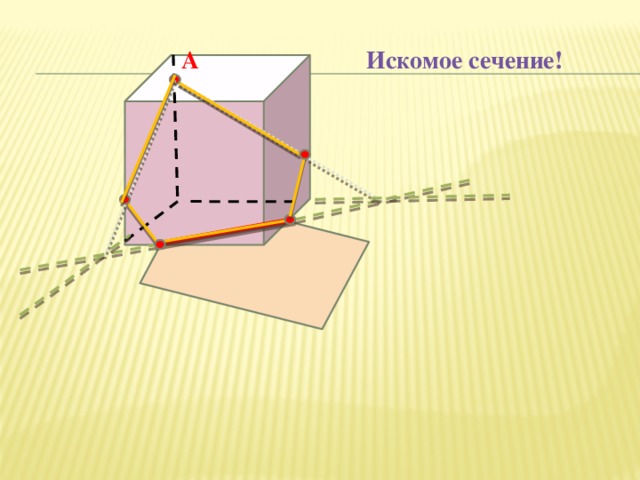
А
Искомое сечение!
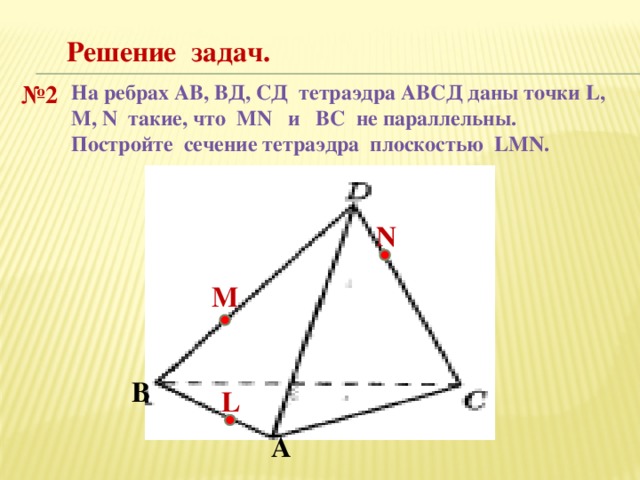
Решение задач.
№ 2
На ребрах АВ, ВД, СД тетраэдра АВСД даны точки L, M, N такие, что MN и ВС не параллельны. Постройте сечение тетраэдра плоскостью LMN.
N
М
В
L
А
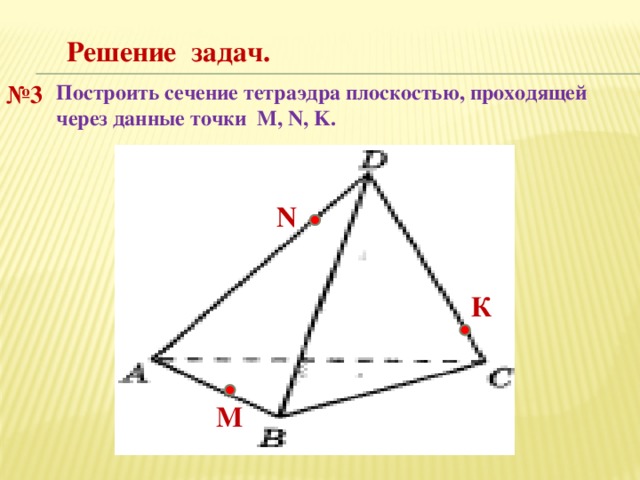
Решение задач.
№ 3
Построить сечение тетраэдра плоскостью, проходящей через данные точки M, N, K.
N
К
М
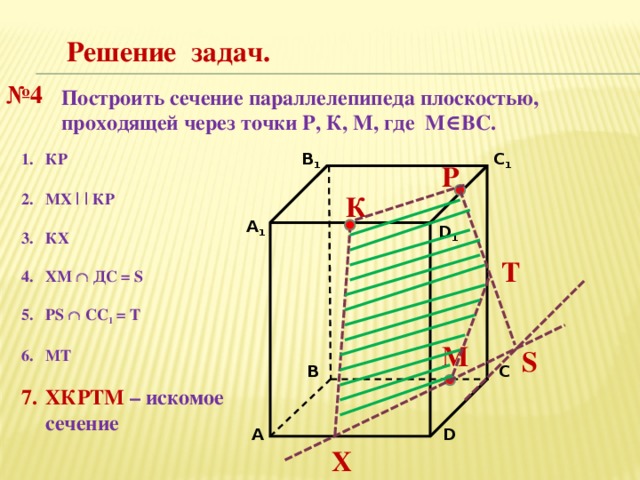
Решение задач.
№ 4
Построить сечение параллелепипеда плоскостью, проходящей через точки Р, К, М, где М∈ВС.
В 1
C 1
P
К
А 1
D 1
Т
М
S
С
В
D
А
Х
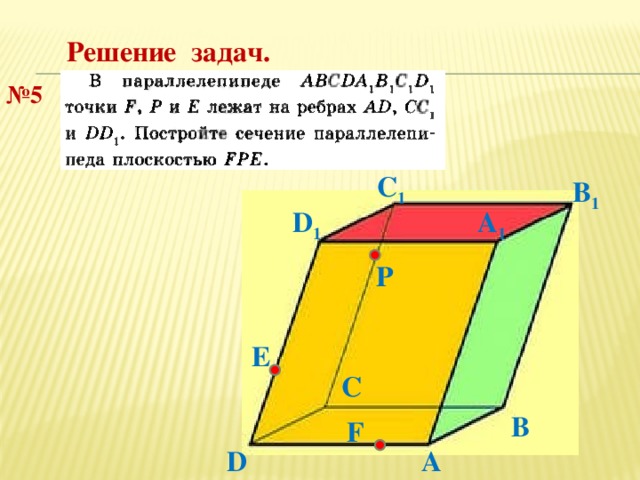
Решение задач.
№ 5
С 1
В 1
D 1
А 1
P
E
C
В
F
А
D
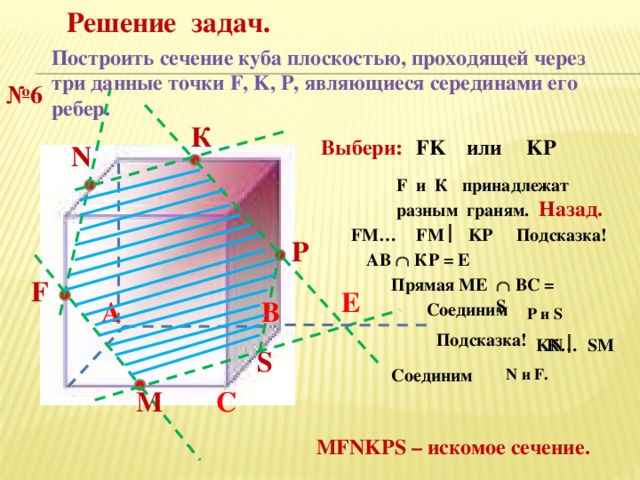
Решение задач.
Построить сечение куба плоскостью, проходящей через три данные точки F, K, P, являющиеся серединами его ребер.
№ 6
К
KP
Выбери:
FK
или
N
F и К принадлежат разным граням. Назад.
FM KP
Подсказка!
FM…
P
АВ КР = Е
Прямая МЕ
F
ВС = S
Е
В
А
Соединим
Р и S
Подсказка!
KN SM
К…
S
N и F.
Соединим
C
М
MFNKPS – искомое сечение.
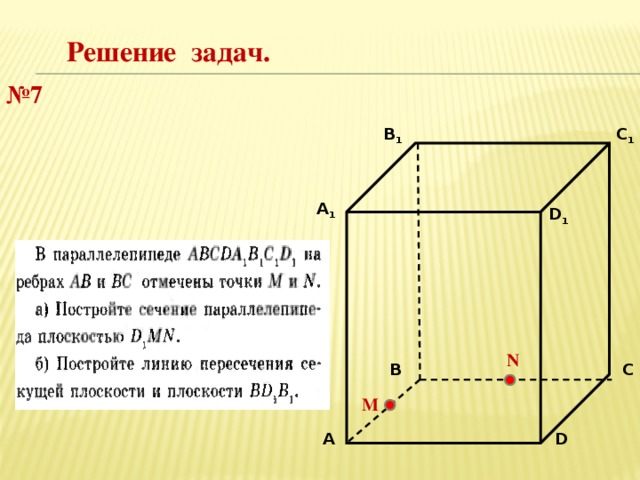
Решение задач.
№ 7
C 1
В 1
А 1
D 1
N
В
С
М
А
D
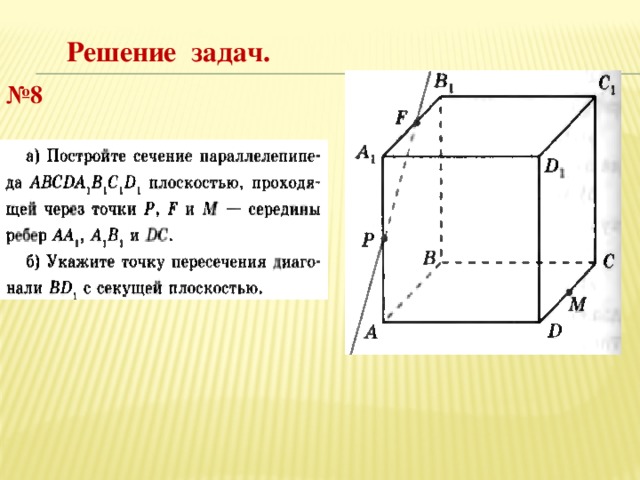
Решение задач.
№ 8
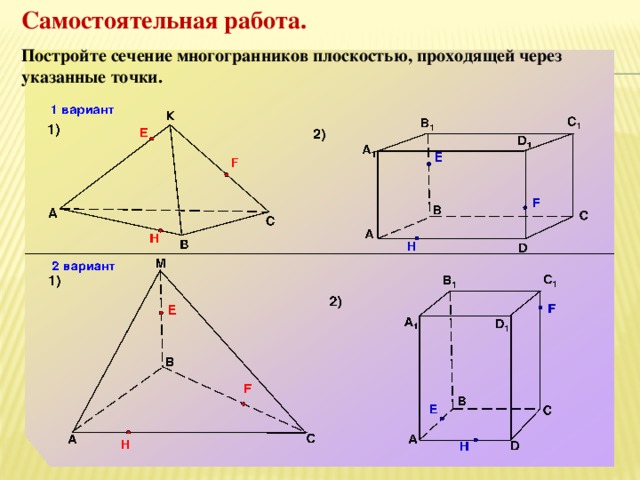
Самостоятельная работа.
Постройте сечение многогранников плоскостью, проходящей через указанные точки.

Точки M и E принадлежат разным плоскостям,
соединять нельзя.
НАЗАД

Точки M и F принадлежат разным плоскостям,
соединять нельзя.
НАЗАД

Назад.
Есть параллельные грани.

Домашнее задание.
- Повторить теоретический материал п. 12 – 14.

Итоги урока.
- Пересечением плоскостей является …
- Плоскость пересекает грань многогранника по …
- Сечением тетраэдра являются …
- Сечением параллелепипеда могут быть …
- Секущая плоскость пересекает параллельные грани по …
Что понравилось на уроке? Что осталось непонятым? На какие моменты выделить время на следующем уроке?

Литература:
- Геометрия 10 – 11. учебник для общеобразовательных учреждений. Авторы: Л.С.Атанасян и др. Москва, Просвещение, 2009г.
- Геометрия 10класс. Поурочные планы. Автор – составитель Г.И.Ковалева. Волгоград, изд. «Учитель» 2003г.
- Поурочные разработки по геометрии 10 класс. дифференцированный подход. Автор: В.А.Яровенко. Москва, «Вако», 2010г.
- Геометрия. 10класс. Дидактические материалы. Автор: Б.Г.Зив. Москва, Просвещение, 2009г.
- Изучение геометрии в 10 – 11 классах. Авторы: С.М. Саакян и В.Ф.Бутузов. Москва, Просвещение, 2010г.
- Геометрия 10. рабочая тетрадь. Авторы: Ю.А.Глазков, В.Ф.Бутузов. Москва, Просвещение, 2010г.