Конспект урока "Основные понятия теории вероятностей"

Материал полезен для подготовки к экзамену. В данном конспекте рассматривается вывод формулы классической вероятности и её применение при решении задач.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

=> ПОЛУЧИТЬ СУПЕРСПОСОБНОСТИ УЧИТЕЛЯ <=

Просмотр содержимого документа
«Конспект урока "Основные понятия теории вероятностей"»

Конспект урока математики

ФИО учителя	Название ОУ
Андреева Светлана Геннадьевна	МКОУ «Солодчинская СШ»

Класс	Тема	УМК
7	«Основные понятия теории вероятностей»	«Алгебра: 7 класс» под ред. А.Г.Мордковича

Основные дидактические цели урока:

организовать деятельность учащихся по открытию формулы классической вероятности;
сформировать представление о событии, исходе; познакомить учащихся со способом решения по формуле классической вероятности;
Сформировать у обучающихся навык использования формулы классической вероятностей.

Структура урока:

актуализация знаний учащихся
мотивация
открытие способа действия (формулы классической вероятности)
формирование способа действия - нахождение классической вероятности по формуле
динамичная пауза
закрепление
рефлексия

организационная структура (сценарий) урока

Визуальный ряд

Деятельность учителя

Деятельность учащихся

-Прочитайте предложение на слайде.

Проанализируйте в нём информацию.

-Замечательно. Внесите изменение в данное предложение, которое не изменит основной мысли.

-Какие оценки преобладали у Кати?

-Сколько всего было написано самостоятельных работ?

-Сколько было пятёрок?

-Сколько было четвёрок?

-К какой группе учеников вы отнесёте Катю: к успевающим на «4» и «5», к обучающимся на «удовлетворительно», к ученикам, имеющим трудности в освоении данного предмета?

-[По щелчку на триггер (прямоугольник голубого цвета) открывается вопрос задачи] Ответьте теперь на вопрос нашей мудрой совы – Можно ли сказать, что следующую самостоятельную Катя напишет хорошо с большой вероятностью?

-Какое из наречий здесь уместно?

-Приведите свои примеры к каждому наречию.

Участвуют в работе, в беседе с учителем, отвечают на поставленные вопросы

-если сложить кол-во пятерок, четверок, троек и двоек, то получается 10.

-Нужно просто убрать 10

-Тройки

-Десять

-Одна

-на «удовлетворительно»

-Нет, нельзя

-Маловероятно

-приводят свои примеры

-На сколько частей разрезан торт?

-Сколько кусков с орешками?

-Ответьте на вопрос совы

-В каких ситуациях мы сталкиваемся с этими наречиями? Когда употребляем?

-С чем сегодня будем работать?

-Запишите тему урока

-на 12

-два

-да, прав

-в новостях, прогнозе погоды, ..в жизни

-с вероятностью

-записывают тему

Для тех, кто забыл, как разгадывать ребусы, напомню, что запятые рядом с рисунком сигналят о необходимости отбросить столько букв сколько нарисовано запятых (с той стороны, с которой они находятся по отношению к рисунку).

-Что же за слово здесь зашифровано?

(слово «Событие» ученики увидят после того, как разгадают ребус – эффект анимации по щелчку – появление)

-Что для вас означает событие?

-Какие события вы можете вспомнить?

-Только ли в личной жизни могут происходить события? Попробуйте привести примеры.

По ссылке на слайде переходим на Википедию, где рассказывается о событиях в разных сферах жизни

Разгадывают ребус

-событие

-…

-пошёл в школу, родился братик, выиграла наша команда….

-выбор президента, изобретение колеса или компьютера в своё время это тоже событие…

Запишем определение в тетрадь, приведем примеры событий (примеры учителя появляются по щелчку мыши).

Ребятам предлагается кубик и они выполняют его бросок, размышляя о событиях с применением наречий возможно, невозможно, маловероятно..

-Какие цифры могут выпасть на кубике?

-Есть ли среди них четные?

-Возможно ли событие выпало чётное число очков?

-Возможно ли событие выпало число очков, кратное 3

-Выпало более 4 очков

Записывают понятие в тетрадь

-1,2,3,4,5,6

-да, 2,4,6

-возможно

-да, 3,6

-может, таких чисел два – 5,6

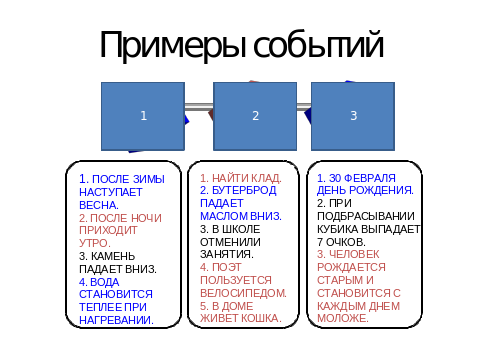
-Прочитайте примеры событий на этом слайде.

-На что Вы обратили внимание?

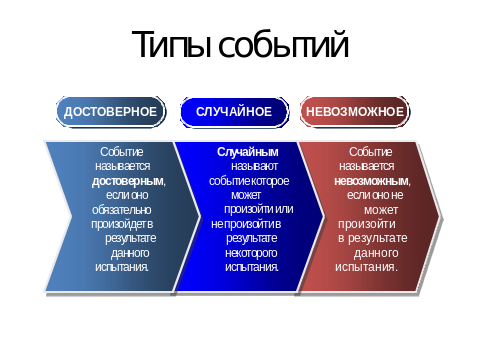
[на слайде после нажатия по щелчку на триггеры (с помощью эффекта анимации выход) открываются названия событий: достоверное, случайное, невозможное]

-Проверьте себя: правильно ли Вы сформулировали название событий

Ученики замечают, что есть события, которые никогда не происходят, всегда происходят или могут произойти, а могут не произойти, пробуют дать им название

-Проводят самоанализ

-Определите тип события.

-Париж – столица Франции

-За зимой наступит лето

-Во 2 триместре Коля получит по алгебре 4

-Приведите свои примеры

-достоверное

-невозможное

-случайное

-….

На следующих трех слайдах прочитайте вопрос.

-О каком событии идёт речь? Объясните свой ответ.

-Определяют к какому типу относится событие

-невозможное, потому что в феврале либо 28, либо 29 дней

С «ъ» знака слово начинаться не может, это невозможно

Ученику 9 класса может быть 14 лет, но не 14 месяцев – это год и 2 мес. (невозможно)

А вот событие с) случайное

Какие же примеры случайных экспериментов чаще всего изучают в математике?

Может быть, Вы уже сталкивались с такими задачами?

-После нашего урока, куда вы пойдёте?

-Расскажите, какие действия вы совершаете там?

-Иногда бывает, что в очереди кто-то кого-то может нечаянно толкнуть. Вот представим, что падают деньги. Какой вариант развития события возможен?

- в столовую

-стоим в очереди, заказываем еду, оплачиваем и идем за стол кушать

-монета упадет либо на одну, либо на другую сторону

-Да, это верно! Сегодня рассмотрим, какие ситуации возможны в этом опыте.

- но пока разгадайте ещё один ребус.

Как будете рассуждать?

Учитель в случае необходимости направляет ход рассуждения детей в нужное русло, по щелчку мыши открывает правильный вариант ответа – исход.

-Как Вы понимаете это слово?

Ученики отмечают, что наличие записи м.род даёт подсказку, что картинка расшифровывается как лис, е2-е4 ход в шахматах, слово, зашифрованное в ребусе – исход

-пробуют сформулировать, предлагают разные варианты

-Запишите определение в тетрадь

-пишут

-Итак, сколько же исходов при подбрасывании монеты?

-два

-Верно

Задолго до нашего рождения люди решали задачи, связанные с вероятностью, попробуем и мы с Вами

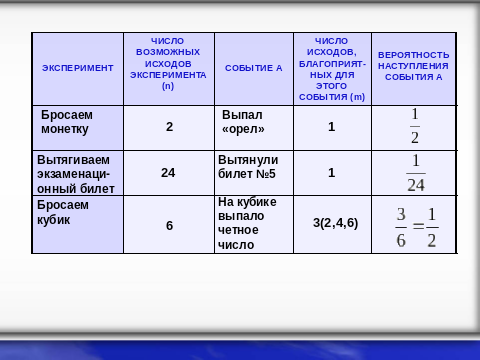
Анимация слайда настроена на вылет нужного объекта по управлению учителя (по щелчку левой кнопкой мыши).

Проведем эксперимент – бросаем монетку, событие – выпал орел.

-Сколько всего возможных исходов эксперимента?

-Чему равно число благоприятных исходов для этого события?

-Как Вам кажется, какова вероятность наступления события А?

(Если ученики затрудняются с правильным ответом, учитель помогает, подводит их к выводу формулы)

-Вытягиваем экзаменационный билет. Допустим, вытянули билет №5.

-Чему равно число исходов, благоприятных этому событию?

-Вы правы, допустим 24 возможных исхода, какова вероятность наступления события?

-Бросаем кубик, событие – на кубике выпало четное число. Насколько информативно это для вас?

-сколько таких вариантов?

-известно ли число возможных исходов эксперимента при бросании кубика?

-какова же вероятность наступления события?

-2

-1

В идеале кто-то отвечает ½

-1, не дожидаясь следующего вопроса учителя, ученики сообщают, что если для монеты известно о двух исходах, то в этом эксперименте нужно знать сколько билетов предлагалось на экзамен обучающимся.

-1/24

-значит, могли выпасть очки 2, 4 или 6

-3

-да, их 6

3/6=1/2

Итак, запишем формулу классической вероятности.

Составьте алгоритм решения простейших задач теории вероятностей.

Формулируют необходимые этапы алгоритма:

определить число всех возможных исходов
выяснить сколько благоприятных исходов
записать верную дробь

Прочтите условие

Каково число элементарных событий?

Чему равно число благоприятных исходов?

Найдите вероятность того, что игру будет начинать Петя.

Переведите обыкновенную дробь в десятичную

Вася, Петя, Коля и Леша бросили жребий – кому начинать игру. Найдите вероятность того, что игру будет начинать Петя.

0,25

Прочтите первое предложение задачи.

Вспомните алгоритм решения задач с помощью формулы классической вероятности.

Насколько информативно данное предложение задачи?

-Теперь дочитайте условие задачи.

-Какие сведения для нас важны здесь?

-Дайте ответ к этой задаче

Дежурные по классу Алексей, Иван, Татьяна и Ольга бросают жребий - кому стирать с доски. –Понятно, что число всех исходов (в данной задаче дежурных учеников) 4

-Найдите вероятность того, что стирать с доски достанется одной из девочек.

-что берем кол-во девочек – 2

-2/4=1/2=0,5

Примените составленный алгоритм к этой задаче.

-всего чисел 10

-делятся на три: 12,15,18 – 3

-вероятность 3/10 = 0,3

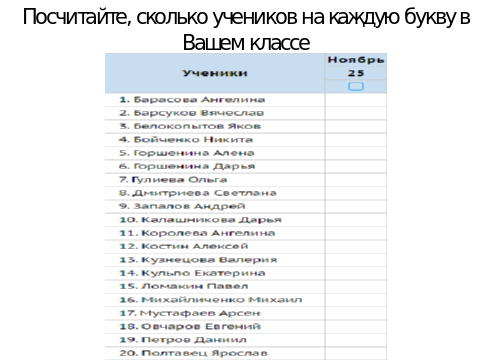
Посчитайте, сколько учеников в вашем классе на каждую букву

Сколько всего учеников в классе?

Б – 4

Г – 3

Д – 1

З – 1

К – 5

Л – 1

М – 2

О – 1

П – 2

Итак, получаем задачу

В Вашем классе 20 учеников.

На букву «Б» начинается 4 фамилии, на букву «Г» ‒ 3, на "Д" ‒ 1, на «З» – 1, на "К" ‒ 5, на «Л» – 1, на "М" ‒ 2, на "О" ‒ 1, на «П» ‒ 2.

а) Какова вероятность, что вызовут к доске ученика на букву "О"?

- Какие ещё вопросы Вы можете составить к этой задаче?

-Можно ли составить обратную задачу?

б) Известно, что вероятность ответа у доски некоторого ученика в классе равна 0,15. Может ли этим учеником быть Мустафаев? Гулиева?

1/20=0,05

-……

-М – 2, следовательно, вероятность 2/20=0,1, а у нас в условии 0,15, значит, нет, не может

-Г – 3, следовательно, вероятность 3/20 = 0,15, значит да, может.

Прочитайте условие задачи.

-Насколько информативно для вас первое предложение?

-Известно, что вероятность отгадать задуманное число 0,4. Какую информацию несет нам это предложение?

-Какими далее должны быть наши размышления для получения ответа на вопрос задачи?

-Как мы должны это делать?

-Делаем вывод

Написаны числа: 12, 14, 22, 23, 24, 27, 32, 35, 38, 42. Вася задумал одно из них. Известно, что вероятность отгадать задуманное число 0,4. Какое(ие) число(а) мог загадать Вася?

- чисел 10

-0,4=4/10, благоприятных исходов 4

-найти эти 4 благоприятных исхода

-определим, сколько раз повторяется каждая цифра

«1» - 2

«2» - 8

«3» - 4

«4» - 3

«5» - 1

«7» - 1

«8» - 1

-загаданное Васей число должно содержать цифру 3 – 23,32,35,38

Сменить деятельность, обеспечить эмоциональную разгрузку учащихся.

Раз – поднялись потянулись,

Два – согнулись, разогнулись,

Три в ладоши три хлопка,

На четыре – три кивка,

Пять руками помахать,

Шесть – тихонько сесть

Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу.

Вернемся к опыту с монетой. Исходов при бросании монеты вы сказали будет….

А как изменится ситуация если монету подбросить дважды?

Давайте свои рассуждения оформим в виде таблицы

Два – орел и решка

-дети рассуждают

-оформляют

Итак, при подбрасывании монеты исходов будет….

Тогда и задач для данного случая можно придумать больше чем при подбрасывании одной монеты. Рассмотрим одну из них.

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Вспоминаем алгоритм решения.

Что необходимо извлечь из условия?

-слушаю, продолжайте

-Какие ещё можно было бы здесь задать вопросы?

-Можно ли составить обратную задачу? [Учитель слушает ответы учеников, корректирует их размышления в случае необходимости]

-конечное число исходов - 4, благоприятное число исходов-2

-осталось подставить в формулу и записать ответ – 2/4=1/2=0,5

-……

В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадет ОРЕЛ, во второй - РЕШКА)

Примените изученный алгоритм, сообщите ответ

Ученики в таблице ищут указанный вариант ОР,

¼=0,25

Мы рассмотрели с вами задачи со случайным экспериментом при подбрасывании монет. Какие варианты были рассмотрены?

Можно ли изменить условие задачи?

Составьте таблицу, отражающую этот случай

Сформулируйте вопросы к этому случаю.

Попробуем найти закономерность количества строк таблицы от количества бросков монеты.

-Сколько строк в таблице при 1 броске монеты?

-Сколько строк в таблице при 2-х бросках монеты?

-Сколько строк в таблице при 3-х бросках монеты?

- 2, 4, 8 как связаны эти числа?

-Сформулируйте вывод

Эта формула нам нужна для самопроверки, чтобы мы не потеряли ни один из вариантов исходов.

В информатике вы будете работать с такой формулой при составлении таблиц истинности, только показатель степени там будет не количество бросков монеты, а количество переменных в логическом выражении.

-монету подбрасывали 1, 2 раза

-подбросим монету три раза

Заполняют таблицу

-………….

- 2 строки вариантов исходов + 1 строка заголовка

- 4 строки вариантов исходов + 1 строка заголовка

-8 строк вариантов исходов + 1 строка заголовка

-степень двойки

2¹ = 2

2² = 4

2³ = 8

-показатель степени – это количество бросков монеты, основание степени 2 – это количество всех исходов события (выпадает орел или решка)

Рефлексия

Что ты использовал сегодня на уроке?

Как ты действовал?

На что обратил внимание?

Допускал ли ты на уроке ошибки?

Как тебе кажется, чем вызвана твоя ошибка? На что ты не обратил внимание?

Что нужно сделать дома? [можно предложить задачу, в которой монету подбрасывают 4 раза]

-………

-…………

Резюме

В ходе данного урока был реализован системно-деятельностный подход: наличие мотивации на каждом этапе урока; система вопросов учителя, из которых большинство вопросы анализа и синтеза; вывод учащимися формулы классической вероятности; вывод формулы зависимости количества строк в таблице исходов бросков монеты от количества бросков; организация деятельности учащихся по составлению других вопросов к предложенным задачам, по составлению обратных задач.

Методическими особенностями данного урока являются:

оригинальная фабула урока;
визуализация на слайдах презентации, причем с помощью эффектов анимации на слайде постепенно открывается нужная информация, в сильном классе если ученики быстро дают ответ на вопрос задачи, учитель может по управляющей кнопке перейти сразу на следующий слайд, не тратя время на лишние для данных детей пояснения, и, наоборот, в слабом классе можно проговорить все этапы решения, прорабатывая сформулированный обучающимися алгоритм.
система задач, структуру которой можно представить следующим образом: задачи взяты из жизни, близкие и понятные детям, одна из задач составлена именно для данного класса (информацию можно использовать скриншотом с сетевого города);
задачи-перевертыши, суть которых заключается в том, чтобы учащиеся научились правильно работать с текстом, вдумчиво читать условие, анализировать сразу в момент чтения, оценивая информативность каждого предложения;
рефлексия организована системой вопросов таким образом, чтобы каждый ученик вспомнил именно свою работу на уроке.