Тема: Розв’язування задач і вправ підвищенної складності. Комбінаторика.
Мета: Активізувати пізнавальну діяльність учнів, формування вміння міркувати, аналізувати і робити висновки, розвивати творчі здібності та логічне мислення учнів.
Хід уроків
І. Організаційний момент
ІІ. Вивчення нового матеріалу. Розв’язування вправ на осмислення нового матеріалу.
Вступне слово. Сьогодні я хочу познайомити вас з комбінаторними задачами. Комбінаторика – це розділ математики, в якому вивчається питання про те, скільки різних комбінацій можна скласти. Зараз я назву основні методи розв’язування комбінаторних задач. Це перебір числа елементів певної множини та укладання різноманітних комбінацій (з повтореннями й без повторень) із 2-3 елементів.
Задача 1. Жителі планети «Кін-дза-дза» обходилися для всіх випадків одним словом «ку». А якби алфавіт у них складався з двох літер К і У, то скільки слів було б у них в словнику, за умови, що букви в слові можуть повтор.ватися і слова складаються тільки з двох букв?
Вчитель показує рішення на дошці:
Із букв К і У можна скласти такі слова: ку, кк, уу, ук.
Задача 2. У жителів планети АХО в алфавіті 3 букви: А,О,Хю Слова в мові складаються з трьох букв. Яка найбільша кількість слів може бути в словнику жителів цієї планети? (Букви в словах повторюватись не повинні)
Розв’язує учитель коло дошки: аох, ахо, оах, оха, хао, хоа.
Висновок: в цих задачах нам довелося перебирати всі можливі варіанти, або, як зазвичай кажуть у таких випадках – всі можливі комбінації. Тому подібні завдання називають комбінаторними.
Розглянемо ще одну задачу.
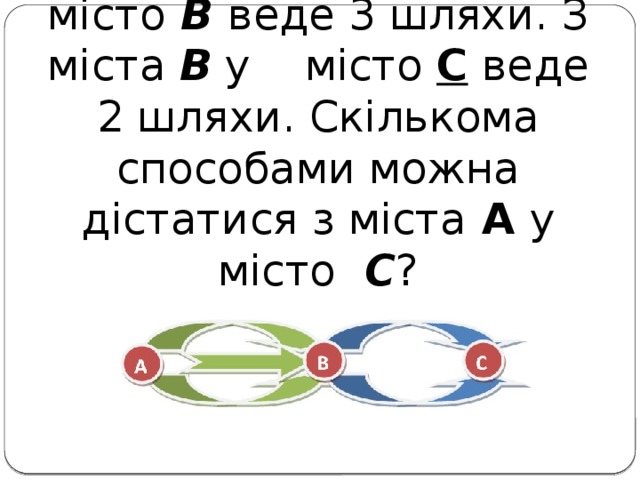
Задача 3. З міста А у місто В веде 3 шляхи. З міста В у місто С веде 2 шляхи. Скількома способами можна дістатися з міста А у місто С.
Розв’язавши цю задачу ми довели основне правило комбінаторики:
Нехай є дві дії. Причому першу дію можна виконати n способами, а другу дію можна виконати m способами, тоді послідовність дій: спочатку першої, а потім другої можна виконати n•m способами.
Шляхів із А в В: 3
=> із А в С: 3•2=6
Шляхів із В в С: 2
Відповідь: 6 шляхів
Задача 4. НА вершину гори веде 7 стежок. Скількома способами турист може піднятися і спуститися з гори? (7•7=49)
Якщо різними шляхами? (7•6=42)
Слово вчителя: Виявляється комбінаторні завдання можуть нам зустрітися в будь-якому предметі. Наприклад в літературі. Візьмемо твір російського письменника, байкаря Івана Андрійовича Крилова – «Квартет»
Перекладач: Ф. Скляр
Вигадниця Мартишка,
Осел,
Козел
Та клишоногий Мішка
Затіяли Квартет Зіграть.
Дві скрипки, ноти, бас і альт дістали
Й під липу в лузі посідали,
Щоб світ мистецтвом чарувать.
Ударили в смички, - ладу ж дарма шукать!
«Стій, братця, стій! - кричить їм
Мавпа, - постривайте!
Хіба заграєм так? Інакше посідайте.
Ти з басом, Мишенько, сідай проти альта,
Я, прима, сяду проти втори;
Тоді вже піде музика не та:
У танець підуть ліс і гори!»
Знов сіли, почали Квартет;
….. і далі
Задача 5.Назвіть учасників квартету (козел, осел, мартишка, мішка)
Скільки існує різних способів посадити цих персонажів?
Цю задачу розв’язати можна за допомогою правила множення: Кількість способів якими ми можемо заповнити 1 позицію доповнює максимальній кількості способів n, 2 позицію n-1 (оскільки перший елемент вже займає одне місце); останню – одним способом. Згідно основному правилу комбінаторики перемножуємо:
Р= n(n-1)х…х1
Давайте обміркуємо задачу про квартет. Мішка може сісти на одне з 4х місць, Козел може сісти на одне з 3х місць, Осел може сісти на одне з 2х місць, Мартишка може сісти на 1 місце, що залишилось.
Тобто: 4х3х2х1=24 варіанта
ФІЗКУЛЬТХВИЛИНКА
Резервні задачі:
Задача 1. Скільки двозначних чисел можна скласти, використавши цифри 1,7,4 (цифри можуть повторюватись)
3х3=9
(на перше місце цифру можна обрати трьома способами, після чого на друге місце теж цифру можна обрати трьома способами)
11,14,17,41,44,47,71,74,77
Задача 2. Скільки двозначних чисел можна скласти з цифр 9, 7,0 (цифри можуть повторюватись)?
2х3=6
(нуль не може стояти на першій позиції)
99,97,90,79,77,70
Задача 3. У класі 25 учнів, скількома способами можна обрати командира класу та його заступника?
25х24=600
Задача 4. У розіграші першості країни з футболу бере участь 16 команд. Скількома способами можуть бути розподілені золота і срібна медалі?
16х15=240
ІІІ. Підсумок уроку