Работа проводится после изучения темы "Многограники". В первой части - задачи с выбором ответов. Задачи второй и третьей части предлагаются наиболее подготовленным учащимся.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Итоговое тестирование по теме "Многогранники"
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Итоговое тестирование по теме "Многогранники"»
Полезное для учителя
Распродажа видеоуроков!
2230 руб.
3190 руб.
1740 руб.
2480 руб.
2000 руб.
2860 руб.
1790 руб.
2560 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
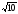 м; г)
м; г) 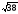 м; д)
м; д) 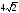 м.
м.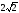
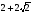 ; б)
; б) 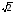 ; в) 2; г)
; в) 2; г) 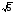 ; д)
; д) 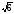 .
.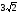 см; б) 3см,
см; б) 3см, 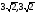 см; в)
см; в) 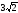 см,
см, 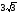 см.
см.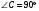 ,
, 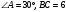 см. Боковые ребра наклонены к основанию под углом 600. Найдите высоту пирамиды.
см. Боковые ребра наклонены к основанию под углом 600. Найдите высоту пирамиды.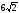 см. Через сторону AB и вершину C1 проведено сечение. Найдите угол между плоскостью сечения и плоскостью основания, если длина бокового ребра равна 3 см.
см. Через сторону AB и вершину C1 проведено сечение. Найдите угол между плоскостью сечения и плоскостью основания, если длина бокового ребра равна 3 см.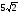 м; б)
м; б) 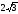 м; в) 50м; г) 12м; д)
м; в) 50м; г) 12м; д) 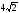 м.
м.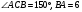 см. Боковы ребра наклонены к основанию под углом 450. Найдите высоту пирамиды.
см. Боковы ребра наклонены к основанию под углом 450. Найдите высоту пирамиды.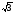 см и углом при вершине 300. Диагональ наименьшей боковой грани образует с плоскостью основания призмы угол 450. Найдите площадь полной поверхности призмы.
см и углом при вершине 300. Диагональ наименьшей боковой грани образует с плоскостью основания призмы угол 450. Найдите площадь полной поверхности призмы.















