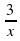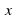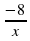Тема: « Графическое решение уравнений». (слайд №1)
Цели: (слайд №2)
Повторить ранее изученные графики функций; рассмотреть графический способ решения уравнений.
Усиление роли графических представлений при формировании основных понятий темы, увеличение удельного веса знаний, предлагающих работу с графиками функций.
Решение задач по теме с использованием ИКТ; формирование и развитие познавательной мотивации учащихся к получению новых знаний; способствовать выработке навыков и умений построения графиков функций.
Структура урока: (слайд №3)
Актуализация опорных знаний учащихся.
Постановка учебной задачи.
Изучение нового материала.
Закрепление изученного материала.
Подведение итогов учебной деятельности, домашнее задание.
Ход урока.
Актуализация опорных знаний. Устный опрос (слайд №4)
Что такое функция?
Что называется графиком функции?
Что является графиком функции:
а) y=kx + b; б) y=kx; в) y=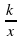 ; г) y=x3; д) y= x2
; г) y=x3; д) y= x2
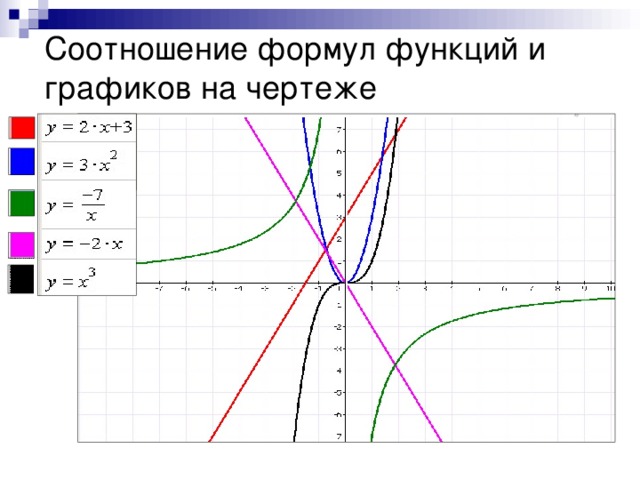
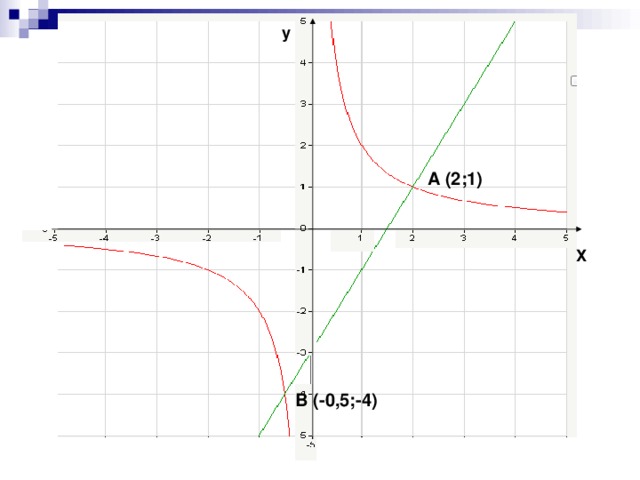
4) Соотнесите формулы функций и графики на чертеже (слайд №5)
а) y= 2x+3; б) y= 3x2; в) y = -2x; г) y= x3; д) y=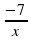 ;
;
2. Постановка учебной задачи. Изучение нового материала.
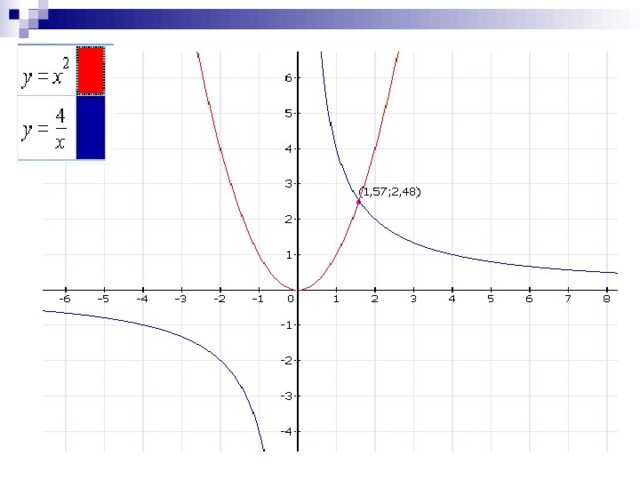
Рассмотрим уравнение x2 = 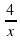 , способ решения которого нам неизвестен. Однако с помощью графиков можно найти приближенные значения корней этого уравнения.
, способ решения которого нам неизвестен. Однако с помощью графиков можно найти приближенные значения корней этого уравнения.
1)Рассмотрим теорию этого вопроса: (слайд №6)
Чтобы решить уравнение f (x) = q (x), где f (x) и q (x) – некоторые выражения с переменной x, нужно в одной и той же системе координат построить графики функций y= f(x) и y= q(x) и найти абсциссы точек пересечения этих графиков. Найденные числа будут корнями данного уравнения.
2)Введём алгоритм графического решения уравнения вида f(x) = q(x).
Алгоритм графического решения уравнений (слайд №7)
Чтобы графически решить уравнение f(x) = q(x), надо:
рассмотреть две функции y= f(x) и y=q(x);
построить график функции y=f(x);
построить график функции y=q(x);
найти точки пересечения построенных графиков; абсциссы этих точек – корни уравнения f(x)=q(x).
3)Итак, решим уравнение x2 = 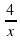 графическим способом.
графическим способом.
y=x2 –парабола x 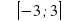 шаг 0,5
шаг 0,5
| x | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | 9 | 6,25 | 4 | 2,25 | 1 | 0,25 | 0 | 0,25 | 1 | 2,25 | 4 | 6,25 | 9 |
| x | 0,5 | 1 | 2 | 4 | 8 |
| y | 8 | 4 | 2 | 1 | 0,5 |
| x | -0,5 | -1 | -2 | -4 | -8 |
| y | -8 | -4 | -2 | -1 | -0,5 |
Чертёж на слайде №8.
А(1,57; 2,48) –точка пересечения. Абсцисса этой точки равна 1,57. Значит x=1,57- решение уравнения x2 = 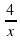 .
.
Ответ: x=1,57
Вывод: на практике из обилия способов выбирают тот, который больше нравится или более понятен. Графические способы решения уравнений понятны, но они не дают стопроцентной гарантии решения любого уравнения. Это надо учитывать. Возможен вариант, что корень уравнения – это дробное или иррациональное число, т. е. мы сможем найти только приближённое значение корня. Либо уравнение таково, что ограниченные размеры листа не позволяют построить график.
3.Закрепление изученного материала. (слайд №9)
1. Запишите функции, по которым будут строиться графики для решения уравнений
а) x2=6-x;
б) x2= 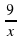 ;
;
в) 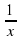 =2x+1;
=2x+1;
г) 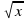 = x- 6
= x- 6
2. Решаем в тетрадях уравнение 2x-3- 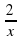 =0 , используя алгоритм. (слайд №10)
=0 , используя алгоритм. (слайд №10)
| x | -0,5 | -1 | -2 | -4 |
| y | -4 | -2 | -1 | -0,5 |
Ученики в тетрадях самостоятельно строят графики и находят точки пересечения, выписывают корни уравнения. После проверки работы учеников на местах, учитель демонстрирует результат построения графиков на слайде №11.
3.Решаем графически уравнение в тетрадях и на доске (слайд №12)
2x2 – 3x- 2=0
(один из учеников решает за обратной доской это уравнение с помощью формул)
2x2-3x-2=0
D=b2-4ac=9+16=25, 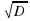 =
=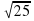 =5
=5
x1, 2=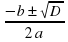
x1=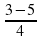 =-0,5; x2=
=-0,5; x2=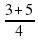 =2.
=2.
Ответ: -0,5; 2.
При решении этого уравнения проще было воспользоваться уже известным нам способом решения квадратного уравнения с помощью формул.
Вывод: на практике из обилия способов выбирают тот, который более рационален. Если решить необходимо именно графическим методом, то выбирают более простой в построении способ. Графические способы решения уравнений понятны, но чаще всего они не дают гарантии решения любого уравнения.
4.Итог урока. Домашнее задание.( Подводят итоги ученики)
Что нового вы узнали на уроке? Достигнуты ли цели урока? (можно использовать слайд №13)
5.Дополнительное задание (при наличии времени).(слайд №14)
Сколько корней имеет уравнение
x2=-5x+3
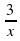 =
=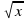
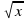 =-x2
=-x2
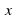 =
=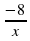
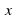 3=-x
3=-x
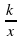 ; г)
; г) 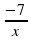 ;
;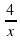 , способ решения которого нам неизвестен. Однако с помощью графиков можно найти приближенные значения корней этого уравнения.
, способ решения которого нам неизвестен. Однако с помощью графиков можно найти приближенные значения корней этого уравнения.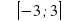 шаг 0,5
шаг 0,5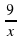 ;
;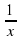 =2
=2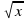 =
= 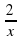 =0 , используя алгоритм. (слайд №10)
=0 , используя алгоритм. (слайд №10)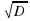
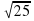 =5
=5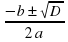
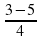 =-0,5;
=-0,5; 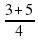 =2.
=2.