Игра. Аукцион. Графическое решение уравнений и систем второй степени. 9 класс.
Оборудование: координатная доска, магнитная доска, графопроектор,
аукционный молоточек, карточки с заданиями, 2 конверта «Сюрприз», плакат с правилами игры.
Правила игры. Класс делится на 3,4 команды. Выбирается жюри. Все команды
получают в банке (у ведущего) первоначальный капитал 100 игровых рублей под 30% т.е.
в конце игры вернуть в банк 130 игровых рублей. Капитанам команд выдаются
номера (1,2,3,4).Стартовая цена 10 руб. Торговый шаг 5 руб. Каждая команда заполняет
лицевой счет в течение игры. Вознаграждение за правильный ответ от 50 до 100 руб.
в зависимости от сложности вопроса. Если команда неправильно ответила на вопрос,
штраф в банк 10 руб., а лот снимается с торгов и выставляется в конце игры для повторной продажи.
Лицевой счет. № Команды____________
Получено в банке_________
№ записи
Приход
Расход
Остаток
1
100 руб.
---- -------
100 руб.
2
-------
35 руб.
65 руб.
3
50 руб.
---------
105 руб.
и т. д.
1 ТУР.
Открытый лот.
Конкретный вопрос.
Является ли пара чисел (8;5) решением системы?
х2 -у2 =39 Стартовая цена 10 руб. Вознаграждение 50 руб.
ху+6х=88 Ответ: является.
Какие из графиков функций расположены ниже оси Х?
1) у=- х3 Стартовая цена 10 руб. Вознаграждение 50 руб.
2) у=- |3/х|
3) у=(х-1)2 +3
4) у=-√ х
5) у=- (х+4)2 -3
6) у=| х +3|
7) (х-5)2 +(у-7)2 =1 Ответ:{ 2;4;5.}
3. Какие из графиков функций предыдущего задания расположены выше оси Х?
Стартовая цена 10 руб. Вознаграждение 50 руб.
Ответ: {3;6;7.}
Вознаграждение 50 руб.
Ответ: 2 решения.
у=-| х| +4
2
Вознаграждение 60 руб. Ответ: 2 решения.
6. Сколько решений имеет система уравнений?
2 +у2 =25 Вознаграждение 70 руб.
у=-х2 +5 Ответ: 3 решения.
7. Сколько решений имеет система уравнений?
х=у2 Ответ: 1 решение.
8. Решите уравнение: 2/х-х2 +3=0
Вознаграждение 80 руб.
Ответ: х1 =-1 х2 =2.
9. Решите систему уравнений:
х2 +у2 =16 Ответ: (4;0), (0;4), (-4;0), (0;-4).
10. Разыгрывается лот «Сюрприз».
Стартовая цена 10 руб.
Команда, купившая этот лот, получает в конверте карточку, в которой написано:
Вы имеете право на приобретение по начальной стартовой цене одного из лотов
2 тура аукциона или получить в банке премию в размере 50 руб.
11. Решите систему уравнений:
у=-(х+2)2 +4 Ответ: (-3;3), (0;0).
12. Решить уравнение
4/х-х2 +2=0 Вознаграждение 70 руб.
Ответ: х=2
2 ТУР.
Закрытый лот.
Неизвестный вопрос.
Ведущий игры объясняет правила игры во втором туре.
1. Дана незаконченная система уравнений.
Дополните систему такой функцией, чтобы она имела 2 решения.
3
Вознаграждение 90 руб.
2. Сколько решений имеет система?
х2 +у2 =16 Ответ: 4 решения.
3. Доказать, что графиком функции является окружность х2 +у2 +4х-2у+1=0
Вознаграждение 90 руб.
Ответ: х2 +4х+4+у2 -2у+1-4=0
(х+2)2 +(у-1)2 =4
4. Разыгрывается лот №4 «Сюрприз».
Стартовая цена 10 руб.
Команда, купившая этот лот, получает в конверте карточку, в которой написано:
Вы совершили удачную сделку, ваши наличные удваиваются!
х2 +у2 -6х+8у=0 Вознаграждение 100 руб.
у=- х+4 Ответ: (3;1), (8;- 4).
6. При каких значениях параметра а уравнение | х2 -2х-3|=а имеет 3 корня?
Вознаграждение 100 руб.
Ответ: а=4
7. При каких значениях параметра а уравнение –| х2 -8х+12| =а имеет 4 корня?
Вознаграждение 100 руб.
Ответ: при а є (-4;0)
у=-| х| +2
Дополните эту систему такой функцией, чтобы она имела 3 решения.
Вознаграждение 1000 руб.
3 ТУР.
Повторный лот.
В этом туре выставляется лот, который не решили в предыдущих турах.
7
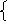
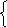 ху=8
ху=8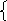 5. Сколько решений имеет система уравнений? у=х2
5. Сколько решений имеет система уравнений? у=х2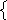 х2+у2=25 Вознаграждение 70 руб.
х2+у2=25 Вознаграждение 70 руб.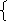 у=-| 4/х| Вознаграждение 80 руб.
у=-| 4/х| Вознаграждение 80 руб.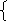 у= |3/х| Вознаграждение 70 руб.
у= |3/х| Вознаграждение 70 руб.















