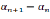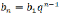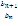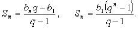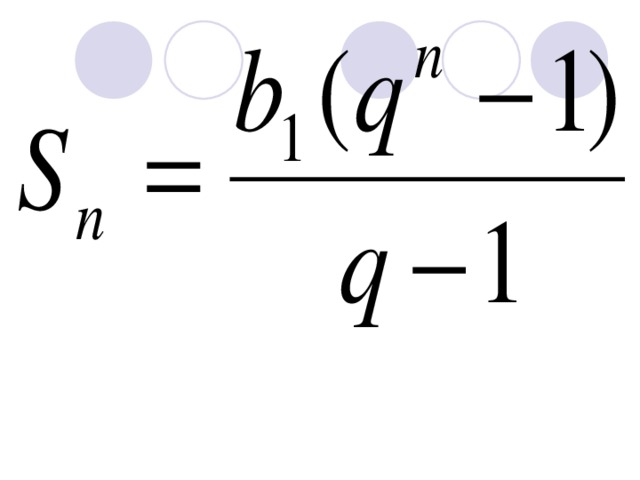Тема урока «Сумма n первых членов геометрической прогрессии»
Цели урока:
1. Образовательная: познакомиться с формулой суммы n первых членов геометрической прогрессии, учиться применять на практике.
1. Воспитательная: учить слушать и слышать, уважать чужое мнение, поддерживать других и быть к ним благожелательными.
2. Развивающие: способствовать развитию критического мышления через восприятие информационного текста; используя приемы технологии критического мышления, стимулирующие мыслительную и творческую деятельность учеников, учить вдумчивому чтению.
Ход урока
I. Орг. момент.
- Здравствуйте, садитесь.
II. Стадия вызова.
Сегодня, ребята, мы продолжаем изучение геометрической прогрессии. Давайте вместе с вами вместе попытаемся сформулировать тему нашего урока.
Слайд 1
вспомним алгоритм изучения темы арифметическая прогрессия.
Работа в тетради, на доске число. Запишем тему урока в тетради: «Сумма n первых членов геометрической прогрессии. Мы должны познакомиться с формулой суммы первых п членов геометрической прогрессии и учиться применять ее Слайд 2
Прежде чем перейти к новой темы, мы с вами продолжаем готовиться к итоговой аттестации. Слайд 3
Работа с сигнальными карточками
У каждой группы на столе находятся карточки с формулами. Учитель называет формулу, дети, молча, поднимают карточку.
+(n-1)d
Учитель:
•??? обозначение разности арифметической прогрессии
Сейчас вашему вниманию будут представлены слайды с записью членов последовательностей. Вам необходимо определить ее вид и ответить на поставленные вопросы Слайд 4
Итак, мы повторили основные формулы геометрической прогрессии. Вы показали свои знания по предыдущим темам. Скажите, кто из вас играет в шахматы? Представьте себе шахматную доску...
Слайд 5
По преданию, шахматы были изобретены в V веке нашей эры в Индии. Индийский царь Шерам, впервые познакомившись с шахматами, восхитился их своеобразием и обилием красивых комбинаций. Узнав, что замечательную игру изобрёл его подданный Сета, царь призвал к себе мудреца, желая лично наградить за выдумку-Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -сказал царь.
Мудрец поклонился.
Слайд 6
Слайд 7
Масса такого числа зерен больше триллиона тонн.
Индусский царь не в состоянии был выдать подобной награды.
Но будь он силен в математике, он бы не попал впросак…
Слайд 8
18 квинтиллионов 446 квадриллионов
744 триллиона 73 миллиарда
709 миллионов 551 тысяча 615 зерен Слайд 9 ВЫВОД
Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, - но что награда, о которой говорит предание, должна была выразиться именно таким числом в этом ты сам можешь убедиться.
Фактически, число зерен, о которых идет речь, является суммой 64 членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
S = 1+2+22+23+24+…….+262+263 Слайд 10
III. Осмысление.
Как выведена и применяется формула для решения подобных задач вам и предстоит выяснить. Откройте учебники на странице 160.
Слайд 11
Мы выяснили, что сумма n первых членов геометрической прогрессии может быть найдена по формулам:
запишем их в тетрадь.
Слайд 12
Слайд 13 первичная проверка знаний
IV. Рефлексия.
Вернемся к поставленным в начале урока целям. Чего мы достигли?
Слайд 15
Домашнее задание
Просмотр содержимого документа
«конспект»
Тема урока «Сумма n первых членов геометрической прогрессии»
Цели урока:
1. Образовательная: познакомиться с формулой суммы n первых членов геометрической прогрессии, учиться применять на практике.
Воспитательная: учить слушать и слышать, уважать чужое мнение, поддерживать других и быть к ним благожелательными.
Развивающие: способствовать развитию критического мышления через восприятие информационного текста; используя приемы технологии критического мышления, стимулирующие мыслительную и творческую деятельность учеников, учить вдумчивому чтению.
Ход урока
I. Орг. момент.
- Здравствуйте, садитесь.
II. Стадия вызова.
Сегодня, ребята, мы продолжаем изучение геометрической прогрессии. Давайте вместе с вами вместе попытаемся сформулировать тему нашего урока.
Слайд 1
вспомним алгоритм изучения темы арифметическая прогрессия.
Работа в тетради, на доске число. Запишем тему урока в тетради: «Сумма n первых членов геометрической прогрессии. Мы должны познакомиться с формулой суммы первых п членов геометрической прогрессии и учиться применять ее Слайд 2
Прежде чем перейти к новой темы, мы с вами продолжаем готовиться к итоговой аттестации. Слайд 3
Работа с сигнальными карточками
У каждой группы на столе находятся карточки с формулами. Учитель называет формулу, дети, молча, поднимают карточку.
Учитель:
обозначение разности арифметической прогрессии
Сейчас вашему вниманию будут представлены слайды с записью членов последовательностей. Вам необходимо определить ее вид и ответить на поставленные вопросы Слайд 4
Итак, мы повторили основные формулы геометрической прогрессии. Вы показали свои знания по предыдущим темам. Скажите, кто из вас играет в шахматы? Представьте себе шахматную доску...
Слайд 5
По преданию, шахматы были изобретены в V веке нашей эры в Индии. Индийский царь Шерам, впервые познакомившись с шахматами, восхитился их своеобразием и обилием красивых комбинаций. Узнав, что замечательную игру изобрёл его подданный Сета, царь призвал к себе мудреца, желая лично наградить за выдумку-Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал, -сказал царь.
Мудрец поклонился.


Слайд 6

Слайд 7
Масса такого числа зерен больше триллиона тонн.
Индусский царь не в состоянии был выдать подобной награды.
Но будь он силен в математике, он бы не попал впросак…
Слайд 8
18 квинтиллионов 446 квадриллионов
744 триллиона 73 миллиарда
709 миллионов 551 тысяча 615 зерен Слайд 9 ВЫВОД
Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, - но что награда, о которой говорит предание, должна была выразиться именно таким числом в этом ты сам можешь убедиться.
Фактически, число зерен, о которых идет речь, является суммой 64 членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
S = 1+2+22+23+24+…….+262+263 Слайд 10
III. Осмысление.
Как выведена и применяется формула для решения подобных задач вам и предстоит выяснить. Откройте учебники на странице 160.
Слайд 11
Мы выяснили, что сумма n первых членов геометрической прогрессии может быть найдена по формулам:
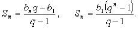
запишем их в тетрадь.
Слайд 12
Слайд 13 первичная проверка знаний
IV. Рефлексия.
Вернемся к поставленным в начале урока целям. Чего мы достигли?
Слайд 15
Домашнее задание
Просмотр содержимого презентации
«формула суммы геометрической пр»

ПРОГРЕССИИ
АРИФМЕТИЧЕСКАЯ
ГЕОМЕТРИЧЕСКАЯ
1. Определение
1. Определение
2.Формула n –го члена
2.Формула n –го члена
3. Формула суммы n первых членов.

Формула суммы
первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии
- Формула суммы первых n членов геометрической прогрессии

ПОВТОРЕНИЕ
1.Установить соответствие между графиками функций и формулами, которые их задают.
2.Устный счет.
3.Работа с сигнальными карточками.
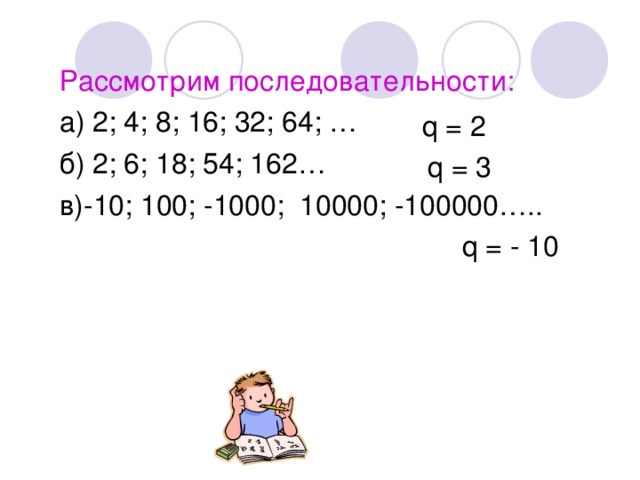
Рассмотрим последовательности:
а) 2; 4; 8; 16; 32; 64; …
б) 2; 6; 18; 54; 162…
в)-10; 100; -1000; 10000; -100000…..
q = - 10
q = 2
q = 3

Шахматная игра была придумана в Индии, и когда индусский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что она изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку. Изобретатель, его звали Сета, явился к трону повелителя.

- Почему так хитро улыбнулся Сета?
- Прав ли был индусский царь, считая просьбу Сеты ничтожной, полагая, что все зерна пшеницы уместятся в один мешок?

Пусть все пространство их будет сплошь засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду…
С изумлением внимал царь словам старца.
- Назови мне это чудовищное число,- сказал он в раздумьи.

18 446 744 073 709 551 615
-Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три миллиарда семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

Вывод
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая моря, и океаны, и горы, и пустыню, и Арктику с Антарктикой, и получить удовлетворительный урожай, то, пожалуй, лет за 5 он смог бы рассчитаться.
Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до настоящего времени.
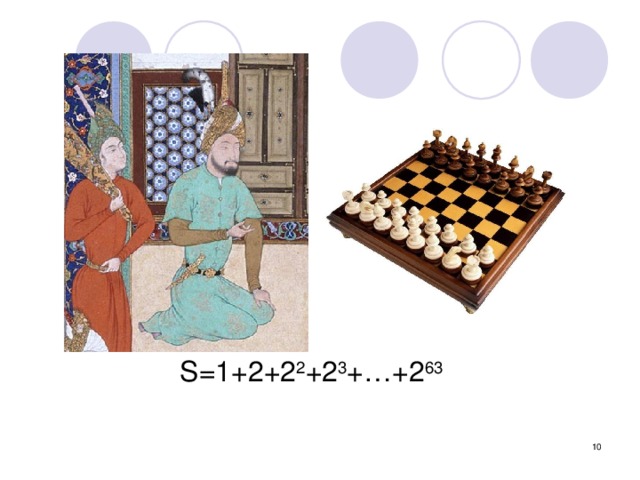
S=1+2+2 2 +2 3 +…+2 63

Сумма n первых членов геометрической прогрессии.
S n = b 1 + b 2 + b 3 + … + b n
S n = b 1 + b 1 q + b 1 q 2 + … + b 1 q n-1
Умножим обе части равенства на q.
S n q = b 1 q+b 1 q 2 +b 1 q 3 + … + b 1 q n-1 + b 1 q n
Вычтем из второго равенства первое.
S n q – S n = b 1 q n - b 1
S n (q – 1) = b 1 (q n - 1)
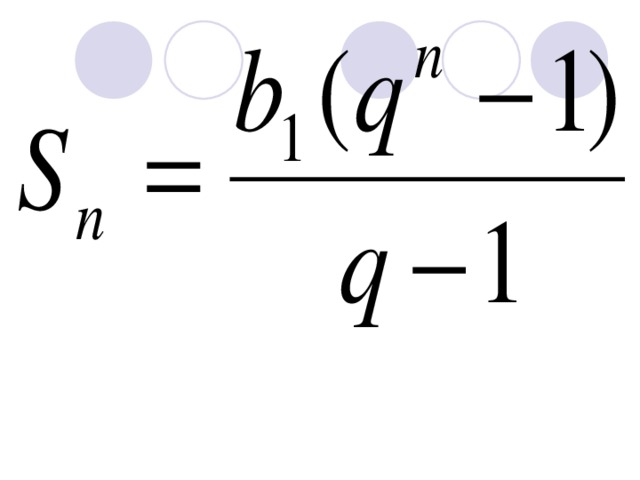

Закрепление
1. № 648(а)
2. № 649(а)

Самостоятельная работа
Домашнее задание
- С ОСТАВИТЬ КРОССВОРД ПО ТЕМЕ
- ПРОГРЕССИИ.

Спасибо!
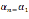 +(n-1)d
+(n-1)d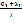 n
n