Тесты для диагностического контроля по алгебре
(8 класс)
Составила учитель математики МБОУ Большемурашкинская СОШ Житнякова О.С
Критерии оценивания работы:
5-7 заданий базового уровня – «3»,
8-10 заданий – «4»,
11-12 заданий – «5».
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 5х2 -3х+2 = 0 равен
1)19; 2)-1; 3) 49; 4)-31.
А 2. При каком условии полное квадратное уравнение не имеет корней.
1) D=0 2) D>0 3) D<0
А 3. Координаты вершины параболы, заданной уравнением у = - х2 +6х, равны
1) (6;0) 2) (-3;-9) 3) (3;9) 4) (0;0)
А 4.Сумма корней уравнения равна
1) 3; 2) -3; 3) 7; 4) -7.
А5. Найдите наименьшее значение функции у = х2 – 4х + 5.
1) 1; 2)-1; 3) 5; 4) – 4.
А 6. Решите уравнение 0,5у2 = 8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
А 7. Найдите b в уравнении x2+bx-12=0, если оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Часть В
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большого и меньшего корней уравнения х2+5х-24=0.
B2. Принадлежит ли графику функции у = х2 – 13х + 40 точка А (4;4)?
B3. Разложите на множители х2 – 10х+9.
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 7х2 +6х+1 = 0 равен
1)32; 2)2; 3) -64; 4) 8.
А 2. При каком условии полное квадратное уравнение имеет единственный корень.
1) D=0; 2) D>0; 3)D<0.
A3. Координаты вершины параболы, заданной уравнением у = - х2 - 4х +1, равны
1) (-2;5) 2) (2;-3) 3) (4;1) 4) (0;1)
А 4. Сумма корней уравнения равна
1) 3; 2) -3; 3) 8; 4) -8.
А 5. Найдите наибольшее значение функции у = -х2 + 4х - 5.
1) 1; 2)-5; 3) -1; 4) 4.
А 6. Решите уравнение а2=100
1) 5; 2) 20; 3) 5;-5 4) 20; -20
А 7. Найдите с в уравнении 2x+8x+c=0, если оно имеет корень 5.
1) 90; 2) -90; 3) 45; 4) -45.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большего и меньшего корней уравнения х2-9х+14=0.
B2. Принадлежит ли графику функции у = х2 – 11х + 24 точка А (2;6)?
B3. Разложите на множители х2 +10х+9.
Просмотр содержимого документа
«Тесты для диагностического контроля по алгебре (8 класс) »
Тесты для диагностического контроля по алгебре
(8 класс)
Составила учитель математики МБОУ Большемурашкинская СОШ Житнякова О.С
Критерии оценивания работы:
5-7 заданий базового уровня – «3»,
8-10 заданий – «4»,
11-12 заданий – «5».
Вариант 1
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 5х2 -3х+2 = 0 равен
1)19; 2)-1; 3) 49; 4)-31.
А 2. При каком условии полное квадратное уравнение не имеет корней.
1) D=0 2) D0 3) D
А 3. Координаты вершины параболы, заданной уравнением у = - х2 +6х, равны
1) (6;0) 2) (-3;-9) 3) (3;9) 4) (0;0)
А 4.Сумма корней уравнения 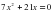 равна
равна
1) 3; 2) -3; 3) 7; 4) -7.
А5. Найдите наименьшее значение функции у = х2 – 4х + 5.
1) 1; 2)-1; 3) 5; 4) – 4.
А 6. Решите уравнение 0,5у2 = 8
1) 2;-2; 2) 2; 3) 4;-4; 4) 4;
А 7. Найдите b в уравнении x2+bx-12=0, если оно имеет корень 4.
1) 1; 2) -1; 3) 7; 4) -7.
Часть В
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большого и меньшего корней уравнения х2+5х-24=0.
B2. Принадлежит ли графику функции у = х2 – 13х + 40 точка А (4;4)?
B3. Разложите на множители х2 – 10х+9.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1.Решите систему уравнений 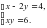
С 2. Сократите дробь .
Вариант 2
Часть А.
К каждому заданию этой части даны 4 варианта ответа, из которых только один верный. Запишите цифру, которая обозначает номер выбранного Вами ответа.
A1. Дискриминант уравнения 7х2 +6х+1 = 0 равен
1)32; 2)2; 3) -64; 4) 8.
А 2. При каком условии полное квадратное уравнение имеет единственный корень.
1) D=0; 2) D0; 3)D
A3. Координаты вершины параболы, заданной уравнением у = - х2 - 4х +1, равны
1) (-2;5) 2) (2;-3) 3) (4;1) 4) (0;1)
А 4. Сумма корней уравнения 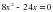 равна
равна
1) 3; 2) -3; 3) 8; 4) -8.
А 5. Найдите наибольшее значение функции у = -х2 + 4х - 5.
1) 1; 2)-5; 3) -1; 4) 4.
А 6. Решите уравнение 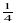 а2=100
а2=100
1) 5; 2) 20; 3) 5;-5 4) 20; -20
А 7. Найдите с в уравнении 2x +8x+c=0, если оно имеет корень 5.
+8x+c=0, если оно имеет корень 5.
1) 90; 2) -90; 3) 45; 4) -45.
Часть В.
К каждому заданию этой части записать краткий ответ.
B1. Найдите разность большего и меньшего корней уравнения х2-9х+14=0.
B2. Принадлежит ли графику функции у = х2 – 11х + 24 точка А (2;6)?
B3. Разложите на множители х2 +10х+9.
Часть С.
Подробные и обоснованные решения заданий этой части напишите аккуратно и разборчиво на листе.
С 1. Решите систему уравнений 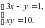
С 2. Сократите дробь  .
.
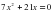 равна
равна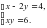
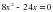 равна
равна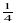 а2=100
а2=100  +8x+c=0, если оно имеет корень 5.
+8x+c=0, если оно имеет корень 5. 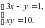
 .
.















