Одним из существенных моментов в организации обучения, как известно, является контроль за знаниями или умениями учащихся. Контроль должен выявить, владеют ли учащиеся фактическим материалом, умеют ли применить свои знания в различных ситуациях, могут ли сравнивать, обобщать конкретные факты, делать общие заключения. Без получения такой информации, без обратной связи говорить об управляемом учебном процессе не приходится. Существует много методов педагогической диагностики. Наблюдение, опрос, анкетирование и др. Одним из эффективных методов контроля и диагностики при обучении математике считается метод тестирования. Тест как метод изучения индивидуальных различий возник сравнительно недавно. Ввели его в конце XIX и начале XX веков психологи для определения физических, физиологических и психических особенностей человека. Актуальность использования тестов определяется общей задачей оптимизации учебного процесса в условиях школы, современным подходом к ГИА. В обучении геометрии тестирование является одним из эффективных и рациональных дополнений к методам проверки знаний, умений и навыков учащихся. Тесты (в переводе с английского «тест» означает измерение) – универсальный инструмент, с помощью которого измеряется степень овладения умениями и навыками учащихся, определяется уровень усвоения ими ключевых понятий, тем, разделов учебной программы и вполне соответствует принципу самостоятельности в работе ученика и является одним из средств индивидуализации в учебном процессе. Одним из важных достоинств тестов является то, что они предоставляют равные возможности (единая процедура проведения, единые критерии оценки) для всех учащихся. Однако и у них есть свои недостатки, заключающиеся в отсутствии информации о ходе размышлений ученика и скорости его мышления. Несмотря на все достоинства и недостатки использование тестов в учебном процессе показывает, что систематический учет знаний в сочетании с традиционными формами контроля значительно активизирует умственную деятельность учащихся, повышает их культуру логических рассуждений и письменных вычислений. Особую актуальность приобретают тесты по геометрии, использование которых является одним из инструментов управления учебным процессом, позволяя определить достижение каждого учащегося обязательного уровня овладения учебным материалом, а также его готовности к дальнейшему изучению последующих разделов программы по геометрии. При составлении заданий теста по геометрии учителю следует соблюдать ряд рекомендаций: - чёткое определение целей тестирования (т.е. какие знания мы хотим проверить у учащихся: факты, термины, понятия, определения, формулы, теорию; умения применять все это при решении задач и т.д.); - определение вида контроля (входной, промежуточный, тематический, рубежный, итоговый); - выбор формы тестового задания, который зависит от целей тестирования и содержания (закрытая и открытая); - тест должен включать только точные формулировки, ранее изученного материала учебника; - задания теста должны быть сформулированы четко и понятно для учащихся (следует избегать таких слов как «иногда», «часто», «обычно» в правильных утверждениях и слов «всегда», «иногда», «невозможно» в неправильных); - ни одно задание теста не должно служить подсказкой для ответа на другое; - варианты ответов на каждое задание должны подбираться таким образом, чтобы максимально исключить возможность простой догадки; - важно использовать разнообразные формы ответов на задания (например, дополнить, вписать, заполнить, закончить; упорядочить по величине; установить соответствия; установить правильную их последовательность; определить истинность (ложность) утверждений); - задачи для тестов должны быть не слишком громоздкими или слишком простыми; - вариантов ответов на задачу должно быть не менее четырех; - подборка вариантов ответа должна осуществляться с учетом анализа типичных ошибок, допущенных учащимися ранее при изучении данной темы; - правильные ответы заданий должны распределяться в случайном порядке (чтобы учащиеся не могли выявить закономерность правильных ответов); - время, отведенное на выполнение заданий, должно соответствовать уровню их сложности; - каждое задание должно быть пронумеровано в соответствии с уровнем его сложности (чем выше порядковый номер, тем сложнее задание); - тестовые задания должны быть представлены разными уровнями сложности (например: А, B, С), причем в каждом уровне степень их сложности должна быть одинакова. Уровень А – задания, рассчитанные на усвоение основных понятий, на простое отображение материала, на уровне узнаваемости и воспроизведения. Уровень В – задания, требующие размышления, охватывают малый материал, выявляют умения применять знания в стандартных ситуациях. Уровень С – задания, требующие творческого исполнения приобретенных знаний и позволяют выявить умения, применять знания в нестандартных ситуациях; - тесты должны включать задания творческого характера, направленные на развитие творческих способностей учащихся; - важным элементом тестовых заданий является инструкция, текст задания и ключ (ответ который находится у учителя). Учитель при составлении тестов всегда должен четко знать цель тестирования, форму тестового задания в зависимости от целей тестирования и содержания; находить оптимальное время для его проведения. На сегодняшний момент у учителя есть право выбора воспользоваться либо уже готовыми тестами, либо разработать свои собственные. Последние в свою очередь имеют больше преимуществ по сравнению с первыми, поскольку при их составлении могут учитываться индивидуальные особенности класса и возраст учащихся, уровень изучения геометрии (базовый, углубленный), время проведения теста и т.д. Этот метод позволяет представить результаты в форме, максимально отвечающей требованиям согласованности, объективности, надежности и взаимности. Кроме того, тесты как система оценки школьной успеваемости позволяют обеспечить оперативность проверки выполненной работы, сэкономить учебное время, затрачиваемое на опрос. В научно-методической литературе приводится классификация тестов в зависимости от выбранного основания, цели проверки и формы ответов. В документе приводятся примеры многовариантных тематических тестов, которые можно использовать на уроках комплексного применения знаний, проверки, коррекции и оценки знаний в 7-9 классах.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
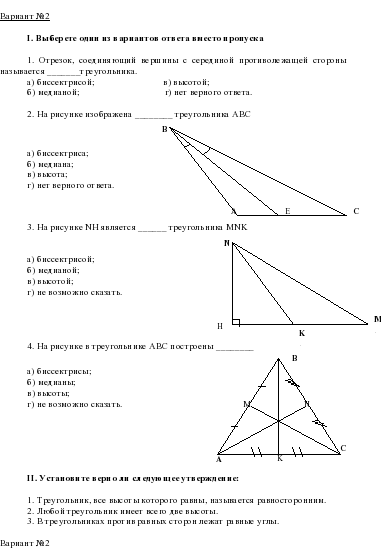
Разноуровневые тесты в обучении решению геометрических задач
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Разноуровневые тесты в обучении решению геометрических задач»
Автор: Ресиме Зариповна Ильязова , Алевтина Николаевна Деева
Дата: 05.09.2016
Номер свидетельства: 342343
Похожие файлы
Полезное для учителя
Распродажа видеоуроков!
1740 руб.
2480 руб.
2020 руб.
2880 руб.
2000 руб.
2860 руб.
2220 руб.
3170 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
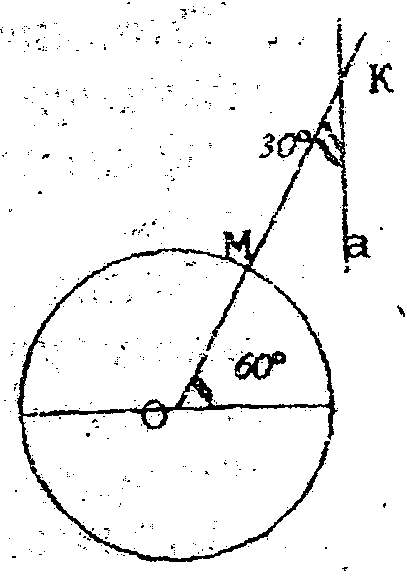 Рис.1
Рис.1  Чему равен радиус окружности?
Чему равен радиус окружности?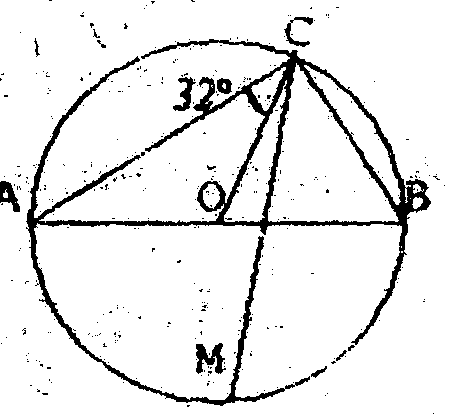 Рис.2
Рис.2 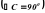 вписан
вписан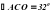 . Чему равен угол ВМС
. Чему равен угол ВМС 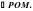
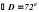 , а величины углов А,В и С относятся как 2 :К:3.
, а величины углов А,В и С относятся как 2 :К:3.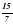 ; б) 3; в)
; б) 3; в) 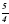 ; г) 1080.
; г) 1080.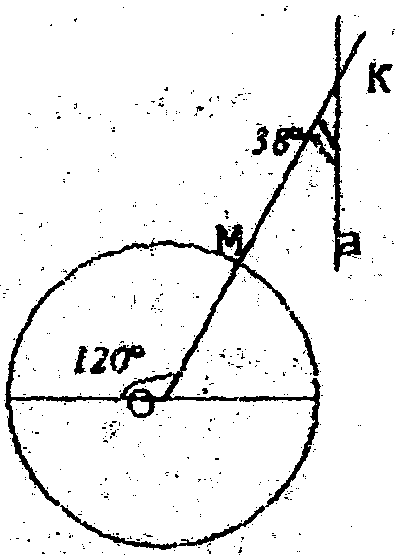 Рис.3
Рис.3 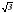 см, проведены к ней две взаимно перпендикулярные касательные. Чему равно расстояние между точками касания?
см, проведены к ней две взаимно перпендикулярные касательные. Чему равно расстояние между точками касания?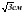 ; б)
; б) 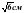 ; в)
; в) 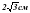 ; г) 6 см.
; г) 6 см. 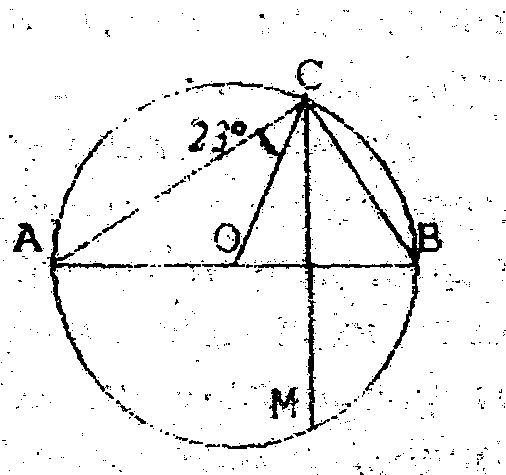 Рис.4
Рис.4 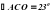 . Чему равен угол ВМС
. Чему равен угол ВМС 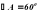 , а величины углов В,С и D относятся как 1:К : 2. Чему должно быть равно К, чтобы около четырёхугольника АВСD можно было описать окружность?
, а величины углов В,С и D относятся как 1:К : 2. Чему должно быть равно К, чтобы около четырёхугольника АВСD можно было описать окружность?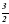 ; б) 2 в) 3; г) 120.
; б) 2 в) 3; г) 120.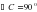 ,точка К
,точка К  - середина медианы СО, проведённой к гипотенузе. Площадь треугольника КВС равна 6м2, а один из катетов равен 8м.Найдите гипотенузу треугольника.
- середина медианы СО, проведённой к гипотенузе. Площадь треугольника КВС равна 6м2, а один из катетов равен 8м.Найдите гипотенузу треугольника.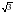 .
.