Данный архив содержит диагностический тест в двух вариантах, который позволяет определить уровень усвоения учащимися темы "Решение линейных неравенств с одной переменной". . Есть необходимый справочный материал, который позволяет учащимся повторить основные правила по данной теме.При выполнении проверочной работы учащиеся могут проверить и оценить свою работу по укзанным правильным ответам. В данном архиве есть самостоятельная работа по теме "Решение линейных неравенств с одной переменной" (6 класс), которую проверяет учитель. Есть задания углубленного и продвинутого уровня.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Линейные неравенства (6 класс, технология полного усвоения)
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«®¢â®àë© ã஢¥ì, ¯à®¤¢¨ãâë© ã஢¥ì, 㣫㡫¥ë© ã஢¥ì»
Полезное для учителя
Распродажа видеоуроков!
1720 руб.
2860 руб.
1060 руб.
1760 руб.
1690 руб.
2820 руб.
1690 руб.
2820 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
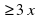 .
.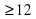
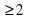

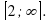
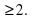
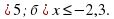



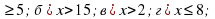
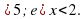
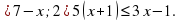
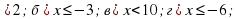
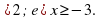
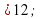
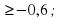
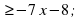
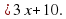
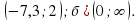
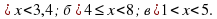
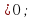
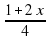
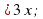
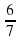 - 3х
- 3х 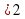 .
.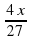 –
– 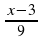 +
+ 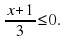
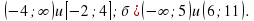
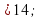 б) х –
б) х –  +
+ 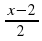
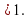
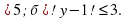
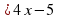 не имеет решения (при положительном ответе укажите это значение)?
не имеет решения (при положительном ответе укажите это значение)?















