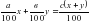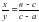На первом этапе основной школы на изучение темы «Проценты» отводится непродолжительное время. В это время учащиеся в силу возрастных особенностей ещё не могут получить полноценные представления о процентах, об их роли в повседневной жизни. На последующих этапах обучения повторного обращения к этой теме не предусматривается. В учебниках встречаются задачи на проценты, но в них отсутствует компактное и чёткое изложение вопроса. Текстовые задачи включены в материал итоговой аттестации за курс основной и полной средней школы. Однако задачи на проценты вызывают затруднения у учащихся, многие из них не имеют прочных навыков обращения с процентами в повседневной жизни.
Создайте Ваш сайт учителя Видеоуроки Олимпиады Вебинары для учителей
Занимательный материал как средство развития УУД на уроках математики
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Занимательный материал как средство развития УУД на уроках математики»
Полезное для учителя
Распродажа видеоуроков!
1540 руб.
2560 руб.
1900 руб.
3170 руб.
1690 руб.
2820 руб.
1800 руб.
3000 руб.
ПОЛУЧИТЕ СВИДЕТЕЛЬСТВО МГНОВЕННО
* Свидетельство о публикации выдается БЕСПЛАТНО, СРАЗУ же после добавления Вами Вашей работы на сайт
Удобный поиск материалов для учителей
Проверка свидетельства
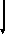


 вода
вода
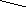
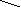
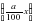 (г), у(г) –
(г), у(г) – 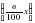 (г).
(г).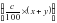 , где acесли cв или ca, то задача неразрешима.
, где acесли cв или ca, то задача неразрешима.