Максимальное количество баллов, которое может получить экзаменуемый за выполнение всей экзаменационной работы, – 32 баллов. Из них – за модуль «Алгебра» – 14 баллов, за модуль «Геометрия» – 11 баллов, за модуль «Реальная математика» – 7 баллов.
Рекомендуемый минимальный результат выполнения экзаменационной работы, свидетельствующий об освоении федерального компонента образовательного стандарта в предметной области «Математика», – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика». Преодоление этого минимального результата даёт выпускнику право на получение, в соответствии с учебным планом образовательного учреждения, итоговой отметки по математике или по алгебре и геометрии.
Рекомендованные шкалы пересчёта первичного балла в экзаменационную отметку по пятибалльной шкале:
суммарного балла за выполнение работы в целом - в экзаменационную отметку по математике (табл. 2);
суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» (все задания модуля «Алгебра» и задания 14, 15, 16, 18, 19, 20 модуля «Реальная математика»), - в экзаменационную отметку по алгебре (табл. 3);
суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» (все задания модуля «Геометрия» и задание 17 модуля «Реальная математика»), - в экзаменационную отметку по геометрии (табл. 4).
Таблица 2
Шкала пересчета суммарного балла за выполнение экзаменационной работы в целом в отметку по математике
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Суммарный балл за работу в целом | 0 - 7 | 8 - 14 | 15 - 21 | 22 - 32 |
Таблица 3
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» в отметку по алгебре
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Суммарный балл по алгебраическим заданиям | 0 - 4 | 5 - 10 | 11 - 15 | 16 - 20 |
Таблица 4
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» в отметку по геометрии
| Отметка по пятибалльной шкале | «2» | «3» | «4» | «5» |
| Суммарный балл по геометрическим заданиям | 0 - 2 | 3 - 4 | 5 - 7 | 8 - 12 |
Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:
для естественнонаучного профиля: 18 баллам, из них не менее 10 по алгебре, и не менее 6 по геометрии;
для экономического профиля: 18 баллам, из них не менее 9 по алгебре, 3 по геометрии, 5 по реальной математике;
для физико-математического профиля: 19 баллам, из них не менее 11 по алгебре, 7 по геометрии.
Ответы к тренировочной работе по математике в 9 классе 5.11.2015 год
Часть 1
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 1вариант | 0,5 | 2 | 1 | 8 | 3 | 5,8 | 0 | 2 | 155 | 15 | 42 | 0,75 | 13 | 2 | 1 | 48125000 | 20 | 2 | 0,7 | 260 |
| 2 вариант | 7 | 4 | 2 | 6 | 2 | 8,3 | 706,4 | 3 | 118 | 44 | 8 | 4 | 1 | 2 | 4 | 50625000 | 8 | 3 | 0,1 | 0,88 |
| 3 вариант | 1,5 | 2 | 1 | 5 | 4 | 11 | 0,64 | 4 | 129 | 52 | 30 | 1,5 | 3 | 2 | 12 | 25000000 | 40 | 3 | 0,4 | 315 |
| 4 вариант | 1,8 | 3 | 2 | 7 | 2 | 10,6 | -498,4 | 4 | 105 | 61 | 32 | 5 | 23 | 2 | 20 | 11250000 | 30 | 14 | 0,76 | 18 |
| 5 вариант | 2 | 2 | 3 | 7 | 1 | 4,4 | 24 | 1 | 157 | 36 | 192 | 0,6 | 13 | 3 | 20 | 48000000 | 36 | 3 | 0,2 | 0,72 |
Часть 2
Задание 21

Задание 22

Задание 23

Задание 24

Задание 25

Задание 26

Вариант 1
Задание 21. Один из корней уравнения 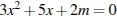 равен
равен 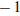 . Найдите второй корень.
. Найдите второй корень.
Решение.
Подставим известный корень в уравнение:  . Получим уравнение относительно
. Получим уравнение относительно 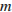 . Решим его:
. Решим его:  . Подставим
. Подставим 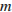 уравнение:
уравнение:  , откуда
, откуда

Ответ: 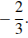
Задание 22. На изготовление 231 детали ученик тратит на 11 часов больше, чем мастер на изготовление 462 таких же деталей. Известно, что ученик за час делает на 4 детали меньше, чем мастер. Сколько деталей в час делает ученик?
Решение.
Предположим, что ученик делает  деталей в час. Тогда мастер делает
деталей в час. Тогда мастер делает 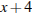 детали в час.
детали в час.
На изготовление 231 детали ученик потратит  ч, а мастер тратит
ч, а мастер тратит  ч на изготовление 462 деталей.
ч на изготовление 462 деталей.
Составим уравнение по условию задачи:
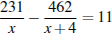 .
.
Решим уравнение:
 .
.
Корни полученного квадратного уравнения: −28 и 3. Отбрасывая отрицательный корень, находим, что ученик делает в час 3 детали.
Ответ: 3.
Задание 23 . Парабола проходит через точки K(0; –5), L(3; 10), M( –3; –2). Найдите координаты её вершины.
Решение.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 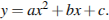 Координата
Координата  вершины параболы находится по формуле
вершины параболы находится по формуле 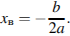 Координату
Координату  вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 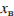 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов  и
и  Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
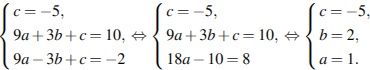
Найдём координаты вершины:
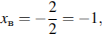
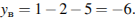
Ответ: (−1; −6).
Задание 24. В треугольнике 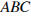 угол
угол 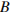 равен 72°, угол
равен 72°, угол  равен 63°,
равен 63°, 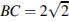 . Найдите радиус описанной около этого треугольника окружности.
. Найдите радиус описанной около этого треугольника окружности.
Решение.
Угол  треугольника
треугольника 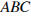 равен
равен 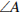 = 180° −
= 180° − 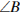 −
−  = 45°.
= 45°.
Радиус описанной окружности равен 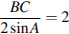 .
.
Ответ: 2.
Задание 25. Докажите, что у равных треугольников 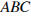 и
и 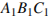 биссектрисы, проведённые из вершины
биссектрисы, проведённые из вершины 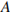 и
и 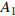 , равны.
, равны.
Решение.
Пусть 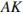 и
и 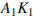 — биссектрисы треугольников
— биссектрисы треугольников 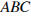 и
и 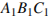 . В треугольниках
. В треугольниках 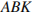 и
и  соответственно равны стороны
соответственно равны стороны  и
и  , а также углы
, а также углы  и
и  ,
,  и
и  . Следовательно, треугольники равны по второму признаку равенства треугольников. Значит, , что и требовалось доказать.
. Следовательно, треугольники равны по второму признаку равенства треугольников. Значит, , что и требовалось доказать.
Задание 26. Площадь треугольника ABC равна 80. Биссектриса AD пересекает медиану BK в точке E, при этом BD:CD=1:3. Найдите площадь четырехугольника EDCK.
Решение.
Пусть AK=KC=3x, тогда AB=2x, так как по свойству биссектрисы. Значит,
Пусть S - площадь треугольника ABC, тогда
Таким образом,
Ответ: 36.
Вариант 2
Задание 21. Решите уравнение:
Решение.
Раскладывая на множители левую часть уравнения, получаем Таким образом, корни уравнения
Ответ: 
Задание 22. Чтобы накачать в бак 117 л воды, требуется на 5 минут больше времени, чем на то, чтобы выкачать из него 96 л воды. За одну минуту можно выкачать на 3 л воды больше, чем накачать. Сколько литров воды накачивается в бак за минуту?
Решение.
Пусть за минуту в бак накачивается  литров воды. Тогда за минуту выкачивается
литров воды. Тогда за минуту выкачивается  л воды.
л воды.
По условию задачи составим уравнение:
,откуда
Получаем квадратное уравнение
,имеющее корни:  и
и  .
.
Отбрасывая отрицательный корень, находим, что за минуту в бак накачивается 9 л воды.
Ответ: 9.
Задание 23. Парабола проходит через точки A(0; 6), B(6; –6), C(1; 9). Найдите координаты её вершины.
Решение.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 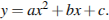 Координата
Координата  вершины параболы находится по формуле
вершины параболы находится по формуле 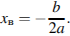 Координату
Координату  вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 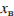 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов  и
и  Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Ответ: (2; 10).
Задание 24 Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.
Решение.
Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:
откуда 
Ответ: 16.
Задание 25. Докажите, что биссектрисы углов при основании равнобедренного треугольника равны.
Решение.
Имеем:
Докажем, что  .
.
1) по стороне и двум прилежащим к ней углам:
а)  — общая;
— общая;
б) по свойству углов равнобедренного треугольника;
в) по определению биссектрисы и равенству углов при основании равнобедренного треугольника.
2)  как соответствующие элементы равных треугольников.
как соответствующие элементы равных треугольников.
Задание 26. Боковые стороны AB и CD трапеции ABCD равны соответственно 20 и 25, а основание BCравно 5. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
Решение.
Введём обозначения как показано на рисунке. Продолжим биссектрису до пересечения с прямой  в точке
в точке  Углы
Углы  и
и  равны как накрест лежащие при параллельных прямых. Значит, следовательно, треугольник
равны как накрест лежащие при параллельных прямых. Значит, следовательно, треугольник  — равнобедренный: Найдём Углы
— равнобедренный: Найдём Углы  и
и  равны как вертикальные. Рассмотрим треугольники
равны как вертикальные. Рассмотрим треугольники  и
и  стороны
стороны  и
и  равны, углы
равны, углы  и
и  равны как вертикальные, углы
равны как вертикальные, углы  и
и  равны как накрест лежащие при параллельных прямых, следовательно, эти треугольники равны, откуда Проведём прямую
равны как накрест лежащие при параллельных прямых, следовательно, эти треугольники равны, откуда Проведём прямую  параллельную
параллельную  Прямая
Прямая  параллельна
параллельна  прямая
прямая  параллельна
параллельна  следовательно, четырёхугольник
следовательно, четырёхугольник  — параллелограмм, откуда Найдём Рассмотрим треугольник
— параллелограмм, откуда Найдём Рассмотрим треугольник  заметим, что
заметим, что
Следовательно, по теореме, обратной теореме Пифагора, получаем, что треугольник  — прямоугольный, следовательно,
— прямоугольный, следовательно,  — высота трапеции. Найдём площадь трапеции:
— высота трапеции. Найдём площадь трапеции:
Ответ: 250.
Вариант 3
Задание 21. Решите уравнение:
Решение.
Сделаем замену  Получаем уравнение
Получаем уравнение
Корни: 
Если  , то
, то  или
или 
Если  , то
, то  или
или 
Ответ: 
Задание 22. Дима и Саша выполняют одинаковый тест. Дима отвечает за час на 12 вопросов теста, а Саша — на 22. Они одновременно начали отвечать на вопросы теста, и Дима закончил свой тест позже Саши на 75 минут. Сколько вопросов содержит тест?
Решение.
Пусть x — количество вопросов теста через. Тогда получаем:
откуда находим x = 33 .
Ответ: 33
Задание 23. Парабола проходит через точки K(0; –2), L(4; 6), M(1; 3). Найдите координаты её вершины.
Решение.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 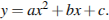 Координата
Координата  вершины параболы находится по формуле
вершины параболы находится по формуле 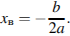 Координату
Координату  вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 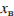 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов  и
и  Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Ответ: (3; 7).
Задание 24. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B . Найдите диаметр окружности, если AB =15, AC = 25.
Решение.
Пусть DC = x. Тогда по свойству касательной и секущей, проведённых из одной точки к окружности, получаем:
AB2 = AC(AC − x); 225 = 25(25 − x), откуда x = 16.
Ответ: 16.
Задание 25. На медиане KF треугольника MKP отмечена точка E. Докажите, что если EM = EP, то KM = KP.
Решение.
Поскольку треугольник  — равнобедренный, получаем, что его медиана
— равнобедренный, получаем, что его медиана  также является высотой. Значит, в треугольнике
также является высотой. Значит, в треугольнике  отрезок
отрезок  является высотой и медианой. Поэтому треугольник
является высотой и медианой. Поэтому треугольник  — равнобедренный, то есть
— равнобедренный, то есть  .
.
Задание 26. Основания трапеции относятся как 1:3. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. В каком отношении эта прямая делит площадь трапеции?
Решение.
Введём обозначения как показано на рисунке. Отрезок, проходящий через точку пересечения диагоналей трапеции, равен среднему гармоническому её оснований. Пусть  тогда
тогда  и Поскольку треугольники
и Поскольку треугольники  и
и  подобны, их высоты
подобны, их высоты  и
и  , проведенные соответственно к сторонам
, проведенные соответственно к сторонам  и
и  относятся как 3:1. Тем самым, для отношения искомого отношения площадей трапеций
относятся как 3:1. Тем самым, для отношения искомого отношения площадей трапеций  и
и  имеем:
имеем:
Ответ: 5:27.
Вариант 4
Задание 21. Решите уравнение: 
Решение.
Перенесем все члены в левую часть и разложим ее на множители:
 при всех значениях
при всех значениях  поэтому
поэтому  Значит,
Значит, 
Ответ: 1.
Задание 22. Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?
Решение.
Пусть вторая труба пропускает  литров воды в минуту, тогда первая труба пропускает
литров воды в минуту, тогда первая труба пропускает  литра в минуту. Вторая труба заполняет резервуар объёмом 130 литров за
литра в минуту. Вторая труба заполняет резервуар объёмом 130 литров за  минут. Поскольку первая труба заполняет резервуар объёмом 136 литров за
минут. Поскольку первая труба заполняет резервуар объёмом 136 литров за  минут, что по условию задачи на 4 минуты больше, чем
минут, что по условию задачи на 4 минуты больше, чем  получаем уравнение:
получаем уравнение:
Решим уравнение:
 или
или 
Отбрасывая постороннее решение −6,5, получаем, что вторая труба пропускает 10 литров в минуту.
Ответ: 10 литров в минуту.
Задание 23. Парабола проходит через точки K(0; 2), L( – 5; – 3), M(1; 9). Найдите координаты её вершины.
Решение.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 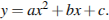 Координата
Координата  вершины параболы находится по формуле
вершины параболы находится по формуле 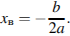 Координату
Координату  вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 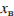 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов  и
и  Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Ответ: (−3; −7).
Задание 24. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7,5, а AB = 2.
Решение.
Введём обозначения как показано на рисунке. Радиус окружности, проведённый в точку касания перпендикулярен касательной, поэтому треугольник  — прямоугольный. Найдём
— прямоугольный. Найдём  по теореме Пифагора:
по теореме Пифагора:
Следовательно, длина стороны  равна
равна
Ответ: 8.
Задание 25. На стороне АС треугольника АВС отмечены точки D и E так, что AD = CE. Докажите, что если BD = BE , то АВ = ВС.
Решение.Треугольник  — равнобедренный, поэтому . Значит, и треугольники
— равнобедренный, поэтому . Значит, и треугольники  и
и  равны по первому признаку равенства треугольников. Значит,
равны по первому признаку равенства треугольников. Значит,  .
.
Задание 26. Высота AH ромба ABCD делит сторону CD на отрезки DH = 21 и CH = 8. Найдите высоту ромба.
Решение.
Введём обозначения как показано на рисунке. Угол  и
и  равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники
равны как углы с взаимно перпендикулярными сторонами. Рассмотрим треугольники  и
и  они прямоугольные, углы
они прямоугольные, углы  и
и  равны, следовательно, эти треугольники подобны, откуда Диагонали ромба делятся точкой пересечения пополам: Получаем:
равны, следовательно, эти треугольники подобны, откуда Диагонали ромба делятся точкой пересечения пополам: Получаем:
Из прямоугольного треугольника  используя теорему Пифагора найдём
используя теорему Пифагора найдём 
Ответ: 20.
-----------
Приведем другое решение:
Вариант 5
Задание 21. Решите уравнение
Решение.
Преобразуем уравнение:
Ответ: −4; −3; 3.
Задание 22. Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение.
Пусть  — число деталей, изготавливаемых первым рабочим за час, тогда
— число деталей, изготавливаемых первым рабочим за час, тогда  — число деталей, изготавливаемых вторым рабочим за час. Заказ, состоящий из 60 деталей первый рабочий выполняет на 3 часа быстрее, чем второй, составим уравнение:
— число деталей, изготавливаемых вторым рабочим за час. Заказ, состоящий из 60 деталей первый рабочий выполняет на 3 часа быстрее, чем второй, составим уравнение:
Корень −10 не подходит по условию задачи, следовательно, первый рабочий изготавливает 20 деталей в час. Значит, второй рабочий изготавливает 10 деталей в час.
Ответ: 10.
Задание 23. Парабола проходит через точки A(0; – 6), B( – 5; – 1), C(1; – 1). Найдите координаты её вершины.
Решение.
Одна из возможных форм записи уравнения параболы в общем виде выглядит так: 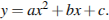 Координата
Координата  вершины параболы находится по формуле
вершины параболы находится по формуле 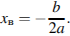 Координату
Координату  вершины параболы найдётся подстановкой
вершины параболы найдётся подстановкой 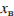 в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов
в уравнение параболы. Таким образом, задача сводится к нахождению коэффициентов  и
и  Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Подставив координаты точек, через которые проходит парабола, в уравнение параболы и получим систему из трёх уравнений:
Найдём координаты вершины:
Ответ: (−2; −10).
Задание 24. В треугольнике ABC угол С равен 90°, радиус вписанной окружности равен 2. Найдите площадь треугольника ABC, если AB = 12.
Решение.
Пусть A1, B1 и C1 — точки касания вписанной окружности со сторонами BC, AC и AB соответственно. Радиус вписанной окружности обозначим r. Тогда AC1 = AB1 и CA1 = CB1 = r. Периметр треугольника ABC равен 2AC1 + 2BC1 + 2CA1 = 2AB + 2r. Полупериметр p равен AB + r.
По формуле площади треугольника находим
Ответ: 28.
Задание 25. В равностороннем треугольнике ABC точки M, N, K — середины сторонАВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
Решение.
Так как точки M, N, K - середины сторон и треугольник ABC- равносторонний, то отрезки AM, MB, BN, NC, KC, AK равны. В равностороннем треугольнике все углы равны, таким образом, треугольники AMK, NMB, CNK равны по двум сторонам и углу между ними. Тогда MN=MK=KN, значит треугольник MNK- равносторонний.
Задание 26. Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB иCD в точках E и F соответственно. Найдите длину отрезка EF, если AD = 42, BC = 14, CF:DF = 4:3.
Решение.
Проведём построения и введём обозначения как показано на рисунке. Рассмотрим треугольники  и
и  угол C — общий, углы
угол C — общий, углы  и
и  равны друг другу как соответственные углы при параллельных прямых, следовательно, треугольники
равны друг другу как соответственные углы при параллельных прямых, следовательно, треугольники  и
и  подобны. Откуда поэтому Аналогично, из треугольников
подобны. Откуда поэтому Аналогично, из треугольников  и
и 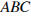 получаем, что Таким образом, Ответ: 30.
получаем, что Таким образом, Ответ: 30.

 2) 4
2) 4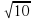 3) 12 4) 2
3) 12 4) 2
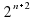 2)
2) 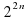 3)
3) 4)
4) 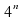






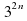 2)
2) 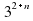 3)
3) 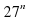 4)
4) 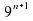






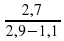
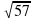
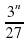 ?
?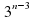 2)
2) 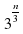 3)
3)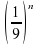 4)
4) 
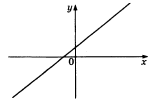
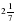
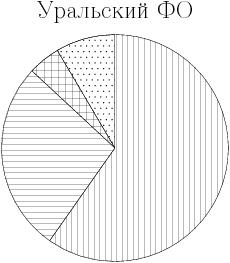
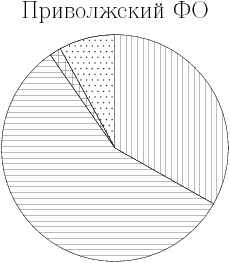



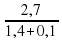
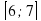 ?
?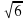 2)
2) 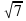 3)
3)  4)
4) 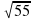
 ?
?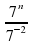 2)
2)  3)
3) 4)
4) 




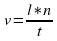 , где
, где 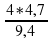
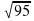 ?
?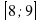 2)
2) 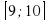 3)
3) 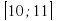 4)
4) 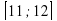
 ?
? 2)
2)  3)
3)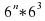 4)
4)